SM "Kurovskaja keskkool nr 6"

MATEMAATIKA KOKKUVÕTE TEEMAL:

« EBATAVAD KORRUTUSVIISID».

Lõpetanud 6 "b" klassi õpilane

Krestnikov Vassili.

Juhendaja:

Smirnova Tatjana Vladimirovna

Sissejuhatus…………………………………………………………………………2

Põhiosa. Ebatavalised viisid korrutamine……………………………3

2.1. Natuke ajalugu…………………………………………………………………..3

2.2. Korrutamine sõrmedel…………………………………………………………………4

2.3. Korrutamine 9-ga…………………………………………………………………………5

2.4. India korrutamisviis ………………………………………………….6

2.5. Korrutamine “väikese lossi” meetodil………………………………………………………7

2.6. Korrutamine “armukadeduse” meetodil…………………………………………………8

2.7. Talupoeglik korrutamisviis………………………………………………..9

2.8 Uus viis……………………………………………………………………..10

Järeldus…………………………………………………………………………… 11

Viited……………………………………………………………….1 2

I. Sissejuhatus.

Inimesel on igapäevaelus võimatu ilma arvutusteta hakkama saada. Seetõttu õpetatakse meid matemaatikatundides ennekõike arvudega tehteid sooritama ehk loendama. Korrutame, jagame, liidame ja lahutame kõigile koolis õpitavatele tavapärastel viisidel.

Kord sattusin juhuslikult S. N. Olehnika, Yu. V. Nesterenko ja M. K. Potapovi raamatule "Vanad meelelahutuslikud probleemid". Seda raamatut lehitsedes tõmbas mu tähelepanu lehekülg nimega "Korrutamine sõrmedel". Selgus, et korrutada saab mitte ainult nii, nagu nad meile matemaatikaõpikutes pakuvad. Mõtlesin, kas on veel mingeid arvutamise viise. Lõppude lõpuks on kiire arvutuste tegemise võimalus ausalt öeldes üllatav.

Kaasaegse pidev kasutamine arvutiteadus toob kaasa asjaolu, et õpilastel on raske teha arvutusi ilma tabelite või arvutusmasinata. Lihtsustatud arvutustehnikate tundmine võimaldab mitte ainult peas kiiresti teha lihtsaid arvutusi, vaid ka mehhaniseeritud arvutuste tulemusena kontrollida, hinnata, leida ja parandada vigu. Lisaks arendab arvutusoskuste arendamine mälu, tõstab matemaatilise mõtlemiskultuuri taset, aitab täielikult assimileerida füüsilise ja matemaatilise tsükli aineid.

Eesmärk:

Näita ebatavalistkorrutamismeetodid.

Ülesanded:

Otsige üles nii palju kui võimalikebatavalised arvutusviisid.

Õppige neid rakendama.

Valige enda jaoks kõige huvitavam või lihtsam kui needpakutudkoolis ja kasutage neid loendamisel.

II. Põhiosa. Ebatavalised korrutamisviisid.

2.1. Natuke ajalugu.

Praegu kasutatavad arvutusmeetodid ei olnud alati nii lihtsad ja mugavad. Vanasti kasutati tülikamaid ja aeglasemaid meetodeid. Ja kui 21. sajandi koolipoiss saaks reisida viis sajandit tagasi, avaldaks ta meie esivanematele muljet oma arvutuste kiiruse ja täpsusega. Kuulujutt temast oleks levinud ümberkaudsetes koolides ja kloostrites, varjutades tolle ajastu osavamate lettide hiilguse ja uue suure meistri juurde oleks tulnud kõikjalt õppima.

Eriti rasked olid vanasti korrutamise ja jagamise toimingud. Sel ajal ei olnud iga tegevuse jaoks välja töötatud ühte tehnikat. Vastupidi, korraga oli kasutusel ligi kümmekond erinevat korrutamis- ja jagamismeetodit – üks keerulisem kui teine, mida keskmise võimekusega inimene ei mäletanudki. Iga arvutamise õpetaja hoidis kinni oma lemmikmeetodist, iga "jagamismeister" (oli selliseid spetsialiste) kiitis oma viisi selle toimingu sooritamiseks.

V. Bellyustini raamatus “Kuidas inimesed järk-järgult jõudsid tõelise aritmeetikani” on välja toodud 27 korrutamismeetodit ja autor märgib: “On täiesti võimalik, et raamatuhoidlate süvendites on peidus rohkem meetodeid, mis on hajutatud paljudes , peamiselt käsitsi kirjutatud kogud.

Ja kõik need korrutamismeetodid - "male või orel", "painutamine", "rist", "võre", "tagasi ette", "teemant" jt võistlesid omavahel ja assimileeriti suurte raskustega.

Vaatame kõige huvitavamaid ja lihtsamaid korrutamisviise.

2.2. Sõrmede korrutamine.

Vana-Vene meetod sõrmedel korrutamiseks on üks levinumaid meetodeid, mida vene kaupmehed on edukalt kasutanud juba mitu sajandit. Õpiti sõrmedel korrutama ühekohalisi numbreid 6-st 9-ni. Samas piisas ka näpulugemise algoskustest “ühes”, “paaris”, “kolmiks”, “neljas”, “ viiesed” ja “kümned”. Sõrmed toimisid siin abistava arvutusseadmena.

Selleks sirutasid nad ühelt poolt nii palju sõrmi, kuivõrd esimene tegur ületab arvu 5, ja teiselt poolt tegid nad sama teise teguri puhul. Ülejäänud sõrmed olid kõverdatud. Seejärel võeti väljasirutatud sõrmede arv (kokku) ja korrutati 10-ga, seejärel korrutati numbrid, mis näitavad, mitu sõrme oli kätel kõverdatud, ja liideti tulemused.

Näiteks korrutame 7 8-ga. Vaadeldavas näites painutatakse 2 ja 3 sõrme. Kui liita kokku painutatud sõrmede arv (2+3=5) ja korrutada painutamata sõrmede arv (2 3=6), siis saame soovitud korrutise kümnendite ja ühikute arvud vastavalt 56 . Nii saate arvutada kõigi ühekohaliste arvude korrutise, mis on suuremad kui 5.

2.3. Korrutage 9-ga.

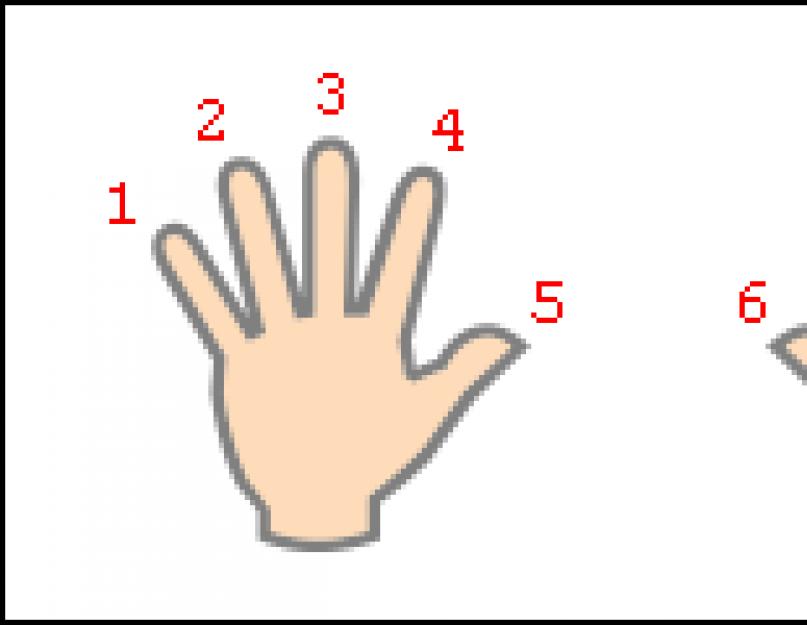
Arvu 9 korrutamine- 9 1, 9 2 ... 9 10 - on lihtsam mälust kustutada ja käsitsi liitmise teel keerulisem ümber arvutada, kuid just numbri 9 puhul on korrutamine hõlpsasti reprodutseeritav "sõrmedel". Siruta sõrmed mõlemale käele laiali ja keera peopesad endast eemale. Määrake vaimselt sõrmedele järjestuses numbrid vahemikus 1 kuni 10, alustades vasaku käe väikesest sõrmest ja lõpetades väikese sõrmega parem käsi(see on näidatud joonisel).

Oletame, et tahame 9 korrutada 6-ga. Painutame sõrme, mille arv on võrdne arvuga, millega üheksa korrutame. Meie näites peate painutama sõrme numbriga 6. Painutatud sõrmest vasakul olevate sõrmede arv näitab meile vastuses kümnete arvu, paremal olevate sõrmede arvu - ühtede arvu. Vasakul on 5 sõrme painutamata, paremal - 4 sõrme. Seega 9 6=54. Allolev joonis näitab üksikasjalikult kogu "arvutamise" põhimõtet.

Teine näide: peate arvutama 9 8=?. Teel ütleme, et sõrmed ei pruugi tingimata toimida "arvutusmasinana". Võtke näiteks märkmikus 10 lahtrit. Tõmbame 8. lahtri maha. Vasakul on 7 lahtrit, paremal 2 lahtrit. Seega 9 8=72. Kõik on väga lihtne.

7 rakku 2 rakku.

2.4. India korrutamise viis.

Kõige väärtuslikum panus matemaatiliste teadmiste varakambrisse anti Indias. Hindud pakkusid välja viisi, kuidas me kasutame arvude kirjutamiseks kümmet märki: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Selle meetodi aluseks on idee, et sama number tähistab ühikuid, kümneid, sadu või tuhandeid, olenevalt sellest, kus see arv asub. Numbrite puudumisel määratakse hõivatud koht numbritele määratud nullidega.

Indiaanlased arvasid hästi. Nad mõtlesid välja väga lihtsa viisi korrutamiseks. Nad sooritasid korrutamise, alustades kõrgeimast järjekorrast, ja kirjutasid mittetäielikud korrutised üles korrutise kohale, osade kaupa. Samas oli kohe näha ka terviktoote vanem number ja lisaks oli välistatud ühegi numbri ärajätmine. Korrutamismärki polnud veel teada, mistõttu jätsid nad tegurite vahele väikese vahemaa. Näiteks korrutame need viisil 537 6-ga:

(5 ∙ 6 =30) 30

(300 + 3 ∙ 6 = 318) 318

(3180 +7 ∙ 6 = 3222) 3222

2.5 . korrutamise viis"VÄIKE LOSSI".

Nüüd õpitakse kooli esimeses klassis arvude korrutamist. Kuid keskajal valdasid korrutamise kunsti väga vähesed. Haruldane aristokraat võis kiidelda korrutustabeli tundmisega, isegi kui ta on lõpetanud mõne Euroopa ülikooli.

Matemaatika arengu aastatuhandete jooksul on leiutatud palju võimalusi arvude korrutamiseks. Itaalia matemaatik Luca Pacioli oma traktaadis "Teadmiste summa aritmeetikas, suhetes ja proportsionaalsuses" (1494) annab kaheksa erinevat korrutamismeetodit. Esimene neist kannab nime "Väike loss", teine ​​aga mitte vähem romantiline nimega "Armukadedus või võrekorrutis".

“Väikese lossi” korrutamismeetodi eeliseks on see, et kõige kõrgemate numbrite numbrid määratakse algusest peale ja see võib olla oluline, kui on vaja väärtust kiiresti hinnata.

Ülemise arvu numbrid, alustades kõige olulisemast numbrist, korrutatakse vaheldumisi alumise numbriga ja kirjutatakse veergu, lisades vajaliku arvu nulle. Seejärel liidetakse tulemused kokku.

2.6. Numbrite korrutaminearmukadeduse meetod.

Teist meetodit nimetatakse romantiliselt "armukadeduseks" või "võrekorrutamiseks".

Kõigepealt joonistatakse ristkülik, mis on jagatud ruutudeks ja ristküliku külgede mõõtmed vastavad kordaja ja kordaja kümnendkohtade arvule. Seejärel jagatakse ruudukujulised lahtrid diagonaalselt ja "... selgub pilt, mis näeb välja nagu võre aknaluugid, rulood," kirjutab Pacioli. "Sellised aknaluugid riputati Veneetsia majade akendele, mis takistasid möödujatel akendel istuvaid daame ja nunnasid näha."

Korrutame sel viisil 347 29. Joonistame tabeli, kirjutame selle kohale arv 347 ja paremale arv 29.

Igal real kirjutame selle lahtri kohale ja sellest paremale arvude korrutise, kaldkriipsu kohale aga korrutise kümnendite arv ja selle alla ühikute arv. Nüüd liidage iga kaldkriipsu numbrid, tehes seda toimingut paremalt vasakule. Kui summa on väiksem kui 10, siis kirjutame selle riba alumise numbri alla. Kui selgub, et see on suurem kui 10, siis kirjutame ainult summa ühikute arvu ja lisame kümnete arvu järgmisele summale. Selle tulemusena saame soovitud toote 10063.

2.7. Tomaalähedane korrutamisviis.

Kõige rohkem on minu meelest "native" ja lihtne viis korrutamine on vene talupoegade meetod. See meetod ei nõua üldjuhul teadmisi korrutustabeli kohta, mis on suurem kui arv 2. Selle olemus seisneb selles, et mis tahes kahe arvu korrutamine taandatakse ühe arvu järjestikusteks jagamisteks pooleks, samal ajal kui teise arvu kahekordistatakse. Poolitamine jätkub, kuni jagatis on 1, samal ajal kahekordistades paralleelselt teist arvu. Viimane kahekordistatud number annab soovitud tulemuse.

Paaritu arvu korral tuleb ühik ära visata ja ülejäänud osa pooleks jagada; kuid teisest küljest tuleb parempoolse veeru viimasele numbrile lisada kõik selle veeru numbrid, mis on vasakpoolse veeru paaritute numbrite vastu: summa on soovitud korrutis

Kõigi vastavate arvupaaride korrutis on sama, seega

37 ∙ 32 = 1184 ∙ 1 = 1184

Kui üks numbritest on paaritu või mõlemad numbrid on paaritud, toimige järgmiselt.

384 ∙ 1 = 384

24 ∙ 17 = 24∙(16+1)=24 ∙ 16 + 24 = 384 + 24 = 408

2.8 . Uus viis paljundamiseks.

huvitav uus korrutamisviis, millest hiljuti teatati. Leiutaja uus süsteem suulisest arvutamisest, filosoofiadoktor Vassili Okoneshnikov väidab, et inimene suudab tohutul hulgal teavet meelde jätta, peaasi, kuidas seda teavet korraldada. Teadlase enda sõnul on üheksa kümnendkoha süsteem selles osas kõige soodsam – kõik andmed on lihtsalt paigutatud üheksasse lahtrisse, mis on paigutatud kalkulaatori nuppudena.

Sellise tabeli järgi on väga lihtne kokku lugeda. Näiteks korrutame arvu 15647 5-ga. Tabeli viiele vastavas osas valime järjekorras numbri numbritele vastavad arvud: üks, viis, kuus, neli ja seitse. Saame: 05 25 30 20 35

Vasakpoolne arv (meie näites null) jäetakse muutmata ja paarikaupa liidetakse järgmised numbrid: viis kahega, viis kolmega, null kahega, null kolmega. Ka viimane number on muutumatu.

Selle tulemusena saame: 078235. Arv 78235 on korrutamise tulemus.

Kui kahe numbri liitmisel saadakse arv, mis ületab üheksat, lisatakse selle esimene number tulemuse eelmisele numbrile ja teine ​​kirjutatakse selle asemele.

III. Järeldus.

Kõigist leitud ebatavalistest loendusmeetoditest tundus kõige huvitavam meetod „võrekorrutamine või armukadedus”. Näitasin seda oma klassikaaslastele ja ka neile meeldis see väga.

Lihtsaim meetod tundus mulle vene talupoegade poolt kasutatav kahekordistamise ja poolitamise meetod. Kasutan seda mitte liiga suurte arvude korrutamisel (kahekohaliste arvude korrutamisel on väga mugav kasutada).

Mind huvitas uus korrutamisviis, sest see võimaldab mõtetes tohutuid numbreid "keerata".

Ma arvan, et ka meie veeruga korrutamise meetod ei ole täiuslik ning me saame välja mõelda veelgi kiiremaid ja usaldusväärsemaid meetodeid.

Kirjandus.

Depman I. "Lugusid matemaatikast". - Leningrad.: Haridus, 1954. - 140 lk.

Korneev A.A. Vene korrutamise fenomen. Lugu. http://numbernautics.ru/

Olehnik S. N., Nesterenko Yu. V., Potapov M. K. "Vanad meelelahutuslikud probleemid." – M.: Teadus. Füüsikalise ja matemaatilise kirjanduse põhiväljaanne, 1985. - 160 lk.

Perelman Ya.I. Kiire konto. Kolmkümmend lihtsat vaimse loendamise meetodit. L., 1941 - 12 lk.

Perelman Ya.I. Meelelahutuslik aritmeetika. M.Rusanova, 1994–205lk.

Entsüklopeedia “Ma tunnen maailma. Matemaatika". – M.: Astrel Ermak, 2004.

Entsüklopeedia lastele. "Matemaatika". - M.: Avanta +, 2003. - 688 lk.

Saada oma head tööd teadmistebaasi on lihtne. Kasutage allolevat vormi

Üliõpilased, magistrandid, noored teadlased, kes kasutavad teadmistebaasi oma õpingutes ja töös, on teile väga tänulikud.

postitatud http://www.allbest.ru/

Originaalsed mitmekohaliste arvude korrutamise viisid ja nende rakendamise võimalus matemaatikatundides

Juhendaja:

Šaškova Jekaterina Olegovna

Sissejuhatus

1. Natuke ajalugu

2. Korrutamine sõrmedel

3. Korrutage 9-ga

4. India korrutamisviis

5. Korrutamine "Väikese lossi" meetodil

6. Korrutamine "armukadeduse" meetodil

7. Talupoja korrutamisviis

8. Uus viis paljundamiseks

Järeldus

Kirjandus

Sissejuhatus

Inimesel on igapäevaelus võimatu ilma arvutusteta hakkama saada. Seetõttu õpetatakse meid matemaatikatundides ennekõike arvudega tehteid sooritama ehk loendama. Korrutame, jagame, liidame ja lahutame kõigile koolis õpitavatele tavapärastel viisidel.

Kord sattusin kogemata ühe S.N. Olehnika, Yu.V. Nesterenko ja M.K. Potapov "Vanad meelelahutuslikud probleemid". Seda raamatut lehitsedes tõmbas mu tähelepanu lehekülg nimega "Korrutamine sõrmedel". Selgus, et korrutada saab mitte ainult nii, nagu nad meile matemaatikaõpikutes pakuvad. Mõtlesin, kas on veel mingeid arvutamise viise. Lõppude lõpuks on kiire arvutuste tegemise võimalus ausalt öeldes üllatav.

Kaasaegse arvutustehnoloogia pidev kasutamine toob kaasa asjaolu, et õpilastel on raske teha mingeid arvutusi, kui neil pole käsutuses tabeleid või arvutusmasinat. Lihtsustatud arvutustehnikate tundmine võimaldab mitte ainult peas kiiresti teha lihtsaid arvutusi, vaid ka mehhaniseeritud arvutuste tulemusena kontrollida, hinnata, leida ja parandada vigu. Lisaks arendab arvutusoskuste arendamine mälu, tõstab matemaatilise mõtlemiskultuuri taset, aitab täielikult assimileerida füüsilise ja matemaatilise tsükli aineid.

Eesmärk:

Näita ebatavalist korrutamismeetodid.

Ülesanded:

W Otsige üles nii palju kui võimalik ebatavalised arvutusviisid.

Ø Õppige neid kasutama.

Ш Valige enda jaoks koolis pakutavatest huvitavamad või lihtsamad ning kasutage neid loendamisel.

1. Natuke ajalugu

Praegu kasutatavad arvutusmeetodid ei olnud alati nii lihtsad ja mugavad. Vanasti kasutati tülikamaid ja aeglasemaid meetodeid. Ja kui 21. sajandi koolipoiss saaks reisida viis sajandit tagasi, avaldaks ta meie esivanematele muljet oma arvutuste kiiruse ja täpsusega. Kuulujutt temast oleks levinud ümberkaudsetes koolides ja kloostrites, varjutades tolle ajastu osavamate lettide hiilguse ja uue suure meistri juurde oleks tulnud kõikjalt õppima.

Eriti rasked olid vanasti korrutamise ja jagamise toimingud. Sel ajal ei olnud iga tegevuse jaoks välja töötatud ühte tehnikat. Vastupidi, korraga oli kasutusel ligi kümmekond erinevat korrutamis- ja jagamismeetodit – üks keerulisem kui teine, mida keskmise võimekusega inimene ei mäletanudki. Iga arvutamise õpetaja hoidis kinni oma lemmikmeetodist, iga "jagamismeister" (oli selliseid spetsialiste) kiitis oma viisi selle toimingu sooritamiseks.

V. Bellyustini raamatus “Kuidas inimesed järk-järgult jõudsid tõelise aritmeetikani” on välja toodud 27 korrutamismeetodit ja autor märgib: “On täiesti võimalik, et raamatuhoidlate süvendites on peidus rohkem meetodeid, mis on hajutatud paljudes , peamiselt käsitsi kirjutatud kogud.

Ja kõik need korrutamistehnikad - "male või orel", "painutamine", "rist", "võre", "tagasi ette", "teemant" ja teised võistlesid omavahel ja assimileeriti suurte raskustega.

Vaatame kõige huvitavamaid ja lihtsamaid korrutamisviise.

2. Korrutamine sõrmedel

Vana-Vene meetod sõrmedel korrutamiseks on üks levinumaid meetodeid, mida vene kaupmehed on edukalt kasutanud juba mitu sajandit. Õpiti sõrmedel korrutama ühekohalisi numbreid 6-st 9-ni. Samas piisas ka näpulugemise algoskustest “ühes”, “paaris”, “kolmiks”, “neljas”, “ viiesed” ja “kümned”. Sõrmed toimisid siin abistava arvutusseadmena.

Selleks sirutasid nad ühelt poolt nii palju sõrmi, kuivõrd esimene tegur ületab arvu 5, ja teiselt poolt tegid nad sama teise teguri puhul. Ülejäänud sõrmed olid kõverdatud. Seejärel võeti väljasirutatud sõrmede arv (kokku) ja korrutati 10-ga, seejärel korrutati numbrid, mis näitavad, mitu sõrme oli kätel kõverdatud, ja liideti tulemused.

Näiteks korrutame 7 8-ga. Vaadeldavas näites painutatakse 2 ja 3 sõrme. Kui liita kokku painutatud sõrmede arv (2+3=5) ja korrutada painutamata sõrmede arv (2*3=6), siis saame soovitud korrutise kümnendite ja ühikute arvud vastavalt 56 . Nii saate arvutada kõigi ühekohaliste arvude korrutise, mis on suuremad kui 5.

3. Korrutage 9-ga

Arvu 9 korrutamine- 9 1, 9 2 ... 9 10 - on lihtsam mälust kustutada ja keerulisem käsitsi ümber arvutada liitmise teel, kuid just numbri 9 puhul on korrutamine hõlpsasti reprodutseeritav "sõrmedel". Siruta sõrmed mõlemale käele laiali ja keera peopesad endast eemale. Määrake vaimselt sõrmedele numbrid vahemikus 1 kuni 10, alustades vasaku käe väikesest sõrmest ja lõpetades parema käe väikese sõrmega (see on näidatud joonisel).

Oletame, et tahame 9 korrutada 6-ga. Painutame sõrme, mille arv on võrdne arvuga, millega üheksa korrutame. Meie näites peate painutama sõrme numbriga 6. Painutatud sõrmest vasakul olevate sõrmede arv näitab meile vastuses kümnete arvu, paremal olevate sõrmede arvu - ühtede arvu. Vasakul on 5 sõrme painutamata, paremal - 4 sõrme. Seega 9 6=54. Allolev joonis näitab üksikasjalikult kogu "arvutamise" põhimõtet.

Teine näide: peate arvutama 9 8=?. Tee peal ütleme, et sõrmed ei pruugi tingimata toimida "arvutusmasinana". Võtke näiteks märkmikus 10 lahtrit. Tõmbame 8. lahtri maha. Vasakul on 7 lahtrit, paremal 2 lahtrit. Seega 9 8=72. Kõik on väga lihtne. korrutamise meetod lihtsustatud huvitav

4. India korrutamisviis

Kõige väärtuslikum panus matemaatiliste teadmiste varakambrisse anti Indias. Hindud pakkusid välja viisi, kuidas me kasutame arvude kirjutamiseks kümmet märki: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Selle meetodi aluseks on idee, et sama number tähistab ühikuid, kümneid, sadu või tuhandeid, olenevalt sellest, kus see arv asub. Numbrite puudumisel määratakse hõivatud koht numbritele määratud nullidega.

Indiaanlased arvasid hästi. Nad mõtlesid välja väga lihtsa viisi korrutamiseks. Nad sooritasid korrutamise, alustades kõrgeimast järjekorrast, ja kirjutasid mittetäielikud korrutised üles korrutise kohale, osade kaupa. Samas oli kohe näha ka terviktoote vanem number ja lisaks oli välistatud ühegi numbri ärajätmine. Korrutamismärki polnud veel teada, mistõttu jätsid nad tegurite vahele väikese vahemaa. Näiteks korrutame need viisil 537 6-ga:

5. Korrutatudpole võimalik"VÄIKE LOSSI"

Nüüd õpitakse kooli esimeses klassis arvude korrutamist. Kuid keskajal valdasid korrutamise kunsti väga vähesed. Haruldane aristokraat võis kiidelda korrutustabeli tundmisega, isegi kui ta on lõpetanud mõne Euroopa ülikooli.

Matemaatika arengu aastatuhandete jooksul on leiutatud palju võimalusi arvude korrutamiseks. Itaalia matemaatik Luca Pacioli loetleb oma traktaadis The Sum of Knowledge in Aritmetic, Relations and Proportionality (1494) kaheksa erinevat korrutamismeetodit. Esimene neist kannab nime "Väike loss", teine ​​aga mitte vähem romantiline nimega "Armukadedus või võrekorrutis".

“Väikese lossi” korrutamismeetodi eeliseks on see, et kõige kõrgemate numbrite numbrid määratakse algusest peale ja see võib olla oluline, kui on vaja väärtust kiiresti hinnata.

Ülemise arvu numbrid, alustades kõige olulisemast numbrist, korrutatakse vaheldumisi alumise numbriga ja kirjutatakse veergu, lisades vajaliku arvu nulle. Seejärel liidetakse tulemused kokku.

6. Nutikasnumbridmeetod"Armukadedus»

Teist meetodit nimetatakse romantiliselt "armukadeduseks" või "võrekorrutamiseks".

Kõigepealt joonistatakse ristkülik, mis on jagatud ruutudeks ja ristküliku külgede mõõtmed vastavad kordaja ja kordaja kümnendkohtade arvule. Seejärel jagatakse ruudukujulised lahtrid diagonaalselt ja "... selgub pilt, mis näeb välja nagu võre aknaluugid, rulood," kirjutab Pacioli. "Sellised aknaluugid riputati Veneetsia majade akendele, mis takistasid möödujatel akendel istuvaid daame ja nunnasid näha."

Korrutame sel viisil 347 29. Joonistame tabeli, kirjutame selle kohale arv 347 ja paremale arv 29.

Igal real kirjutame selle lahtri kohale ja sellest paremale arvude korrutise, kaldkriipsu kohale aga korrutise kümnendite arv ja selle alla ühikute arv. Nüüd liidage iga kaldkriipsu numbrid, tehes seda toimingut paremalt vasakule. Kui summa on väiksem kui 10, siis kirjutame selle riba alumise numbri alla. Kui selgub, et see on suurem kui 10, siis kirjutame ainult summa ühikute arvu ja lisame kümnete arvu järgmisele summale. Selle tulemusena saame soovitud toote 10063.

7 . Tomaalähedane korrutamisviis

Minu arvates on kõige "omamaisem" ja lihtsam korrutamisviis vene talupoegade kasutatav meetod. See meetod ei nõua üldjuhul teadmisi korrutustabeli kohta, mis on suurem kui arv 2. Selle olemus seisneb selles, et mis tahes kahe arvu korrutamine taandatakse ühe arvu järjestikusteks jagamisteks pooleks, samal ajal kui teise arvu kahekordistatakse. Poolitamine jätkub, kuni jagatis on 1, samal ajal kahekordistades paralleelselt teist arvu. Viimane kahekordistatud number annab soovitud tulemuse.

Paaritu arvu korral tuleb ühik ära visata ja ülejäänud osa pooleks jagada; kuid teisest küljest tuleb parempoolse veeru viimasele numbrile lisada kõik selle veeru numbrid, mis on vasakpoolse veeru paaritute numbrite vastu: summa on soovitud korrutis

Kõigi vastavate arvupaaride korrutis on sama, seega

37 32 = 1184 1 = 1184

Kui üks numbritest on paaritu või mõlemad numbrid on paaritud, toimige järgmiselt.

24 17 = 24 (16+1)=24 16 + 24 = 384 + 24 = 408

8 . Uus viis paljundamiseks

Hiljuti on teatatud uuest huvitavast korrutamisviisist. Uue mentaalse loendamise süsteemi leiutaja, filosoofiadoktor Vassili Okonešnikov väidab, et inimene on võimeline pähe õppima tohutul hulgal infot, peaasi, kuidas seda infot järjestada. Teadlase enda sõnul on üheksa kümnendkoha süsteem selles osas kõige soodsam – kõik andmed on lihtsalt paigutatud üheksasse lahtrisse, mis on paigutatud kalkulaatori nuppudena.

Sellise tabeli järgi on väga lihtne kokku lugeda. Näiteks korrutame arvu 15647 5-ga. Tabeli viiele vastavas osas valime järjekorras numbri numbritele vastavad arvud: üks, viis, kuus, neli ja seitse. Saame: 05 25 30 20 35

Vasak number (meie näites null) jäetakse muutmata ja paarikaupa lisatakse järgmised numbrid: viis kahega, viis kolmega, null kahega, null kolmega. Ka viimane number on muutumatu.

Selle tulemusena saame: 078235. Arv 78235 on korrutamise tulemus.

Kui kahe numbri liitmisel saadakse arv, mis ületab üheksat, lisatakse selle esimene number tulemuse eelmisele numbrile ja teine ​​kirjutatakse selle asemele.

Kõigist leitud ebatavalistest loendusmeetoditest tundus kõige huvitavam meetod „võrekorrutamine või armukadedus”. Näitasin seda oma klassikaaslastele ja ka neile meeldis see väga.

Lihtsaim meetod tundus mulle vene talupoegade poolt kasutatav kahekordistamise ja poolitamise meetod. Kasutan seda mitte liiga suurte arvude korrutamisel (kahekohaliste arvude korrutamisel on väga mugav kasutada).

Mind huvitas uus korrutamisviis, sest see võimaldab mõtetes tohutuid numbreid "keerata".

Ma arvan, et ka meie veeruga korrutamise meetod ei ole täiuslik ning me saame välja mõelda veelgi kiiremaid ja usaldusväärsemaid meetodeid.

Kirjandus

1. Depman I. "Lugusid matemaatikast". - Leningrad.: Haridus, 1954. - 140 lk.

2. Kornejev A.A. Vene korrutamise fenomen. Lugu. http://numbernautics.ru/

3. OlehnikS. N., Nesterenko Yu. V., Potapov M. K. "Vanad meelelahutuslikud probleemid." - M.: Teadus. Füüsikalise ja matemaatilise kirjanduse põhiväljaanne, 1985. - 160 lk.

4. Perelman Ya.I. Kiire konto. Kolmkümmend lihtsat vaimse loendamise meetodit. L., 1941 - 12 lk.

5. Perelman Ya.I. Meelelahutuslik aritmeetika. M.Rusanova, 1994--205lk.

6. Entsüklopeedia “Ma tunnen maailma. Matemaatika". - M.: Astrel Ermak, 2004.

7. Entsüklopeedia lastele. "Matemaatika". - M.: Avanta +, 2003. - 688 lk.

Majutatud saidil Allbest.ru

...

Sarnased dokumendid

Kuidas inimesed loendama õppisid, numbrite, numbrite ja numbrisüsteemide tekkimine. Korrutustabel "sõrmedel": arvude 9 ja 8 korrutamistehnika. Kiirloendamise näited. Kahekohalise arvu korrutamise viisid arvuga 11, 111, 1111 jne. ja kolmekohaline arv 999 võrra.

kursusetöö, lisatud 22.10.2011


Eratosthenese sõela meetodi rakendamine otsimiseks etteantud algarvude jadast kuni mõne täisarvuni. Kaksikute algarvude probleemi käsitlemine. Kahe algarvu lõpmatuse tõestus esimese astme algpolünoomis.

test, lisatud 05.10.2010


Sissejuhatus korrutamisse ja jagamisse. Summa tootega asendamise juhtumite arvestamine. Näidete lahendused samade ja erinevate terminitega. Jagamise arvutusmeetod, jagamine võrdseteks osadeks. Korrutustabelite õpetamine mängulises vormis.

esitlus, lisatud 15.04.2015


Algarvude tähenduse uurimise ajaloo iseloomustus matemaatikas, kirjeldades, kuidas need leitakse. Pietro Cataldi panus algarvude teooria arendamisse. Eratosthenese meetod algarvude tabelite koostamiseks. Naturaalarvude sõbralikkus.

test, lisatud 24.12.2010


Aritmeetika-loogiliste ühikute otstarve, koostis ja struktuur, liigitus, esitusvahendid. ALU arvutite ehituse ja toimimise põhimõtted. Korrutamisalgoritmi plokkskeemi koostamine, juhtsignaalide hulga määramine, vooluringi projekteerimine.

kursusetöö, lisatud 25.10.2014


"Maatriksi" mõiste matemaatikas. Mis tahes suurusega maatriksi korrutamine (jagamine) suvalise arvuga. Kahe maatriksi korrutamise tehted ja omadused. Transponeeritud maatriks on maatriks, mis saadakse algsest maatriksist, mille read on asendatud veergudega.

test, lisatud 21.07.2010


Algarvude uurimise ajaloolised faktid antiikajal, probleemi praegune seis. Algarvude jaotus arvude loomulikus reas, nende käitumise olemus ja põhjus. Kaksikute algarvude jaotuse analüüs tagasisideseaduse alusel.

artikkel, lisatud 28.03.2012


Kuupvõrrandite põhimõisted ja definitsioonid, nende lahendamise viisid. Cardano valem ja Vieta trigonomeetriline valem, loendusmeetodi olemus. Kuubikute erinevuse lühendatud korrutamise valemi rakendamine. Ruuttrinoomi juure definitsioon.

kursusetöö, lisatud 21.10.2013


Erinevate kombinatoorsete probleemide näidete käsitlemine matemaatikas. Võimalike valikute loetlemise viiside kirjeldus. Kombinatoorse korrutamisreegli kasutamine. Valikute puu ehitamine. Permutatsioonid, kombinatsioonid, paigutused kui kõige lihtsamad kombinatsioonid.

esitlus, lisatud 17.10.2015


Maatriksi omavektori määramine maatriksi poolt antud lineaarse teisenduse rakendamise tulemusena (vektori korrutamine omaväärtusega). Peamiste toimingute loetelu ja Leverrier-Faddejevi meetodi algoritmi plokkskeemi kirjeldus.

Neli tuhat aastat tagasi leiutasid babüloonlased korrutamise. Ja selle aasta märtsis parandasid matemaatikud seda.

18. märtsil 2019 kirjeldasid kaks teadlast kiireimat teadaolevat meetodit kahe väga suure arvu korrutamiseks. Teos tähistab pikaajaliste otsingute kulminatsiooni matemaatika ühe põhitehte täitmiseks kõige tõhusama protseduuri järele.

"Kõik arvavad, et koolis õpitud korrutamismeetod on parim, kuid tegelikult on selles valdkonnas käimas palju uuringuid," ütleb Prantsuse riikliku teadusuuringute keskuse matemaatik Joris van der Hoeven ja üks koostööpartneritest. - töö autorid.

Paljude arvutusprobleemide keerukus alates π uute numbrite loendamisest kuni suurte algarvude leidmiseni taandub korrutamise kiirusele. Van der Hoeven kirjeldab nende tulemust kui matemaatilise kiiruspiirangu määramist paljudele teistele probleemidele.

"Füüsikas on olulised konstandid, nagu valguse kiirus, mis võimaldavad teil asju kirjeldada, " ütles van der Hoeven. "Kui soovite teada, kui kiiresti suudavad arvutid teatud matemaatilisi probleeme lahendada, siis täisarvude korrutamine on omamoodi põhiline ehitusplokk, millega saate sellist kiirust väljendada."

Peaaegu kõik õpivad numbreid korrutama ühtemoodi. Kirjutame numbrid veergu, korrutame ülemise numbri iga alumise numbriga (arvestades numbreid) ja lisame tulemuse. Kahe kahekohalise arvu korrutamisel tuleb lõpptulemuse saamiseks teha neli väiksemat korrutamist.

Kooli meetod "ülekandmine" nõuab n 2 sammu, kus n on numbrite arv igas korrutatud arvus. Kolmekohaliste arvudega arvutamiseks on vaja üheksa korrutamist ja sajakohaliste arvudega - 10 000.

Kandmismeetod töötab hästi mõnekohaliste numbritega, kuid see takerdub miljonite või miljardite numbritega arvude korrutamisel (mida arvutid teevad, kui loendavad pii-d täpselt või otsivad maailmas suuri algarvusid). Kahe miljardi numbriga arvu korrutamiseks oleks vaja miljard ruudus ehk 10 18 korrutamist, mis võtaks kaasaegsel arvutil aega umbes 30 aastat.

Mitu aastatuhandet usuti, et numbreid on võimatu kiiremini korrutada. Seejärel, 1960. aastal, osales 23-aastane Nõukogude ja Vene matemaatik Anatoli Aleksejevitš Karatsuba seminaril, mida juhtis nõukogude matemaatik, 20. sajandi üks suurimaid matemaatikuid Andrei Nikolajevitš Kolmogorov. Kolmogorov väitis, et ei ole olemas üldistatud korrutamisviisi, mis nõuaks vähem kui n 2 tehteid. Karatsuba otsustas, et selline viis on olemas – ja pärast nädalast otsimist ta selle avastas.

Anatoli Aleksejevitš Karatsuba

Karatsuba korrutamine seisneb arvu numbrite tükeldamises ja nende uuesti kombineerimises uuel viisil, mis võimaldab suur hulk korrutamine teostab vähem liitmisi ja lahutamisi. Meetod säästab aega, sest liitmine võtab n 2 asemel vaid 2n sammu.

Traditsiooniline 25x63 korrutamismeetod nõuab nelja ühekohalist korrutamist ja paari liitmist.

25x63 Karatsuba korrutamine nõuab kolme ühekohalist korrutamist ning mõnda liitmist ja lahutamist.
a) numbrite poolitamine
b) korrutada kümnetega
c) korrutage ühikuid
d) liida numbrid kokku
e) korrutage need summad
f) e – b – c loendamine
g) koguda lõppsumma punktidest b, c ja f

Märkide arvu suurenemisega numbrites saab Karatsuba meetodit kasutada rekursiivselt.

Traditsiooniline 2531x1467 korrutamismeetod nõuab 16 ühekohalist korrutamist.

Karatsuba 2531x1467 korrutamiseks on vaja 9 korrutamist.

"Lisamine toimub koolis aasta varem, sest see on palju lihtsam, seda tehakse lineaarselt, numbrite vasakult paremale lugemise kiirusega," ütles Pennsylvania matemaatik Martin Führer. riigiülikool, kes lõi 2007. aastal tolle aja kiireima korrutamisalgoritmi.

Suurte arvude käsitlemisel saab Karatsuba korrutamist korrata rekursiivselt, jagades algsed arvud peaaegu nii paljudeks osadeks, kui palju on neis märke. Ja iga jagamisega muudate korrutamist, mis nõuab palju samme, liitmiseks ja lahutamiseks, mis nõuab palju vähem samme.

"Mõned korrutused saab muuta liitmisteks, kuna arvutid saavad seda kiiremini teha," ütles David Harvey, New South Walesi ülikooli matemaatik ja uue töö kaasautor.

Karatsuba meetod võimaldas arve korrutada, kasutades ainult n 1,58 ühekohalist korrutamist. Seejärel avaldasid Arnold Schönhage ja Volker Strassen 1971. aastal meetodi suurte arvude korrutamiseks n × log n × log (log n) väikeste korrutustega. Kahe miljardikohalise arvu korrutamiseks vajaks Karatsuba meetod 165 triljonit sammu.

Joris van der Hoeven, Prantsuse riikliku teadusuuringute keskuse matemaatik

Schönhage-Strasseni meetodit kasutavad arvutid suurte arvude korrutamiseks ja see on toonud kaasa veel kaks olulist tagajärge. Esiteks tutvustas ta signaalitöötlustehnikat, mida nimetatakse kiireks Fourier' teisenduseks. Sellest ajast peale on see tehnika olnud kõigi kiirete korrutamisalgoritmide aluseks.

Teiseks soovitasid Schönhage ja Strassen samas artiklis veelgi kiirema algoritmi võimalust – meetodit, mis nõuab ainult n × log n korrutamist sama märgiga – ja et selline algoritm oleks võimalikult kiire. See eeldus põhines tundel, et sellise põhitehte nagu korrutamine puhul tuleks tehtete piirang kirjutada kuidagi elegantsemalt kui n × log n × log (log n).

"Enamasti nõustutakse, et korrutamine on nii oluline põhioperatsioon, et puhtalt esteetilisest vaatenurgast vajab see keerukuse piiranguid," ütles Fuhrer. "Kogemusest teame, et põhitõdede taga olev matemaatika on alati elegantne."

Ebamugav Schönhage'i ja Strasseni piirang, n × log n × log (log n), kehtis 36 aastat. 2007. aastal purustas Fuhrer selle rekordi ja kõik hakkas keerlema. Viimase kümnendi jooksul on matemaatikud leidnud üha kiiremaid korrutamisalgoritme, millest igaüks on järk-järgult hiilinud n × log n märgini, mitte päris selleni jõudnud. Siis selle aasta märtsis jõudsid Harvey ja van der Hoeven selleni.

Nende meetod on suure hulga enne neid tehtud töö täiustamine. See jagab numbrid märkideks, kasutab kiire Fourier' teisenduse täiustatud versiooni ja kasutab ära muid viimase 40 aasta jooksul tehtud läbimurdeid. "Me kasutame FFT-d palju toorasemalt, kasutades seda mitu korda, mitte ainult üks kord, ja asendame veelgi rohkem korrutamisi liitmise ja lahutamisega," ütles van der Hoeven.

Harvey ja van der Hoeveni algoritm tõestab, et korrutamist saab teha n × log n sammuga. See aga ei tõenda kiirema meetodi puudumist. Palju keerulisem on kindlaks teha, et nende lähenemine on võimalikult kiire. Veebruari lõpus avaldas Århusi ülikooli arvutiteadlaste meeskond töö, milles väideti, et kui üks tõestamata teoreemidest osutub tõeks, on see meetod tõepoolest kiireim viis korrutamiseks.

Ja kuigi see uus algoritm on teoreetiliselt väga oluline, ei muutu see praktikas palju, kuna see ületab juba kasutatavaid algoritme vaid veidi. "Me võime loota vaid kolmekordset kiirust," ütles van der Hoeven. "Mitte midagi ennekuulmatut."

Lisaks on muutunud arvutiseadmete skeemid. Kakskümmend aastat tagasi tegid arvutid liitmise palju kiiremini kui korrutamist. Kiirusevahe korrutamise ja liitmise vahel on sellest ajast alates märkimisväärselt vähenenud, mistõttu võib korrutamine mõnel kiibil isegi liitmisest mööduda. Teatud tüüpi riistvaraga "saate liitmist kiirendada, kui arvuti korrutab numbreid ja see on omamoodi hull, " ütles Harvey.

Riistvara muutub aja jooksul, kuid oma klassi parimad algoritmid kestavad igavesti. Olenemata sellest, millised arvutid tulevikus välja näevad, on Harvey ja van der Hoeveni algoritm endiselt kõige olulisem tõhus viis arvude korrutamine.

Mõned kiired viisid verbaalne korrutamine oleme selle teiega juba lahendanud, nüüd vaatame lähemalt, kuidas erinevate abimeetodite abil kiiresti arve oma mõtetes korrutada. Võib-olla teate juba ja mõned neist on üsna eksootilised, näiteks iidne Hiina viis arvude korrutamiseks.

Järjestus kategooriate järgi

See on lihtsaim viis kahekohaliste arvude kiireks korrutamiseks. Mõlemad tegurid tuleb jagada kümneteks ja ühtedeks ning seejärel kõik need uued arvud omavahel korrutada.

See meetod eeldab võimalust hoida mälus korraga kuni nelja numbrit ja teha nende arvudega arvutusi.

Näiteks peate arvud korrutama 38 ja 56 . Teeme seda nii:

38 * 56 = (30 + 8) * (50 + 6) = 30 * 50 + 8 * 50 + 30 * 6 + 8 * 6 = 1500 + 400 + 180 + 48 = 2128 Kahekohaliste arvude peast korrutamist kolmes etapis on veelgi lihtsam teha. Kõigepealt peate korrutama kümned, seejärel liitma kaks korrutist ühega kümnetega ja seejärel liitma ühe korrutise ühega. See näeb välja selline: 38 * 56 = (30 + 8) * (50 + 6) = 30 * 50 + (8 * 50 + 30 * 6) + 8 * 6 = 1500 + 580 + 48 = 2128 Selle meetodi edukaks kasutamiseks on vaja hästi tunda korrutustabelit, osata kiiresti liita kahe- ja kolmekohalisi arve ning vahetada matemaatilisi tehteid, unustamata ka vahetulemusi. Viimane oskus saavutatakse abi ja visualiseerimisega.

See meetod ei ole kõige kiirem ja tõhusam, seega tasub uurida teisi verbaalse korrutamise viise.

Numbri sobitamine

Võite proovida viia aritmeetilise arvutuse mugavamale kujule. Näiteks arvude korrutis 35 ja 49 võib ette kujutada nii: 35 * 49 = (35 * 100) / 2 — 35 = 1715
See meetod võib olla eelmisest tõhusam, kuid see ei ole universaalne ega sobi kõikidel juhtudel. Ülesande lihtsustamiseks ei ole alati võimalik sobivat algoritmi leida.

Sel teemal meenutasin anekdooti, ​​kuidas matemaatik mööda jõge ühest talust mööda purjetas ja rääkis vestluskaaslastele, et tal õnnestus kiiresti kokku lugeda aedikus olevate lammaste arv, 1358 lammast. Küsimusele, kuidas ta seda tegi, vastas ta, et kõik on lihtne - peate loendama jalgade arvu ja jagama 4-ga.

Korrutamise visualiseerimine veerus

See on üks mitmekülgsemaid arvude mõttelise korrutamise viise, mis arendab ruumilist kujutlusvõimet ja mälu. Kõigepealt peate õppima, kuidas kahekohalisi arve oma mõtetes veerus ühekohaliste arvudega korrutada. Pärast seda saate kahekohalisi arve hõlpsalt kolme sammuga korrutada. Esiteks tuleb kahekohaline arv korrutada mõne teise arvu kümnetega, seejärel korrutada teise arvu ühikutega ja seejärel saadud arvud kokku liita.

See näeb välja selline: 38 * 56 = (38 * 5) * 10 + 38 * 6 = 1900 + 228 = 2128

Visualiseerimine numbrite paigutusega

Väga huvitav viis kahekohaliste arvude korrutamiseks on järgmine. Sadade, ühtede ja kümnete saamiseks on vaja arvud arvudega korrutada.

Oletame, et soovite korrutada 35 peal 49 .

Kõigepealt korrutage 3 peal 4 , sa saad 12 , siis 5 ja 9 , sa saad 45 . Kirjuta üles 12 ja 5 , mille vahel on tühik ja 4 mäleta.

Sa saad: 12 __ 5 (pidage meeles 4 ).

Nüüd korrutage 3 peal 9 ja 5 peal 4 ja kokkuvõtteks: 3 * 9 + 5 * 4 = 27 + 20 = 47 .

Nüüd sa pead 47 lisama 4 mida me mäletame. Saame 51 .

Me kirjutame 1 keskel ja 5 Lisa 12 , saame 17 .

Niisiis, number, mida otsisime 1715 , see on vastus:

35 * 49 = 1715
Proovige vaimselt korrutada samal viisil: 18 * 34, 45 * 91, 31 * 52 .

Hiina või Jaapani korrutamine

Aasia riikides on kombeks arve korrutada mitte veerus, vaid joonte tõmbamisega. Ida kultuuride jaoks on oluline soov mõtiskleda ja visualiseerida, ilmselt seetõttu tulid nad välja nii ilusa meetodi, mis võimaldab korrutada mis tahes numbreid. See meetod on keeruline ainult esmapilgul. Tegelikult võimaldab suurem nähtavus seda meetodit palju tõhusamalt kasutada kui veerus korrutamist.

Lisaks suurendab selle iidse idamaise meetodi tundmine teie eruditsiooni. Nõus, mitte igaüks ei saa kiidelda iidse korrutussüsteemi tundmisega, mida hiinlased kasutasid 3000 aastat tagasi.

Video sellest, kuidas hiinlased numbreid korrutavad

Täpsemat teavet leiate jaotistest "Kõik kursused" ja "Kasulikkus", millele pääseb juurde saidi ülamenüü kaudu. Nendes jaotistes on artiklid rühmitatud teemade kaupa plokkidesse, mis sisaldavad kõige üksikasjalikumat (võimaluse piires) teavet erinevatel teemadel.

Samuti saate tellida ajaveebi ja tutvuda kõigi uute artiklitega.
See ei võta palju aega. Klõpsake lihtsalt alloleval lingil:

Pedagoogikateaduste kandidaat Natalia Karpushina.

Mitmekohaliste arvude korrutamise valdamiseks peate lihtsalt teadma korrutustabelit ja oskama numbreid liita. Sisuliselt seisneb kogu raskus selles, kuidas korrutamise vahetulemusi (osakorrutisi) õigesti paigutada. Püüdes arvutusi lihtsamaks muuta, on inimesed arvude korrutamiseks välja mõelnud mitmeid viise. Sajanditepikkuse matemaatika ajaloo jooksul on neid olnud mitukümmend.

Korrutamine võremeetodiga. Illustratsioon esimesest trükitud aritmeetikaraamatust. 1487.

Napier pulgad. Seda lihtsat loendusseadet kirjeldati esmakordselt John Napieri teoses "Rabdology". 1617.

John Napier (1550-1617).

Schikardi arvutusmasina mudel. Selle arvutusseadme, mis meieni pole jõudnud, valmistas leiutaja 1623. aastal ja kirjeldas seda aasta hiljem kirjas Johannes Keplerile.

Wilhelm Schickard (1592-1635).

Hindu pärand – riivimisviis

Hindud, kes tundsid kümnendarvude süsteemi iidsetest aegadest, eelistasid suulist arvestust kirjalikule. Nad leiutasid mitmeid viise kiireks paljunemiseks. Hiljem laenasid need araablased ja neilt läksid need meetodid üle eurooplastele. Need aga ei piirdunud nendega ja töötasid välja uued, eriti selle, mida koolis õpitakse - veeruga korrutamist. See meetod on tuntud 15. sajandi algusest, järgmisel sajandil kinnistus see matemaatikute seas kindlalt ja tänapäeval kasutatakse seda kõikjal. Kuid kas veeruga korrutamine on parim viis selle aritmeetilise tehte tegemiseks? Tegelikult on meie ajal ka teisi, unustatud korrutamismeetodeid, mitte halvem, näiteks võremeetod.

Seda meetodit kasutati antiikajal, keskajal oli see laialt levinud idas ja renessansiajal Euroopas. Võremeetodit nimetati ka india, moslemi või "rakus paljunemiseks". Ja Itaalias nimetati seda "gelosia" või "võre korrutis" (gelosia itaalia keelest tõlgituna - "rulood", "võrestiku luugid"). Tõepoolest, arvude korrutamisel saadud arvud meenutasid aknaluuke-ruloosid, mis sulgesid päikese eest Veneetsia majade aknad.

Selgitame selle lihtsa korrutamismeetodi olemust näitega: arvutame korrutise 296 × 73. Alustuseks joonistame numbrite arvu järgi ruudukujuliste lahtritega tabeli, milles on kolm veergu ja kaks rida. kordajad. Jagage rakud diagonaalselt pooleks. Tabeli kohale kirjutame arvu 296 ja paremale poole vertikaalselt numbri 73. Korrutame esimese numbri iga numbri teise numbriga ja kirjutame korrutised vastavatesse lahtritesse, asetades diagonaali kohale kümned ja ühikud. selle all. Soovitud toote numbrid saadakse kaldribades olevate numbrite liitmisel. Sel juhul liigume päripäeva, alustades alumisest paremast lahtrist: 8, 2 + 1 + 7 jne. Tulemused kirjutame tabeli alla, samuti sellest vasakule. (Kui liitmisel saadakse kahekohaline summa, märgime ainult ühikud ja lisame järgmise riba numbrite summale kümned.) Vastus: 21 608. Seega 296 x 73 = 21 608.

Võre meetod ei ole kuidagi madalam kui veeru korrutamine. See on veelgi lihtsam ja usaldusväärsem, hoolimata asjaolust, et mõlemal juhul sooritatavate toimingute arv on sama. Esiteks peate töötama ainult ühe- ja kahekohaliste numbritega ning neid on lihtne meeles pidada. Teiseks pole vaja vahetulemusi pähe õppida ja jälgida nende üleskirjutamise järjekorda. Mälu tühjeneb ja tähelepanu säilib, seega väheneb vea tõenäosus. Lisaks võimaldab võremeetod kiiresti saada tulemuse. Olles selle omandanud, näete ise.

Miks annab võremeetod õige vastuse? Mis on selle "mehhanism"? Selgitame selle välja tabeli abil, mis on koostatud sarnaselt esimesega, ainult sel juhul esitatakse tegurid summadena 200 + 90 + 6 ja 70 + 3.

Nagu näete, on esimeses kaldus ribas ühikud, teises kümned, kolmandas sadu jne. Lisamisel annavad nad vastuses vastavalt ühikute arvu, kümneid, sadu jne. See on ilmne:

Teisisõnu, vastavalt aritmeetikaseadustele arvutatakse arvude 296 ja 73 korrutis järgmiselt:

296 x 73 = (200 + 90 + 6) x (70 + 3) = 14000 + 6300 + 420 + 600 + 270 + 18 = 10000 + (4000 + 6000) + (300 + 400 + 60) + (720) + 20 + 10) + 8 = 21 608.

Napieri pulgad

Võremeetodiga korrutamise aluseks on lihtne ja originaalne loendusseade - Napieri pulgad. Selle leiutaja John Napier, Šoti parun ja matemaatika armastaja, tegeles koos professionaalidega arvutusvahendite ja -meetodite täiustamisega. Teadusajaloos on ta tuntud eelkõige ühe logaritmide loojana.

Seade koosneb kümnest joonlauast, millele asetatakse korrutustabel. Igas diagonaaliga eraldatud lahtris kirjutatakse kahe ühekohalise arvu korrutis 1 kuni 9: kümnete arv on näidatud ülemises osas, ühtede arv alumises osas. Üks joonlaud (vasakul) on fikseeritud, ülejäänuid saab ühest kohast teise ümber paigutada, paigutades soovitud numbrikombinatsiooni. Napieri pulkade abil on lihtne mitmekohalisi arve korrutada, vähendades selle toimingu liitmiseks.

Näiteks arvude 296 ja 73 korrutise arvutamiseks peate 296 korrutama 3-ga ja 70-ga (kõigepealt 7-ga, seejärel 10-ga) ning liitma saadud arvud. Fikseeritud joonlaua külge kinnitame veel kolm - numbritega 2, 9 ja 6 üleval (need peaksid moodustama numbri 296). Nüüd vaatame kolmandat rida (reanumbrid on näidatud äärmisel joonlaual). Selles olevad numbrid moodustavad meile juba tuttava komplekti.

Neid liites, nagu võremeetodi puhul, saame 296 x 3 = 888. Samamoodi, arvestades seitsmendat rida, leiame, et 296 x 7 = 2072, siis 296 x 70 = 20 720. Seega,
296 x 73 = 20 720 + 888 = 21 608.

Napieri pulgakesi kasutati ka keerukamate operatsioonide tegemiseks – jagamiseks ja ruutjuure ekstraheerimiseks. Seda loendusseadet on korduvalt üritatud täiustada ja muuta töös mugavamaks ja tõhusamaks. Tõepoolest, paljudel juhtudel oli arvude korrutamiseks, näiteks korduvate numbritega, vaja mitut pulgakomplekti. Kuid selline probleem lahendati, asendades joonlauad pöörlevate silindritega ja nende pinnale kanti korrutustabel samal kujul, nagu Napier seda esitas. Ühe pulgakomplekti asemel saadi korraga üheksa.

Sellised nipid tõesti kiirendasid ja hõlbustasid arvutusi, kuid ei mõjutanud Napieri seadme peamist tööpõhimõtet. Nii sai võremeetod teise elu, mis kestis veel mitu sajandit.

Shikkard masin

Teadlased on pikka aega mõelnud, kuidas viia raske arvutustöö mehaanilistele seadmetele. Esimesed edukad sammud arvutusmasinate loomisel tehti alles 17. sajandil. Arvatakse, et saksa matemaatik ja astronoom Wilhelm Schickard tegi sarnase mehhanismi varem kui teised. Kuid iroonilisel kombel teadis sellest vaid kitsas ring inimesi ja sellist kasulikku leiutist ei teadnud maailm enam kui 300 aastat. Seetõttu ei mõjutanud see arvutusseadmete edasist arendamist. Schikardi masina kirjeldus ja eskiisid avastati alles pool sajandit tagasi Johannes Kepleri arhiivist ning veidi hiljem loodi säilinud dokumentide järgi ka selle töömudel.

Sisuliselt on Schickardi masin kuuekohaline mehaaniline kalkulaator, mis teostab arvude liitmist, lahutamist, korrutamist ja jagamist. Sellel on kolm osa: korrutusseade, liitmisseade ja mehhanism vahetulemuste salvestamiseks. Esimese aluseks olid, nagu võite arvata, silindriteks rullitud Napieri pulgad. Nad olid kinnitatud kuue külge vertikaalteljed ja keerati masina ülaosas asuvate spetsiaalsete käepidemete abil. Silindrite ees oli paneel üheksa rea ​​akendega, igas kuus, mida avati ja suleti küljeriividega, kui oli vaja näha vajalikke numbreid ja peita ülejäänu.

Shikkard loendusmasinat on väga lihtne kasutada. Et teada saada, mis on 296 x 73 korrutis, tuleb silindrid seada asendisse, kus akende ülemisse rida ilmub esimene kordaja: 000296. Korrutise 296 x 3 saame avades aknad. kolmas rida ja nähtud arvude summeerimine, nagu võremeetodil. Samamoodi saame seitsmenda rea ​​aknaid avades korrutise 296 x 7, millele paremale liidame 0. Jääb vaid liita liitjalt leitud numbrid.

Kunagi indiaanlaste leiutatud kiire ja töökindel meetod mitmekohaliste arvude korrutamiseks, mida on arvutustes kasutatud sajandeid, on nüüd paraku unustatud. Aga ta oleks võinud meid tänagi hädast välja aidata, kui mitte kõigile nii tuttav kalkulaator.