Kõige lihtsamad trigonomeetrilised võrrandid on võrrandid

Cos(x)=a, sin(x)=a, tg(x)=a, ctg(x)=a

Võrrand cos(x) = a

Selgitus ja põhjendus

1. Võrrandi cosx = a juured. Millal | a | > 1 võrrandil pole juuri, sest | cosx |< 1 для любого x (прямая y = а при а >1 või kell a< -1 не пересекает график функцииy = cosx).

Laske | a |< 1. Тогда прямая у = а пересекает график функции

y = cos x. Intervallil väheneb funktsioon y = cos x 1-lt -1-le. Kuid kahanev funktsioon võtab kõik oma väärtused ainult ühes definitsioonipiirkonna punktis, seetõttu on võrrandil cos x \u003d a sellel intervallil ainult üks juur, mis kaarekoosinuse definitsiooni järgi on: x 1 \u003d arccos a (ja selle juure jaoks cos x \u003d a).

Koosinus on paarisfunktsioon, seega intervallil [-p; 0] võrrand cos x = ja sellel on samuti ainult üks juur - x 1 vastandarv, see on

x 2 = -arccos a.

Seega intervallil [-n; n] (pikkus 2n) võrrand cos x = a | a |< 1 имеет только корни x = ±arccos а.

Funktsioon y = cos x on perioodiline perioodiga 2n, seega kõik muud juured erinevad 2np (n € Z) poolt leitud juurtest. Võrrandi cos x = a millal juurte jaoks saame järgmise valemi

x = ± arccos a + 2n, n £ Z.

1. Võrrandi cosx = a lahendamise erijuhud.

Kasulik on meeles pidada võrrandi cos x = a millal juurte eritähistust

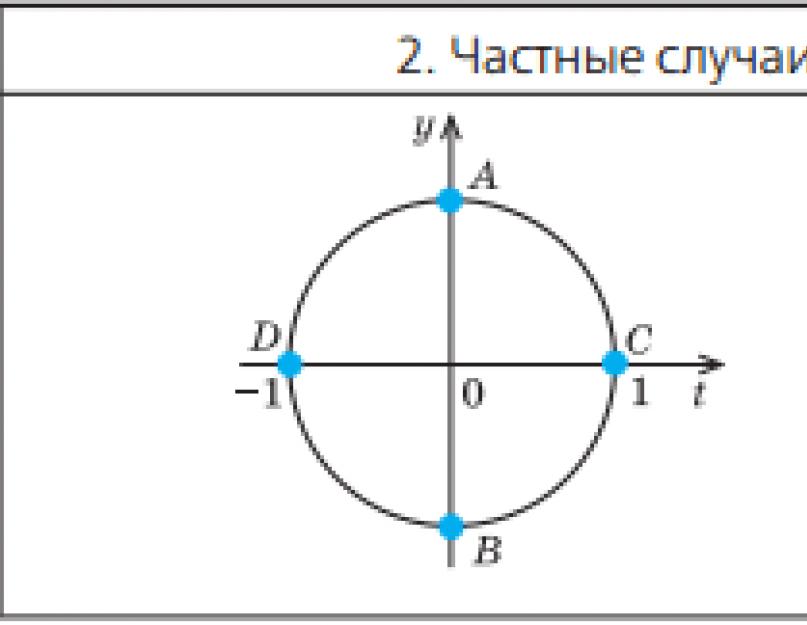
a \u003d 0, a \u003d -1, a \u003d 1, mille saab hõlpsasti kätte, kasutades juhendina ühikuringi.

Kuna koosinus on võrdne ühikringkonna vastava punkti abstsissiga, saame, et cos x = 0 siis ja ainult siis, kui ühikringi vastav punkt on punkt A või punkt B.

Samamoodi cos x = 1 siis ja ainult siis, kui ühikringi vastav punkt on punkt C, seega

x = 2πp, k € Z.

Samuti cos x \u003d -1 siis ja ainult siis, kui ühikringi vastav punkt on punkt D, seega x \u003d n + 2n,

Võrrand sin(x) = a

Selgitus ja põhjendus

1. Võrrandi sinx = a juured. Millal | a | > 1 võrrandil pole juuri, sest | sinx |< 1 для любого x (прямая y = а на рисунке при а >1 või kell a< -1 не пересекает график функции y = sinx).

Peamised trigonomeetriliste võrrandite lahendamise meetodid on: võrrandite taandamine kõige lihtsamateks (trigonomeetriliste valemite abil), uute muutujate sisseviimine, faktooring. Vaatleme nende rakendamist näidetega. Pöörake tähelepanu trigonomeetriliste võrrandite lahendi registreerimisele.

Trigonomeetriliste võrrandite eduka lahendamise vajalik tingimus on trigonomeetriliste valemite tundmine (6. töö 13. teema).

Näited.

1. Lihtsaima taandamise võrrandid.

1) Lahenda võrrand

Lahendus:

Vastus:

2) Leidke võrrandi juured

(sinx + cosx) 2 = 1 – segmenti kuuluv sinxcosx .

Lahendus:

Vastus:

2. Ruutvõrranditeks taandavad võrrandid.

1) Lahendage võrrand 2 sin 2 x - cosx -1 = 0.

Lahendus: Kasutades valemit sin 2 x \u003d 1 - cos 2 x, saame

Vastus:

2) Lahendage võrrand cos 2x = 1 + 4 cosx.

Lahendus: Kasutades valemit cos 2x = 2 cos 2 x - 1, saame

Vastus:

3) Lahendage võrrand tgx - 2ctgx + 1 = 0

Lahendus:

Vastus:

3. Homogeensed võrrandid

1) Lahendage võrrand 2sinx - 3cosx = 0

Lahendus: Olgu cosx = 0, siis 2sinx = 0 ja sinx = 0 – vastuolu sellega, et sin 2 x + cos 2 x = 1. Seega cosx ≠ 0 ja võrrandi saab jagada cosx-iga. Hangi

Vastus:

2) Lahendage võrrand 1 + 7 cos 2 x = 3 sin 2x

Lahendus:

Kasutades valemeid 1 = sin 2 x + cos 2 x ja sin 2x = 2 sinxcosx, saame

sin2x + cos2x + 7cos2x = 6sinxcosx
sin2x – 6sinxcosx+ 8cos2x = 0

Olgu cosx = 0, siis sin 2 x = 0 ja sinx = 0 - vastuolu tõsiasjaga, et sin 2 x + cos 2 x = 1.
Seega cosx ≠ 0 ja saame võrrandi jagada cos 2 x-ga . Hangi

tg 2x – 6 tgx + 8 = 0
Tähistage tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y2=2
a) tanx = 4, x = arctg4 + 2 k, k
b) tgx = 2, x = arctg2 + 2 k, k .

Vastus: arctg4 + 2 k, arctan2 + 2 k, k

4. Vormi võrrandid a sinx + b cosx = koos, koos≠ 0.

1) Lahenda võrrand.

Lahendus:

Vastus:

5. Faktoriseerimisega lahendatud võrrandid.

1) Lahendage võrrand sin2x - sinx = 0.

Võrrandi juur f (X) = φ ( X) saab olla ainult number 0. Kontrollime seda:

cos 0 = 0 + 1 - võrdus on tõene.

Arv 0 on selle võrrandi ainus juur.

Vastus: 0.

Saate tellida oma probleemile üksikasjaliku lahenduse !!!

Võrdsust, mis sisaldab tundmatut trigonomeetrilise funktsiooni märgi all (`sin x, cos x, tg x` või `ctg x`), nimetatakse trigonomeetriliseks võrrandiks ja me käsitleme nende valemeid edasi.

Lihtsamad võrrandid on "sin x=a, cos x=a, tg x=a, ctg x=a", kus "x" on leitav nurk, "a" on suvaline arv. Kirjutame igaühe jaoks juurvalemid.

1. Võrrand "sin x=a".

„|a|>1” puhul pole sellel lahendusi.

Koos `|a| \leq 1`-l on lõpmatu arv lahendusi.

Juurvalem: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Võrrand „cos x=a”.

`|a|>1` puhul - nagu siinuse puhul, pole reaalarvude hulgas lahendeid.

Koos `|a| \leq 1`-l on lõpmatu arv lahendusi.

Juurvalem: `x=\pm arccos a + 2\pi n, n \in Z`

Siinuse ja koosinuse erijuhud graafikutes.

3. Võrrand „tg x=a”.

Sellel on lõpmatu arv lahendusi mis tahes "a" väärtuste jaoks.

Juurvalem: `x=arctg a + \pi n, n \in Z`

4. Võrrand „ctg x=a”.

Sellel on ka lõpmatu arv lahendusi mis tahes "a" väärtuste jaoks.

Juurvalem: `x=arcctg a + \pi n, n \in Z`

Tabeli trigonomeetriliste võrrandite juurte valemid

Siinuse puhul:
Koosinuse jaoks:
Tangensi ja kotangensi jaoks:
Valemid pöördtrigonomeetrilisi funktsioone sisaldavate võrrandite lahendamiseks:

Trigonomeetriliste võrrandite lahendamise meetodid

Mis tahes trigonomeetrilise võrrandi lahendamine koosneb kahest etapist:

• kasutades selle teisendamiseks kõige lihtsamaks;
• lahendage saadud lihtne võrrand, kasutades ülaltoodud juurte ja tabelite valemeid.

Vaatleme näidete abil peamisi lahendusviise.

algebraline meetod.

Selle meetodi puhul toimub muutuja asendamine ja selle asendamine võrdsusega.

Näide. Lahendage võrrand: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0,

tehke asendus: "cos(x+\frac \pi 6)=y", siis "2y^2-3y+1=0",

leiame juured: `y_1=1, y_2=1/2`, millest järgneb kaks juhtumit:

1. „cos(x+\frac \pi 6)=1”, „x+\frac \pi 6=2\pi n”, „x_1=-\frac \pi 6+2\pi n”.

2. `cos(x+\frac \pi 6)=1/2, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Vastus: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Faktoriseerimine.

Näide. Lahendage võrrand: `sin x+cos x=1`.

Lahendus. Liigutage kõik võrdsuse tingimused vasakule: "sin x+cos x-1=0". Kasutades , teisendame ja faktoriseerime vasaku külje:

"sin x - 2sin^2 x/2=0",

"2sin x/2 cos x/2-2sin^2 x/2=0",

"2sin x/2 (cos x/2-sin x/2) = 0",

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. „cos x/2-sin x/2=0”, „tg x/2=1”, „x/2=arctg 1+ \pi n”, „x/2=\pi/4+ \pi n” , `x_2=\pi/2+ 2\pi n`.

Vastus: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Taandamine homogeenseks võrrandiks

Esiteks peate selle trigonomeetrilise võrrandi viima ühele kahest vormist:

`a sin x+b cos x=0` (esimese astme homogeenne võrrand) või `a sin^2 x + b sin x cos x +c cos^2 x=0` (teise astme homogeenne võrrand).

Seejärel jagage mõlemad osad esimesel juhul ühikuga "cos x \ne 0" ja teise puhul "cos^2 x \ne 0". `tg x` jaoks saame võrrandid: `a tg x+b=0` ja `a tg^2 x + b tg x +c =0`, mis tuleb lahendada tuntud meetoditega.

Näide. Lahendage võrrand: `2 sin^2 x+sin x cos x - cos^2 x=1`.

Lahendus. Kirjutame paremale poolele `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x',

`2 sin^2 x+sin x cos x - cos^2 x -` ` sin^2 x - cos^2 x=0`

`sin^2 x+sin x cos x - 2 cos^2 x=0`.

See on teise astme homogeenne trigonomeetriline võrrand, jagades selle vasaku ja parema osa `cos^2 x \ne 0`ga, saame:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) - \frac(2 cos^2 x)(cos^2 x)=0

"tg^2 x+tg x - 2=0". Tutvustame asendust `tg x=t`, mille tulemusena `t^2 + t - 2=0`. Selle võrrandi juured on "t_1=-2" ja "t_2=1". Seejärel:

1. „tg x=-2”, „x_1=arctg (-2)+\pi n”, „n \in Z”
2. „tg x=1”, „x=arctg 1+\pi n”, „x_2=\pi/4+\pi n”, „n \in Z”.

Vastus. `x_1=arctg (-2)+\pi n`, `n \in Z, `x_2=\pi/4+\pi n`, `n \in Z.

Minge poolnurka

Näide. Lahendage võrrand: "11 sin x - 2 cos x = 10".

Lahendus. Topeltnurga valemeid rakendades on tulemus: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`

„4 tg^2 x/2 – 11 tg x/2 +6=0”.

Kasutades ülalkirjeldatud algebralist meetodit, saame:

1. „tg x/2=2”, „x_1=2 arctg 2+2\pi n”, „n \in Z”,
2. „tg x/2=3/4”, „x_2=arctg 3/4+2\pi n”, „n \in Z”.

Vastus. `x_1=2 arctg 2+2\pi n, n \in Z, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Abinurga sissejuhatus

Trigonomeetrilises võrrandis `a sin x + b cos x =c`, kus a,b,c on koefitsiendid ja x on muutuja, jagame mõlemad osad `sqrt (a^2+b^2)-ga:

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) +b^2))".

Vasakpoolsetel koefitsientidel on siinuse ja koosinuse omadused, nimelt on nende ruutude summa võrdne 1-ga ja moodul ei ole suurem kui 1. Tähistage neid järgmiselt: `\frac a(sqrt (a^2+ b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2))= C`, siis:

`cos \varphi sin x + sin \varphi cos x =C`.

Vaatame lähemalt järgmist näidet:

Näide. Lahendage võrrand: `3 sin x+4 cos x=2`.

Lahendus. Jagades võrrandi mõlemad pooled `sqrt (3^2+4^2)`ga, saame:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))".

„3/5 sin x+4/5 cos x=2/5”.

Tähistage "3/5 = cos \varphi" , "4/5 = sin \varphi". Kuna `sin \varphi>0`, `cos \varphi>0`, võtame abinurgaks `\varphi=arcsin 4/5`. Seejärel kirjutame oma võrdsuse kujul:

`cos \varphi sin x+sin \varphi cos x=2/5`

Rakendades siinuse nurkade summa valemit, kirjutame oma võrdsuse järgmisel kujul:

`sin(x+\varphi)=2/5',

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z',

`x=(-1)^n arcsin 2/5-` `artsin 4/5+ \pi n`, `n \in Z'.

Vastus. `x=(-1)^n arcsin 2/5-` `artsin 4/5+ \pi n`, `n \in Z'.

Murdratsionaaltrigonomeetrilised võrrandid

Need on murdudega võrdsused, mille lugejates ja nimetajates on trigonomeetrilised funktsioonid.

Näide. Lahenda võrrand. `\frac (sin x)(1+cos x)=1-cos x.

Lahendus. Korrutage ja jagage võrrandi parem pool arvuga „(1+cos x)”. Selle tulemusena saame:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)

`\frac (sin x)(1+cos x)-` \frac (sin^2 x)(1+cos x)=0

`\frac (sin x-sin^2 x)(1+cos x)=0

Arvestades, et nimetaja ei saa olla null, saame `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z.

Võrdsusta murru lugeja nulliga: "sin x-sin^2 x=0", "sin x(1-sin x)=0". Seejärel „sin x=0” või „1-sin x=0”.

1. „sin x=0”, „x=\pi n”, „n \in Z”.
2. „1-sin x=0”, „sin x=-1”, „x=\pi /2+2\pi n, n \in Z”.

Arvestades, et x \ne \pi+2\pi n, n \in Z, on lahendused `x=2\pi n, n \in Z` ja `x=\pi /2+2\pi n` , 'n \in Z'.

Vastus. "x=2\pi n", "n \in Z", "x=\pi /2+2\pi n", "n \in Z".

Trigonomeetriat ja eriti trigonomeetrilisi võrrandeid kasutatakse peaaegu kõigis geomeetria, füüsika ja tehnika valdkondades. Õppetöö algab 10. klassist, eksamil on alati ülesanded, nii et proovige meeles pidada kõiki trigonomeetriliste võrrandite valemeid - need tulevad teile kindlasti kasuks!

Kuid te ei pea neid isegi pähe õppima, peamine on mõista olemust ja osata järeldada. See pole nii raske, kui tundub. Vaadake videot vaadates ise.

Videokursus "Saada A" sisaldab kõiki matemaatika eksami edukaks sooritamiseks vajalikke teemasid 60-65 punktiga. Täielikult kõik profiili ülesanded 1-13 KASUTADA matemaatikas. Sobib ka matemaatika Basic USE läbimiseks. Kui soovid sooritada eksami 90-100 punktiga, tuleb 1. osa lahendada 30 minutiga ja vigadeta!

Ettevalmistuskursus eksamiks 10-11 klassidele, samuti õpetajatele. Kõik vajalik matemaatika eksami 1. osa (esimesed 12 ülesannet) ja 13. ülesande (trigonomeetria) lahendamiseks. Ja see on ühtsel riigieksamil rohkem kui 70 punkti ja ilma nendeta ei saa hakkama ei sajapalline tudeng ega humanist.

Kogu vajalik teooria. Kiired viisid eksami lahendused, lõksud ja saladused. Kõik 1. osa asjakohased ülesanded FIPI ülesannete pangast on analüüsitud. Kursus vastab täielikult USE-2018 nõuetele.

Kursus sisaldab 5 suurt teemat, igaüks 2,5 tundi. Iga teema on antud nullist, lihtsalt ja selgelt.

Sajad eksamiülesanded. Tekstülesanded ja tõenäosusteooria. Lihtsad ja kergesti meeldejäävad probleemide lahendamise algoritmid. Geomeetria. Teooria, teatmematerjal, igat tüüpi USE ülesannete analüüs. Stereomeetria. Kavalad nipid lahendamiseks, kasulikud petulehed, ruumilise kujutlusvõime arendamine. Trigonomeetria nullist – ülesandeni 13. Tuupimise asemel mõistmine. Keeruliste mõistete visuaalne selgitus. Algebra. Juured, astmed ja logaritmid, funktsioon ja tuletis. Eksami 2. osa keeruliste ülesannete lahendamise alus.

Teie privaatsus on meile oluline. Sel põhjusel oleme välja töötanud privaatsuspoliitika, mis kirjeldab, kuidas me teie teavet kasutame ja säilitame. Palun lugege meie privaatsuspoliitikat ja andke meile teada, kui teil on küsimusi.

Isikuandmete kogumine ja kasutamine

Isikuandmed viitavad andmetele, mida saab kasutada konkreetse isiku tuvastamiseks või temaga ühenduse võtmiseks.

Teil võidakse paluda esitada oma isikuandmed igal ajal, kui võtate meiega ühendust.

Järgnevalt on toodud mõned näited, millist tüüpi isikuandmeid võime koguda ja kuidas seda teavet kasutada.

Milliseid isikuandmeid me kogume:

• Kui esitate saidil avalduse, võime koguda erinevat teavet, sealhulgas teie nime, telefoninumbrit, e-posti aadressi jne.

Kuidas me teie isikuandmeid kasutame:

• Kogutavad isikuandmed võimaldavad meil teiega ühendust võtta ja teid teavitada ainulaadsetest pakkumistest, tutvustustest ja muudest sündmustest ning eelseisvatest sündmustest.
• Aeg-ajalt võime kasutada teie isikuandmeid teile oluliste teadete ja sõnumite saatmiseks.
• Võime kasutada isikuandmeid ka sisemistel eesmärkidel, näiteks auditite, andmeanalüüsi ja erinevate uuringute läbiviimiseks, et täiustada pakutavaid teenuseid ja anda teile soovitusi meie teenuste kohta.
• Kui osalete loosimises, võistluses või sarnases stiimulis, võime kasutada teie esitatud teavet selliste programmide haldamiseks.

Avalikustamine kolmandatele isikutele

Me ei avalda teilt saadud teavet kolmandatele isikutele.

Erandid:

• Kui see on vajalik - vastavalt seadusele, kohtukorraldusele, kohtumenetluses ja/või Vene Föderatsiooni territooriumil asuvate avalike taotluste või riigiasutuste taotluste alusel - avaldage oma isikuandmed. Samuti võime avaldada teie kohta teavet, kui leiame, et selline avaldamine on vajalik või asjakohane turvalisuse, õiguskaitse või muude avalike huvide tõttu.
• Ümberkorraldamise, ühinemise või müügi korral võime edastada kogutud isikuandmed vastavale kolmandale isikule õigusjärglasele.

Isikuandmete kaitse

Me rakendame ettevaatusabinõusid – sealhulgas administratiivseid, tehnilisi ja füüsilisi –, et kaitsta teie isikuandmeid kaotsimineku, varguse ja väärkasutuse, samuti volitamata juurdepääsu, avalikustamise, muutmise ja hävitamise eest.

Teie privaatsuse säilitamine ettevõtte tasandil

Teie isikuandmete turvalisuse tagamiseks edastame oma töötajatele privaatsus- ja turvatavade ning rakendame rangelt privaatsuspõhimõtteid.