जाली गुणन विधि। शोध कार्य "गुणन के असामान्य तरीके। हिंदू विरासत

एमओयू "कुरोव्स्काया सेकेंडरी स्कूल नंबर 6"

विषय पर गणित पर सार:

« असामान्य गुणन के तरीके».

6 "बी" कक्षा के छात्र द्वारा पूरा किया गया

क्रेस्टनिकोव वसीली।

पर्यवेक्षक:

स्मिरनोवा तात्याना व्लादिमीरोवना

परिचय…………………………………………………………………………2

मुख्य हिस्सा। असामान्य तरीकेगुणन ………………… 3

2.1. थोड़ा सा इतिहास……………………………………………………..3

2.2. उंगलियों पर गुणा…………………………………………………4

2.3. 9 से गुणा ………………………………………………………………………5

2.4. गुणन का भारतीय तरीका…………………………………………….6

2.5. "लिटिल कैसल" विधि द्वारा गुणा …………………………………………… 7

2.6. "ईर्ष्या" विधि द्वारा गुणा……………………………………8

2.7. गुणन का किसान तरीका ……………………………………………..9

2.8 नया तरीका………………………………………………………..10

निष्कर्ष………………………………………………………………… 11

सन्दर्भ ……………………………………………………….1 2

मैं. परिचय.

एक व्यक्ति के लिए दैनिक जीवन में गणना के बिना करना असंभव है। इसलिए, गणित के पाठों में, हमें सबसे पहले संख्याओं पर संक्रियाएँ करना, अर्थात् गिनना सिखाया जाता है। हम स्कूल में पढ़ने वाले प्रत्येक व्यक्ति के लिए सामान्य तरीके से गुणा, भाग, जोड़ और घटाव करते हैं।

एक बार मुझे गलती से एस.एन. ओलेखनिका, यू.वी. नेस्टरेंको और एम.के. पोटापोव की एक किताब मिली "पुरानी मनोरंजक समस्याएं।" इस पुस्तक के माध्यम से, मेरा ध्यान "उंगलियों पर गुणन" नामक एक पृष्ठ की ओर आकर्षित हुआ। यह पता चला कि आप न केवल उसी तरह गुणा कर सकते हैं जैसे वे हमें गणित की पाठ्यपुस्तकों में प्रदान करते हैं। मैं सोच रहा था कि गणना करने के कोई अन्य तरीके हैं या नहीं। आखिरकार, जल्दी से गणना करने की क्षमता स्पष्ट रूप से आश्चर्यजनक है।

आधुनिक का निरंतर उपयोग कंप्यूटर विज्ञानइस तथ्य की ओर ले जाता है कि छात्रों को टेबल या गणना मशीन के बिना कोई गणना करना मुश्किल लगता है। सरलीकृत गणना तकनीकों का ज्ञान न केवल मन में सरल गणनाओं को शीघ्रता से करना संभव बनाता है, बल्कि यंत्रीकृत गणनाओं के परिणामस्वरूप त्रुटियों को नियंत्रित, मूल्यांकन, खोजने और ठीक करने के लिए भी संभव बनाता है। इसके अलावा, कम्प्यूटेशनल कौशल का विकास स्मृति विकसित करता है, सोच की गणितीय संस्कृति के स्तर को बढ़ाता है, भौतिक और गणितीय चक्र के विषयों को पूरी तरह से आत्मसात करने में मदद करता है।

उद्देश्य:

असामान्य दिखाएंगुणन के तरीके।

कार्य:

अधिक से अधिक खोजेंकंप्यूटिंग के असामान्य तरीके।

उन्हें लागू करना सीखें।

उन लोगों की तुलना में अपने लिए सबसे दिलचस्प या आसान चुनेंकी पेशकश कीस्कूल में, और गिनते समय उनका उपयोग करें।

द्वितीय. मुख्य हिस्सा। गुणन के असामान्य तरीके।

2.1. इतिहास का हिस्सा।

गणना की जिन विधियों का हम अब उपयोग करते हैं, वे हमेशा इतनी सरल और सुविधाजनक नहीं थीं। पुराने दिनों में, अधिक बोझिल और धीमी विधियों का उपयोग किया जाता था। और अगर 21वीं सदी का कोई स्कूली छात्र पांच शताब्दियों की यात्रा कर सकता है, तो वह हमारे पूर्वजों को अपनी गणना की गति और सटीकता से प्रभावित करेगा। उसके बारे में अफवाह आसपास के स्कूलों और मठों में फैल गई होगी, उस युग के सबसे कुशल काउंटरों की महिमा को ग्रहण करते हुए, और लोग नए महान गुरु के साथ अध्ययन करने के लिए आते थे।

पुराने दिनों में गुणन और भाग के संचालन विशेष रूप से कठिन थे। उस समय, प्रत्येक क्रिया के लिए अभ्यास द्वारा कोई एक तकनीक विकसित नहीं की गई थी। इसके विपरीत, एक ही समय में गुणा और भाग के लगभग एक दर्जन विभिन्न तरीकों का उपयोग किया जा रहा था - एक से अधिक जटिल तरीके, जो औसत क्षमता वाले व्यक्ति को याद नहीं रख सकते थे। प्रत्येक कलन शिक्षक ने अपनी पसंदीदा पद्धति को रखा, प्रत्येक "विभाजन के मास्टर" (ऐसे विशेषज्ञ थे) ने इस क्रिया को करने के अपने तरीके की प्रशंसा की।

वी। बेल्युस्टिन की पुस्तक में "कैसे लोग धीरे-धीरे वास्तविक अंकगणित में आए", गुणन के 27 तरीकों को रेखांकित किया गया है, और लेखक नोट करता है: "यह बहुत संभव है कि पुस्तक डिपॉजिटरी के अवकाश में और भी तरीके छिपे हों, जो कई में बिखरे हुए हों। , मुख्य रूप से हस्तलिखित संग्रह।"

और गुणन के ये सभी तरीके - "शतरंज या अंग", "झुकना", "क्रॉस", "जाली", "बैक टू फ्रंट", "डायमंड" और अन्य एक दूसरे के साथ प्रतिस्पर्धा करते थे और बड़ी मुश्किल से आत्मसात किए गए थे।

आइए गुणा के सबसे दिलचस्प और सरल तरीकों को देखें।

2.2. उंगली गुणा।

उंगलियों पर गुणा करने की प्राचीन रूसी विधि सबसे आम तरीकों में से एक है जिसे रूसी व्यापारियों ने कई शताब्दियों तक सफलतापूर्वक उपयोग किया है। उन्होंने अपनी उंगलियों पर एकल अंकों की संख्या को 6 से 9 तक गुणा करना सीखा। साथ ही, "इकाई", "जोड़े", "ट्रिपल", "फोर", " फाइव" और "दसियों"। यहां की उंगलियां एक सहायक कंप्यूटिंग डिवाइस के रूप में कार्य करती हैं।

ऐसा करने के लिए, एक तरफ उन्होंने कई उंगलियों को बढ़ाया क्योंकि पहला कारक संख्या 5 से अधिक है, और दूसरी तरफ उन्होंने दूसरे कारक के लिए भी ऐसा ही किया। बाकी उंगलियां मुड़ी हुई थीं। फिर फैली हुई उंगलियों की संख्या (कुल) ली गई और 10 से गुणा किया गया, फिर संख्याओं को गुणा करके दिखाया गया कि हाथों पर कितनी उंगलियां मुड़ी हुई थीं, और परिणाम जोड़े गए थे।

उदाहरण के लिए, आइए 7 को 8 से गुणा करें। विचार किए गए उदाहरण में, 2 और 3 उंगलियां मुड़ी हुई होंगी। यदि हम मुड़ी हुई अंगुलियों की संख्या (2+3=5) को जोड़ दें और न मुड़ी हुई उंगलियों की संख्या (2 3=6) को गुणा करें, तो हमें वांछित उत्पाद की दहाई और इकाइयों की संख्या क्रमशः 56 प्राप्त होगी। तो आप 5 से बड़ी किसी एक अंक की संख्या के गुणनफल की गणना कर सकते हैं।

2.3. 9 से गुणा करें।

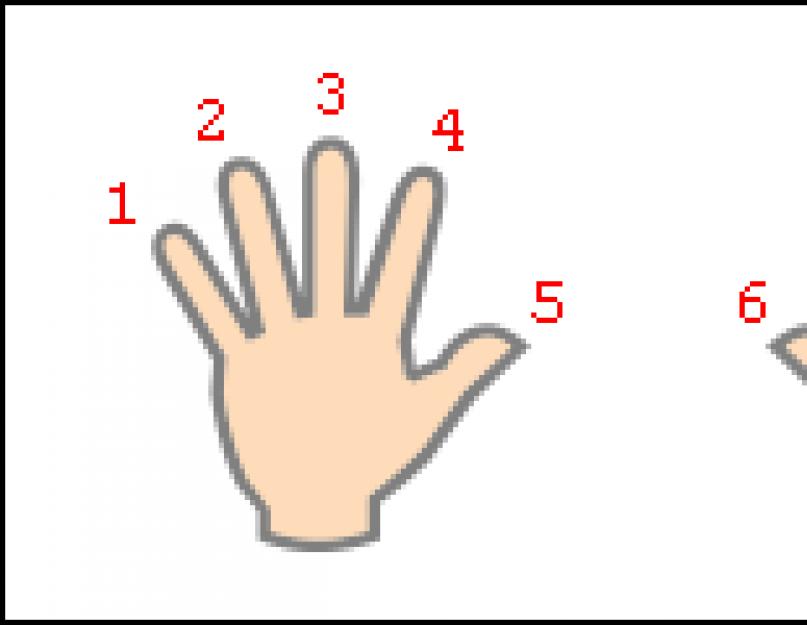
संख्या 9 . के लिए गुणन- 9 1, 9 2 ... 9 10 - स्मृति से फीका करना आसान है और इसके अलावा मैन्युअल रूप से पुनर्गणना करना अधिक कठिन है, लेकिन यह संख्या 9 के लिए है कि गुणा आसानी से "उंगलियों पर" पुन: प्रस्तुत किया जाता है। अपनी उंगलियों को दोनों हाथों पर फैलाएं और अपनी हथेलियों को अपने से दूर कर लें। बाएं हाथ की छोटी उंगली से शुरू होकर छोटी उंगली से समाप्त होने वाली उंगलियों को क्रम से 1 से 10 तक की संख्या मानसिक रूप से असाइन करें दांया हाथ(यह चित्र में दिखाया गया है)।

मान लीजिए कि हम 9 को 6 से गुणा करना चाहते हैं। हम एक उंगली को उस संख्या के बराबर मोड़ते हैं जिससे हम नौ को गुणा करेंगे। हमारे उदाहरण में, आपको उंगली को नंबर 6 से मोड़ने की जरूरत है। मुड़ी हुई उंगली के बाईं ओर की उंगलियों की संख्या हमें उत्तर में दसियों की संख्या, दाईं ओर की उंगलियों की संख्या - लोगों की संख्या दिखाती है। बाईं ओर, हमारे पास 5 उंगलियां हैं जो मुड़ी हुई नहीं हैं, दाईं ओर - 4 उंगलियां हैं। इस प्रकार, 9 6=54। नीचे दिया गया आंकड़ा "गणना" के पूरे सिद्धांत को विस्तार से दिखाता है।

एक अन्य उदाहरण: आपको 9 8=? की गणना करने की आवश्यकता है। रास्ते में, हम कहेंगे कि उंगलियां "गणना मशीन" के रूप में कार्य नहीं कर सकती हैं। उदाहरण के लिए, एक नोटबुक में 10 सेल लें। हम 8 वीं सेल को पार करते हैं। बाईं ओर 7 सेल हैं, दाईं ओर 2 सेल हैं। तो 9 8=72। सब कुछ बहुत सरल है।

7 कोशिकाएं 2 कोशिकाएं।

2.4. गुणन का भारतीय तरीका.

गणितीय ज्ञान के खजाने में सबसे मूल्यवान योगदान भारत में ही हुआ था। हिंदुओं ने प्रस्तावित किया कि जिस तरह से हम दस संकेतों का उपयोग करके संख्याएं लिखते हैं: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0।

इस पद्धति का आधार यह विचार है कि एक ही अंक इकाइयों, दहाई, सैकड़ों या हजारों के लिए है, यह इस बात पर निर्भर करता है कि यह आंकड़ा कहां है। किसी भी अंक की अनुपस्थिति में कब्जा किया गया स्थान, संख्याओं को निर्दिष्ट शून्य द्वारा निर्धारित किया जाता है।

भारतीयों ने अच्छा सोचा। वे गुणा करने का एक बहुत ही सरल तरीका लेकर आए। उन्होंने उच्चतम क्रम से शुरू करते हुए गुणन किया, और गुणक के ठीक ऊपर अधूरे उत्पादों को थोड़ा-थोड़ा करके लिखा। उसी समय, पूरे उत्पाद का वरिष्ठ अंक तुरंत दिखाई दे रहा था और इसके अलावा, किसी भी अंक की चूक को बाहर रखा गया था। गुणन चिह्न अभी तक ज्ञात नहीं था, इसलिए उन्होंने गुणनखंडों के बीच थोड़ी दूरी छोड़ दी। उदाहरण के लिए, आइए उन्हें 537 से 6 से गुणा करें:

(5 ∙ 6 =30) 30

(300 + 3 ∙ 6 = 318) 318

(3180 +7 ∙ 6 = 3222) 3222

2.5 . गुणा तरीका"लिटिल कैसल".

संख्याओं के गुणन का अध्ययन अब स्कूल की पहली कक्षा में किया जाता है। लेकिन मध्य युग में, बहुत कम लोगों ने गुणन की कला में महारत हासिल की। एक दुर्लभ अभिजात वर्ग गुणन तालिका को जानने का दावा कर सकता है, भले ही उसने यूरोपीय विश्वविद्यालय से स्नातक किया हो।

गणित के विकास के सहस्राब्दियों में, संख्याओं को गुणा करने के कई तरीकों का आविष्कार किया गया है। इतालवी गणितज्ञ लुका पसिओली ने अपने ग्रंथ "अंकगणित, अनुपात और आनुपातिकता में ज्ञान का योग" (1494) में गुणन के आठ अलग-अलग तरीके दिए हैं। उनमें से पहले को "लिटिल कैसल" कहा जाता है, और दूसरा कोई कम रोमांटिक नहीं है जिसे "ईर्ष्या या जाली गुणन" कहा जाता है।

"लिटिल कैसल" गुणन पद्धति का लाभ यह है कि उच्चतम अंकों के अंक शुरुआत से ही निर्धारित किए जाते हैं, और यह महत्वपूर्ण हो सकता है यदि आपको मूल्य का जल्दी से अनुमान लगाने की आवश्यकता है।

सबसे महत्वपूर्ण अंक से शुरू होने वाली ऊपरी संख्या के अंकों को वैकल्पिक रूप से निचली संख्या से गुणा किया जाता है और शून्य की आवश्यक संख्या के अतिरिक्त एक कॉलम में लिखा जाता है। फिर परिणाम जोड़े जाते हैं।

2.6. संख्या गुणनईर्ष्या विधि।

दूसरी विधि को रोमांटिक रूप से "ईर्ष्या" या "जाली गुणन" कहा जाता है।

सबसे पहले, एक आयत खींचा जाता है, जिसे वर्गों में विभाजित किया जाता है, और आयत के पक्षों के आयाम गुणक और गुणक के लिए दशमलव स्थानों की संख्या के अनुरूप होते हैं। फिर वर्ग कोशिकाओं को तिरछे विभाजित किया जाता है, और "... यह एक तस्वीर निकलती है जो जाली शटर, अंधा की तरह दिखती है," पैसीओली लिखते हैं। "ऐसे शटर विनीशियन घरों की खिड़कियों पर लटकाए गए थे, जो राहगीरों को खिड़कियों पर बैठी महिलाओं और ननों को देखने से रोकते थे।"

आइए इस तरह से 347 को 29 से गुणा करें। आइए एक टेबल बनाएं, उसके ऊपर 347 नंबर और दाईं ओर 29 नंबर लिखें।

प्रत्येक पंक्ति में हम इस सेल के ऊपर और उसके दाईं ओर संख्याओं का उत्पाद लिखते हैं, जबकि उत्पाद के दसियों की संख्या स्लैश के ऊपर लिखी जाती है, और इकाइयों की संख्या इसके नीचे होती है। अब इस ऑपरेशन को दाएं से बाएं करके प्रत्येक स्लैश में संख्याओं को जोड़ें। यदि राशि 10 से कम है, तो हम इसे बैंड के नीचे की संख्या के नीचे लिखते हैं। यदि यह 10 से अधिक हो जाता है, तो हम योग की केवल इकाइयों की संख्या लिखते हैं, और दसियों की संख्या को अगली राशि में जोड़ते हैं। नतीजतन, हमें वांछित उत्पाद 10063 मिलता है।

2.7. प्रतिगुणन का देहाती तरीका.

सबसे ज्यादा, मेरी राय में, "देशी" और आसान तरीकागुणन रूसी किसानों द्वारा उपयोग की जाने वाली विधि है। इस तकनीक में आम तौर पर संख्या 2 से आगे गुणन तालिका के ज्ञान की आवश्यकता नहीं होती है। इसका सार यह है कि किन्हीं दो संख्याओं के गुणन को एक संख्या के क्रमिक विभाजनों की श्रृंखला में आधा कर दिया जाता है जबकि दूसरी संख्या को दोगुना कर दिया जाता है। समद्विभाजन तब तक जारी रहता है जब तक कि भागफल 1 न हो जाए, जबकि समानांतर में दूसरी संख्या को दोगुना कर दिया जाए। अंतिम दोगुनी संख्या वांछित परिणाम देती है।

एक विषम संख्या के मामले में, इकाई को छोड़ देना चाहिए और शेष को आधे में विभाजित करना चाहिए; लेकिन दूसरी ओर, दाएं कॉलम की अंतिम संख्या में इस कॉलम के उन सभी नंबरों को जोड़ना आवश्यक होगा जो बाएं कॉलम की विषम संख्याओं के विपरीत हैं: योग वांछित उत्पाद होगा

संगत संख्याओं के सभी युग्मों का गुणनफल समान होता है, इसलिए

37 ∙ 32 = 1184 ∙ 1 = 1184

उस स्थिति में जब संख्याओं में से एक विषम हो या दोनों संख्याएँ विषम हों, इस प्रकार आगे बढ़ें:

384 ∙ 1 = 384

24 ∙ 17 = 24∙(16+1)=24 ∙ 16 + 24 = 384 + 24 = 408

2.8 . गुणा करने का एक नया तरीका।

दिलचस्पगुणन का एक नया तरीका जो हाल ही में बताया गया है। आविष्कारक नई प्रणालीमौखिक गणना के, दर्शनशास्त्र में पीएच.डी. वासिली ओकोनेशनिकोव का तर्क है कि एक व्यक्ति बड़ी मात्रा में जानकारी को याद रखने में सक्षम है, मुख्य बात यह है कि इस जानकारी को कैसे व्यवस्थित किया जाए। स्वयं वैज्ञानिक के अनुसार, नौ-दशमलव प्रणाली इस संबंध में सबसे अधिक लाभप्रद है - सभी डेटा को कैलकुलेटर पर बटन की तरह व्यवस्थित नौ कोशिकाओं में रखा जाता है।

ऐसी तालिका के अनुसार गिनना बहुत आसान है। उदाहरण के लिए, आइए संख्या 15647 को 5 से गुणा करें। पांच से संबंधित तालिका के भाग में, हम क्रम में संख्या के अंकों के अनुरूप संख्याओं का चयन करते हैं: एक, पांच, छह, चार और सात। हमें मिलता है: 05 25 30 20 35

बाईं संख्या (हमारे उदाहरण में, शून्य) को अपरिवर्तित छोड़ दिया जाता है, और निम्नलिखित संख्याओं को जोड़े में जोड़ा जाता है: पांच दो के साथ, पांच तीन के साथ, शून्य दो के साथ, शून्य तीन के साथ। अंतिम अंक भी अपरिवर्तित है।

परिणामस्वरूप, हम प्राप्त करते हैं: 078235। संख्या 78235 गुणन का परिणाम है।

यदि दो अंकों को जोड़ने पर नौ से अधिक की संख्या प्राप्त होती है, तो परिणाम के पिछले अंक में उसका पहला अंक जोड़ा जाता है, और दूसरा "उसके" स्थान पर लिखा जाता है।

तृतीय. निष्कर्ष।

गिनती के सभी असामान्य तरीकों में से, "जाली गुणन या ईर्ष्या" की विधि सबसे दिलचस्प लग रही थी। मैंने इसे अपने सहपाठियों को दिखाया और उन्हें भी यह बहुत पसंद आया।

सबसे आसान तरीका मुझे रूसी किसानों द्वारा इस्तेमाल किया जाने वाला "दोगुना और बंटवारा" तरीका लगा। मैं इसका उपयोग बहुत बड़ी संख्याओं को गुणा करते समय करता हूं (दो अंकों की संख्याओं को गुणा करते समय इसका उपयोग करना बहुत सुविधाजनक होता है)।

मुझे गुणा के एक नए तरीके में दिलचस्पी थी, क्योंकि यह आपको अपने दिमाग में बड़ी संख्या में "बारी" करने की अनुमति देता है।

मुझे लगता है कि एक कॉलम से गुणा करने का हमारा तरीका भी सही नहीं है, और हम और भी तेज और अधिक विश्वसनीय तरीके के साथ आ सकते हैं।

साहित्य।

डेपमैन आई। "गणित के बारे में कहानियां"। - लेनिनग्राद।: शिक्षा, 1954. - 140 पी।

कोर्निव ए.ए. रूसी गुणन की घटना। कहानी। http://numbernautics.ru/

ओलेखनिक एस.एन., नेस्टरेंको यू.वी., पोतापोव एम.के. "पुरानी मनोरंजक समस्याएं।" - एम .: विज्ञान। भौतिक और गणितीय साहित्य का मुख्य संस्करण, 1985. - 160 पी.

पेरेलमैन वाई.आई. त्वरित खाता। मानसिक गणना की तीस सरल विधियाँ। एल।, 1941 - 12 पी।

पेरेलमैन वाई.आई. मनोरंजक अंकगणित। एम. रुसानोवा, 1994-205पी।

विश्वकोश “मैं दुनिया को जानता हूं। गणित"। - एम .: एस्ट्रेल एर्मक, 2004।

बच्चों के लिए विश्वकोश। "गणित"। - एम .: अवंता +, 2003. - 688 पी।

नॉलेज बेस में अपना अच्छा काम भेजें सरल है। नीचे दिए गए फॉर्म का प्रयोग करें

छात्र, स्नातक छात्र, युवा वैज्ञानिक जो अपने अध्ययन और कार्य में ज्ञान आधार का उपयोग करते हैं, वे आपके बहुत आभारी रहेंगे।

प्रकाशित किया गया http://www.allbest.ru/

बहु-अंकीय संख्याओं के गुणन के मूल तरीके और गणित के पाठों में उनके आवेदन की संभावना

पर्यवेक्षक:

शशकोवा एकातेरिना ओलेगोवन

परिचय

1. थोड़ा सा इतिहास

2. उंगलियों पर गुणन

3. 9 . से गुणा करें

4. गुणन का भारतीय तरीका

5. "लिटिल कैसल" विधि का उपयोग करके गुणा करें

6. "ईर्ष्या" की विधि से गुणा

7. गुणन का किसान तरीका

8. गुणा करने का एक नया तरीका

निष्कर्ष

साहित्य

परिचय

एक बार मुझे गलती से एस.एन. ओलेखनिका, यू.वी. नेस्टरेंको और एम.के. पोटापोव "पुरानी मनोरंजक समस्याएं"। इस पुस्तक के माध्यम से, मेरा ध्यान "उंगलियों पर गुणन" नामक एक पृष्ठ की ओर आकर्षित हुआ। यह पता चला कि आप न केवल उसी तरह गुणा कर सकते हैं जैसे वे हमें गणित की पाठ्यपुस्तकों में प्रदान करते हैं। मैं सोच रहा था कि गणना करने के कोई अन्य तरीके हैं या नहीं। आखिरकार, जल्दी से गणना करने की क्षमता स्पष्ट रूप से आश्चर्यजनक है।

आधुनिक कंप्यूटिंग तकनीक का निरंतर उपयोग इस तथ्य की ओर ले जाता है कि छात्रों को टेबल या गणना मशीन के बिना कोई गणना करना मुश्किल लगता है। सरलीकृत गणना तकनीकों का ज्ञान न केवल मन में सरल गणनाओं को शीघ्रता से करना संभव बनाता है, बल्कि यंत्रीकृत गणनाओं के परिणामस्वरूप त्रुटियों को नियंत्रित, मूल्यांकन, खोजने और ठीक करने के लिए भी संभव बनाता है। इसके अलावा, कम्प्यूटेशनल कौशल का विकास स्मृति विकसित करता है, सोच की गणितीय संस्कृति के स्तर को बढ़ाता है, भौतिक और गणितीय चक्र के विषयों को पूरी तरह से आत्मसात करने में मदद करता है।

उद्देश्य:

असामान्य दिखाएं गुणन के तरीके।

कार्य:

वू अधिक से अधिक खोजें कंप्यूटिंग के असामान्य तरीके।

उनका उपयोग करना सीखें।

अपने लिए स्कूल में पेश किए जाने वाले लोगों की तुलना में सबसे दिलचस्प या आसान चुनें, और गिनती करते समय उनका उपयोग करें।

1. इतिहास का हिस्सा

और ये सभी गुणन तकनीकें - "शतरंज या अंग", "झुकना", "क्रॉस", "जाली", "बैक टू फ्रंट", "डायमंड" और अन्य ने एक-दूसरे के साथ प्रतिस्पर्धा की और बड़ी मुश्किल से आत्मसात किया।

आइए गुणा के सबसे दिलचस्प और सरल तरीकों को देखें।

2. उंगलियों पर गुणन

उदाहरण के लिए, आइए 7 को 8 से गुणा करें। विचार किए गए उदाहरण में, 2 और 3 उंगलियां मुड़ी हुई होंगी। यदि हम मुड़ी हुई उंगलियों की संख्या (2+3=5) को जोड़ दें और मुड़ी हुई उंगलियों की संख्या (2*3=6) को गुणा करें, तो हमें वांछित उत्पाद की दहाई और इकाइयों की संख्या क्रमशः 56 प्राप्त होगी। तो आप 5 से बड़ी किसी एक अंक की संख्या के गुणनफल की गणना कर सकते हैं।

3. 9 . से गुणा करें

संख्या 9 . के लिए गुणन- 9 1, 9 2 ... 9 10 - स्मृति से फीका करना आसान है और इसके अलावा मैन्युअल रूप से पुनर्गणना करना अधिक कठिन है, लेकिन यह संख्या 9 के लिए है कि गुणा आसानी से "उंगलियों पर" पुन: प्रस्तुत किया जाता है। अपनी उंगलियों को दोनों हाथों पर फैलाएं और अपनी हथेलियों को अपने से दूर कर लें। बाएं हाथ की छोटी उंगली से शुरू होकर दाहिने हाथ की छोटी उंगली से समाप्त होने वाली उंगलियों को मानसिक रूप से 1 से 10 तक की संख्या दें (यह चित्र में दिखाया गया है)।

मान लीजिए कि हम 9 को 6 से गुणा करना चाहते हैं। हम एक उंगली को उस संख्या के बराबर मोड़ते हैं जिससे हम नौ को गुणा करेंगे। हमारे उदाहरण में, आपको उंगली को नंबर 6 से मोड़ने की जरूरत है। मुड़ी हुई उंगली के बाईं ओर की उंगलियों की संख्या हमें उत्तर में दसियों की संख्या, दाईं ओर की उंगलियों की संख्या - लोगों की संख्या दिखाती है। बाईं ओर, हमारे पास 5 उंगलियां हैं जो मुड़ी हुई नहीं हैं, दाईं ओर - 4 उंगलियां हैं। इस प्रकार, 9 6=54। नीचे दिया गया आंकड़ा संपूर्ण "गणना" सिद्धांत को विस्तार से दिखाता है।

एक अन्य उदाहरण: आपको 9 8=? की गणना करने की आवश्यकता है। रास्ते में, हम कहेंगे कि उंगलियां जरूरी नहीं कि "गणना मशीन" के रूप में कार्य करें। उदाहरण के लिए, एक नोटबुक में 10 सेल लें। हम 8 वीं सेल को पार करते हैं। बाईं ओर 7 सेल हैं, दाईं ओर 2 सेल हैं। तो 9 8=72। सब कुछ बहुत सरल है। गुणन की विधि सरलीकृत रोचक

4. गुणन का भारतीय तरीका

5. गुणाबिल्कुल नहीं"लिटिल कैसल"

गणित के विकास के सहस्राब्दियों में, संख्याओं को गुणा करने के कई तरीकों का आविष्कार किया गया है। इतालवी गणितज्ञ लुका पैसिओली ने अपने ग्रंथ द सम ऑफ नॉलेज इन अरिथमेटिक, रिलेशंस एंड प्रॉपोनैलिटी (1494) में गुणन के आठ अलग-अलग तरीकों की सूची दी है। उनमें से पहले को "लिटिल कैसल" कहा जाता है, और दूसरा कोई कम रोमांटिक नहीं है जिसे "ईर्ष्या या जाली गुणन" कहा जाता है।

6. स्मार्टनंबरतरीका "ईर्ष्या द्वेष»

दूसरी विधि को रोमांटिक रूप से "ईर्ष्या" या "जाली गुणन" कहा जाता है।

7 . प्रतिगुणन का देहाती तरीका

मेरी राय में, "मूल" और गुणन का आसान तरीका रूसी किसानों द्वारा उपयोग की जाने वाली विधि है। इस तकनीक में आम तौर पर संख्या 2 से आगे गुणन तालिका के ज्ञान की आवश्यकता नहीं होती है। इसका सार यह है कि किन्हीं दो संख्याओं के गुणन को एक संख्या के क्रमिक विभाजनों की श्रृंखला में आधा कर दिया जाता है जबकि दूसरी संख्या को दोगुना कर दिया जाता है। समद्विभाजन तब तक जारी रहता है जब तक कि भागफल 1 न हो जाए, जबकि समानांतर में दूसरी संख्या को दोगुना कर दिया जाए। अंतिम दोगुनी संख्या वांछित परिणाम देती है।

संगत संख्याओं के सभी युग्मों का गुणनफल समान होता है, इसलिए

37 32 = 1184 1 = 1184

24 17 = 24 (16+1)=24 16 + 24 = 384 + 24 = 408

8 . गुणा करने का नया तरीका

हाल ही में गुणा करने का एक दिलचस्प नया तरीका बताया गया है। नई मानसिक गणना प्रणाली के आविष्कारक वसीली ओकोनेशनिकोव, दर्शनशास्त्र में पीएचडी, का दावा है कि एक व्यक्ति बड़ी मात्रा में जानकारी को याद रखने में सक्षम है, मुख्य बात यह है कि इस जानकारी को कैसे व्यवस्थित किया जाए। स्वयं वैज्ञानिक के अनुसार, नौ-दशमलव प्रणाली इस संबंध में सबसे अधिक लाभप्रद है - सभी डेटा को कैलकुलेटर पर बटन की तरह व्यवस्थित नौ कोशिकाओं में रखा जाता है।

बायां अंक (हमारे उदाहरण में, शून्य) अपरिवर्तित रहता है, और निम्नलिखित संख्याओं को जोड़े में जोड़ा जाता है: पांच दो के साथ, पांच तीन के साथ, शून्य दो के साथ, शून्य तीन के साथ। अंतिम अंक भी अपरिवर्तित है।

परिणामस्वरूप, हम प्राप्त करते हैं: 078235। संख्या 78235 गुणन का परिणाम है।

साहित्य

1. डेपमैन आई। "गणित के बारे में कहानियां।" - लेनिनग्राद।: शिक्षा, 1954. - 140 पी।

2. कोर्निव ए.ए. रूसी गुणन की घटना। कहानी। http://numbernautics.ru/

3. ओलेखनिक एस। एन।, नेस्टरेंको यू। वी।, पोटापोव एम। के। "पुरानी मनोरंजक समस्याएं।" - एम .: विज्ञान। भौतिक और गणितीय साहित्य का मुख्य संस्करण, 1985. - 160 पी.

4. पेरेलमैन वाई.आई. त्वरित खाता। मानसिक गणना की तीस सरल विधियाँ। एल।, 1941 - 12 पी।

5. पेरेलमैन वाई.आई. मनोरंजक अंकगणित। एम. रुसानोवा, 1994--205पी।

6. विश्वकोश “मैं दुनिया को जानता हूं। गणित"। - एम .: एस्ट्रेल एर्मक, 2004।

7. बच्चों के लिए विश्वकोश। "गणित"। - एम .: अवंता +, 2003. - 688 पी।

Allbest.ru . पर होस्ट किया गया

...

इसी तरह के दस्तावेज़

लोगों ने गिनना कैसे सीखा, संख्याओं, संख्याओं और संख्या प्रणालियों का उदय। "उंगलियों" पर गुणन तालिका: संख्या 9 और 8 के लिए गुणन तकनीक। त्वरित गणना के उदाहरण। दो अंकों की संख्या को 11, 111, 1111 आदि से गुणा करने के तरीके। और 999 से तीन अंकों की संख्या।

टर्म पेपर, जोड़ा गया 10/22/2011

कुछ पूर्णांक मान तक अभाज्य संख्याओं की दी गई श्रृंखला से खोजने के लिए एराटोस्थनीज की चलनी की विधि का अनुप्रयोग। जुड़वां primes की समस्या पर विचार। पहली डिग्री के मूल बहुपद में जुड़वाँ अभाज्य संख्याओं की अनंतता का प्रमाण।

परीक्षण, 10/05/2010 जोड़ा गया

गुणा और भाग का परिचय। उत्पाद द्वारा राशि के प्रतिस्थापन के मामलों पर विचार। समान और भिन्न पदों वाले उदाहरणों के समाधान। विभाजन की कम्प्यूटेशनल विधि, समान भागों में विभाजन। गुणन सारणी को चंचल तरीके से पढ़ाना।

प्रस्तुति, जोड़ा गया 04/15/2015

गणित में अभाज्य संख्याओं के अर्थ के अध्ययन के इतिहास का वर्णन करते हुए कि वे कैसे पाए जाते हैं। अभाज्य संख्याओं के सिद्धांत के विकास में पिएत्रो कैटाल्डी का योगदान। एराटोस्थनीज की अभाज्य संख्याओं की तालिकाएँ संकलित करने की विधि। प्राकृतिक संख्याओं की मित्रता।

परीक्षण, 12/24/2010 जोड़ा गया

अंकगणितीय-तार्किक इकाइयों का उद्देश्य, संरचना और संरचना, उनका वर्गीकरण, प्रतिनिधित्व के साधन। ALU कंप्यूटर के निर्माण और कार्यप्रणाली के सिद्धांत। गुणन एल्गोरिथ्म के एक ब्लॉक आरेख का निर्माण, नियंत्रण संकेतों के एक सेट का निर्धारण, सर्किट डिजाइन।

टर्म पेपर, जोड़ा गया 10/25/2014

गणित में "मैट्रिक्स" की अवधारणा। किसी भी आकार के आव्यूह को एक मनमाना संख्या से गुणा (विभाजित) करने की क्रिया। दो मैट्रिक्स के गुणन का संचालन और गुण। एक ट्रांसपोज़्ड मैट्रिक्स एक मैट्रिक्स है जो मूल मैट्रिक्स से कॉलम द्वारा प्रतिस्थापित पंक्तियों के साथ प्राप्त होता है।

परीक्षण, जोड़ा गया 07/21/2010

प्राचीन काल में अभाज्य संख्याओं के अध्ययन के ऐतिहासिक तथ्य, समस्या की वर्तमान स्थिति। संख्याओं की प्राकृतिक श्रृंखला में अभाज्य संख्याओं का वितरण, उनके व्यवहार की प्रकृति और कारण। प्रतिक्रिया कानून के आधार पर जुड़वां अपराधों के वितरण का विश्लेषण।

लेख, जोड़ा गया 03/28/2012

घन समीकरणों की मूल अवधारणाएँ और परिभाषाएँ, उन्हें हल करने के तरीके। कार्डानो का सूत्र और विएटा का त्रिकोणमितीय सूत्र, गणना पद्धति का सार। घनों के अंतर के संक्षिप्त गुणन के लिए सूत्र का अनुप्रयोग। एक वर्ग ट्रिनोमियल की जड़ की परिभाषा।

टर्म पेपर, जोड़ा गया 10/21/2013

गणित में संयोजक समस्याओं के विभिन्न उदाहरणों पर विचार। संभावित विकल्पों की गणना करने के तरीकों का विवरण। संयोजन गुणन नियम का उपयोग करना। विकल्पों का पेड़ बनाना। क्रमपरिवर्तन, संयोजन, प्लेसमेंट सबसे सरल संयोजन के रूप में।

प्रस्तुति, जोड़ा गया 10/17/2015

मैट्रिक्स द्वारा दिए गए रैखिक परिवर्तन को लागू करने के परिणाम के रूप में एक मैट्रिक्स के eigenvector का निर्धारण (एक eigenvalue द्वारा एक वेक्टर को गुणा करना)। लीवरियर-फद्दीव विधि के एल्गोरिथम के ब्लॉक आरेख की मुख्य क्रियाओं और विवरण की सूची।

चार हजार साल पहले, बेबीलोनियों ने गुणन का आविष्कार किया था। और इसी साल मार्च में गणितज्ञों ने इसमें सुधार किया।

18 मार्च, 2019 को, दो शोधकर्ताओं ने दो बहुत बड़ी संख्याओं को गुणा करने के लिए सबसे तेज़ ज्ञात विधि का वर्णन किया। यह कार्य गणित के बुनियादी कार्यों में से एक को करने के लिए सबसे कुशल प्रक्रिया के लिए एक लंबे समय से खोज की परिणति का प्रतीक है।

फ्रेंच नेशनल सेंटर फॉर साइंटिफिक रिसर्च के गणितज्ञ जोरिस वैन डेर होवेन कहते हैं, "हर कोई सोचता है कि स्कूल में उन्होंने जो गुणन विधि सीखी है, वह सबसे अच्छी है, लेकिन वास्तव में इस क्षेत्र में बहुत सारे शोध चल रहे हैं।" - कागज के लेखक।

कई कम्प्यूटेशनल समस्याओं की जटिलता, के नए अंक गिनने से लेकर बड़े प्राइम खोजने तक, गुणन की गति तक कम हो जाती है। वैन डेर होवेन ने अपने परिणाम को कई अन्य समस्याओं के लिए एक प्रकार की गणितीय गति सीमा निर्दिष्ट करने के रूप में वर्णित किया है।

"भौतिकी में, प्रकाश की गति जैसे महत्वपूर्ण स्थिरांक हैं जो आपको चीजों का वर्णन करने की अनुमति देते हैं," वैन डेर होवेन ने कहा। "यदि आप यह जानना चाहते हैं कि कंप्यूटर कितनी तेजी से कुछ गणितीय समस्याओं को हल कर सकते हैं, तो पूर्णांकों का गुणन एक प्रकार के बुनियादी निर्माण खंड के रूप में सामने आता है जिसके संबंध में आप इतनी गति व्यक्त कर सकते हैं।"

लगभग हर कोई एक ही तरह से संख्याओं को गुणा करना सीखता है। हम संख्याओं को एक कॉलम में लिखते हैं, शीर्ष संख्या को नीचे के प्रत्येक अंक से गुणा करते हैं (अंकों को ध्यान में रखते हुए) और परिणाम जोड़ते हैं। दो दो अंकों की संख्याओं को गुणा करते समय, आपको अंतिम परिणाम प्राप्त करने के लिए चार छोटे गुणा करना होगा।

"स्थानांतरण" की स्कूल पद्धति के लिए n 2 चरणों की आवश्यकता होती है, जहाँ n प्रत्येक गुणा संख्या में अंकों की संख्या होती है। तीन अंकों की संख्याओं की गणना के लिए नौ गुणा की आवश्यकता होती है, और सौ अंकों की संख्या के साथ - 10,000।

कैरी विधि कुछ अंकों के साथ संख्याओं के साथ ठीक काम करती है, लेकिन लाखों या अरबों अंकों के साथ संख्याओं को गुणा करने पर यह फंस जाता है (जो कि कंप्यूटर वास्तव में पीआई की गणना करते समय या दुनिया भर में बड़े प्राइम की खोज करते समय करता है)। दो संख्याओं को एक अरब अंकों से गुणा करने के लिए एक अरब वर्ग या 10 18 गुणा की आवश्यकता होगी, जिसमें एक आधुनिक कंप्यूटर को लगभग 30 वर्ष लगेंगे।

कई सहस्राब्दियों के लिए, यह माना जाता था कि संख्याओं को तेजी से गुणा करना असंभव था। फिर, 1960 में, 23 वर्षीय सोवियत और रूसी गणितज्ञ अनातोली अलेक्सेविच करात्सुबा ने सोवियत गणितज्ञ आंद्रेई निकोलाइविच कोलमोगोरोव के नेतृत्व में एक सेमिनार में भाग लिया, जो 20वीं सदी के महानतम गणितज्ञों में से एक थे। कोलमोगोरोव ने कहा कि गुणा का कोई सामान्यीकृत तरीका नहीं है जिसके लिए n 2 से कम संचालन की आवश्यकता होती है। करत्सुबा ने फैसला किया कि ऐसा कोई रास्ता है - और एक हफ्ते की खोज के बाद, उन्होंने इसे खोज लिया।

अनातोली अलेक्सेविच करात्सुबा

करत्सुबा गुणन में एक संख्या के अंकों को विभाजित करना और उन्हें एक नए तरीके से पुनर्संयोजित करना शामिल है, जो इसके बजाय अनुमति देता है एक बड़ी संख्या मेंगुणा कम जोड़ और घटाव करते हैं। विधि समय बचाती है क्योंकि जोड़ n 2 के बजाय केवल 2n चरण लेता है।

पारंपरिक 25x63 गुणन विधि के लिए चार एकल अंकों के गुणन और कुछ जोड़ की आवश्यकता होती है।

25x63 करात्सुबा गुणन के लिए तीन एकल अंकों के गुणन और कुछ जोड़ और घटाव की आवश्यकता होती है।
ए) संख्याओं को विभाजित करना
बी) दसियों गुणा करें
सी) इकाइयों को गुणा करें
d) संख्याओं को जोड़ें
ई) इन राशियों को गुणा करें
च) गिनती ई - बी - सी
छ) b, c और f . से अंतिम योग प्राप्त करें

संख्याओं में वर्णों की संख्या में वृद्धि के साथ, करात्सुबा पद्धति का पुनरावर्ती रूप से उपयोग किया जा सकता है।

पारंपरिक 2531x1467 गुणन पद्धति के लिए 16 एकल अंकों के गुणन की आवश्यकता होती है।

करत्सुबा 2531x1467 को गुणा करने के लिए 9 गुणा की आवश्यकता होती है।

पेंसिल्वेनिया के गणितज्ञ मार्टिन फ्यूहरर ने कहा, "जोड़ना स्कूल में एक साल पहले किया जाता है क्योंकि यह बहुत आसान है, यह रैखिक समय में, बाएं से दाएं पढ़ने की गति से किया जाता है।" स्टेट यूनिवर्सिटी, जिन्होंने 2007 में उस समय का सबसे तेज गुणन एल्गोरिथम बनाया था।

बड़ी संख्या के साथ काम करते समय, करात्सुबा गुणन को पुनरावर्ती रूप से दोहराया जा सकता है, मूल संख्याओं को लगभग उतने ही भागों में विभाजित किया जा सकता है, जितने उनमें संकेत हैं। और प्रत्येक विभाजन के साथ, आप गुणा को बदलते हैं, जिसके लिए जोड़ और घटाव के लिए कई चरणों की आवश्यकता होती है, जिसके लिए बहुत कम चरणों की आवश्यकता होती है।

न्यू साउथ वेल्स विश्वविद्यालय के गणितज्ञ और नए काम के सह-लेखक डेविड हार्वे ने कहा, "कुछ गुणाओं को जोड़ में बदला जा सकता है, यह देखते हुए कि कंप्यूटर इसे तेजी से करने में सक्षम होंगे।"

करत्सुबा की विधि ने केवल n 1.58 एकल-अंकीय गुणाओं का उपयोग करके संख्याओं को गुणा करना संभव बना दिया। फिर 1971 में, अर्नोल्ड शॉनहेज और वोल्कर स्ट्रैसन ने बड़ी संख्याओं को n × log n × log(log n) छोटे गुणा में गुणा करने के लिए एक विधि प्रकाशित की। दो अरब अंकों की प्रत्येक संख्या को गुणा करने के लिए, करात्सुबा की विधि के लिए 165 ट्रिलियन चरणों की आवश्यकता होगी।

जोरिस वैन डेर होवेन, फ्रेंच नेशनल सेंटर फॉर साइंटिफिक रिसर्च के गणितज्ञ

Schönhage-Strassen पद्धति का उपयोग कंप्यूटर द्वारा बड़ी संख्या में गुणा करने के लिए किया जाता है, और इससे दो अन्य महत्वपूर्ण परिणाम सामने आए हैं। सबसे पहले, उन्होंने फास्ट फूरियर ट्रांसफॉर्म नामक सिग्नल प्रोसेसिंग तकनीक की शुरुआत की। तब से, यह तकनीक सभी तेज गुणन एल्गोरिदम का आधार रही है।

दूसरा, एक ही पेपर में, शॉनहेज और स्ट्रैसन ने एक और भी तेज़ एल्गोरिथम की संभावना का सुझाव दिया- एक ऐसी विधि जिसके लिए एक ही चिन्ह द्वारा केवल n × log n गुणा की आवश्यकता होती है- और यह कि ऐसा एल्गोरिथम सबसे तेज़ संभव होगा। यह धारणा इस भावना पर आधारित थी कि, गुणन जैसे मौलिक संचालन के लिए, संचालन की सीमा को n × log n × log(log n) की तुलना में किसी भी तरह से अधिक सुरुचिपूर्ण ढंग से लिखा जाना चाहिए।

फ्यूहरर ने कहा, "ज्यादातर आम तौर पर इस बात से सहमत होते हैं कि गुणन इतना महत्वपूर्ण बुनियादी ऑपरेशन है कि विशुद्ध रूप से सौंदर्य की दृष्टि से, इसे जटिलता पर एक अच्छी बाधा की आवश्यकता होती है।" "हम अनुभव से जानते हैं कि मूल बातें के पीछे का गणित हमेशा सुरुचिपूर्ण होता है।"

अजीब Schönhage और Strassen बाधा, n × लॉग n × लॉग (लॉग n), 36 वर्षों के लिए आयोजित किया गया। 2007 में, फ्यूहरर ने इस रिकॉर्ड को तोड़ दिया, और सब कुछ घूमने लगा। पिछले एक दशक में, गणितज्ञों ने तेजी से गुणा करने वाले एल्गोरिदम की खोज की है, जिनमें से प्रत्येक धीरे-धीरे n × log n चिह्न तक पहुंच गया है, उस तक नहीं पहुंच पाया है। फिर इसी साल मार्च में हार्वे और वैन डेर होवेन वहां पहुंचे।

उनका तरीका उनके सामने किए गए बहुत सारे कामों में सुधार है। यह संख्याओं को संकेतों में विभाजित करता है, फास्ट फूरियर ट्रांसफॉर्म के बेहतर संस्करण का उपयोग करता है, और पिछले 40 वर्षों में की गई अन्य सफलताओं का लाभ उठाता है। वैन डेर होवेन ने कहा, "हम एफएफटी का अधिक गंभीर रूप से उपयोग कर रहे हैं, इसे केवल एक बार के बजाय कई बार उपयोग कर रहे हैं, और अतिरिक्त और घटाव के साथ और भी गुणा को प्रतिस्थापित कर रहे हैं।"

हार्वे और वैन डेर होवेन का एल्गोरिथ्म साबित करता है कि गुणा n × log n चरणों में किया जा सकता है। हालांकि, यह एक तेज विधि की अनुपस्थिति को साबित नहीं करता है। यह स्थापित करना अधिक कठिन होगा कि उनका दृष्टिकोण यथासंभव तेज़ है। फरवरी के अंत में, आरहूस विश्वविद्यालय के कंप्यूटर वैज्ञानिकों की एक टीम ने एक पेपर प्रकाशित किया जिसमें कहा गया था कि यदि अप्रमाणित प्रमेयों में से एक सच हो जाता है, तो यह विधि वास्तव में गुणा करने का सबसे तेज़ तरीका होगा।

और यद्यपि यह नया एल्गोरिथ्म सिद्धांत रूप में बहुत महत्वपूर्ण है, व्यवहार में यह बहुत अधिक नहीं बदलेगा, क्योंकि यह पहले से उपयोग में आने वाले एल्गोरिदम से थोड़ा ही बेहतर प्रदर्शन करता है। वैन डेर होवेन ने कहा, "हम केवल तीन गुना गति की उम्मीद कर सकते हैं।" "अपमानजनक कुछ भी नहीं।"

इसके अलावा, कंप्यूटर उपकरण की योजनाएं बदल गई हैं। बीस साल पहले, कंप्यूटर ने गुणन की तुलना में बहुत तेजी से जोड़ का प्रदर्शन किया। गुणन और जोड़ के बीच की गति का अंतर काफी कम हो गया है, जिसके परिणामस्वरूप गुणन कुछ चिप्स पर जोड़ से आगे निकल सकता है। कुछ प्रकार के हार्डवेयर के साथ, "आप कंप्यूटर को संख्याओं को गुणा करके गति बढ़ा सकते हैं, और यह एक तरह का पागलपन है," हार्वे ने कहा।

हार्डवेयर समय के साथ बदलता है, लेकिन उनकी कक्षा में सबसे अच्छा एल्गोरिदम हमेशा के लिए रहता है। भविष्य में कंप्यूटर चाहे जो भी दिखें, हार्वे और वैन डेर होवेन का एल्गोरिथम अभी भी सबसे अधिक होगा प्रभावी तरीकासंख्या गुणा करें।

कुछ त्वरित तरीके मौखिक गुणनहमने आपके साथ इसे पहले ही सुलझा लिया है, अब आइए इस पर करीब से नज़र डालें कि विभिन्न सहायक विधियों का उपयोग करके अपने दिमाग में संख्याओं को जल्दी से कैसे गुणा करें। आप पहले से ही जानते होंगे, और उनमें से कुछ काफी आकर्षक हैं, जैसे कि संख्याओं को गुणा करने का प्राचीन चीनी तरीका।

श्रेणी के अनुसार रैंकिंग

यह दो अंकों की संख्याओं को शीघ्रता से गुणा करने का सबसे सरल तरीका है। दोनों कारकों को दहाई और इकाई में विभाजित किया जाना चाहिए, और फिर इन सभी नई संख्याओं को एक दूसरे से गुणा किया जाना चाहिए।

इस पद्धति के लिए एक ही समय में अधिकतम चार संख्याओं को स्मृति में रखने और इन संख्याओं के साथ गणना करने की क्षमता की आवश्यकता होती है।

उदाहरण के लिए, आपको संख्याओं को गुणा करना होगा 38 तथा 56 . हम इसे इस तरह करते हैं:

38 * 56 = (30 + 8) * (50 + 6) = 30 * 50 + 8 * 50 + 30 * 6 + 8 * 6 = 1500 + 400 + 180 + 48 = 2128 तीन चरणों में दो अंकों की संख्याओं का मानसिक गुणा करना और भी आसान हो जाएगा। पहले आपको दहाई को गुणा करना है, फिर इकाई के दो गुणनफलों को दहाई से जोड़ना है, और फिर इकाई के गुणनफल को एक से जोड़ना है। यह इस तरह दिख रहा है: 38 * 56 = (30 + 8) * (50 + 6) = 30 * 50 + (8 * 50 + 30 * 6) + 8 * 6 = 1500 + 580 + 48 = 2128 इस पद्धति का सफलतापूर्वक उपयोग करने के लिए, आपको गुणन तालिका को अच्छी तरह से जानना होगा, दो-अंकीय और तीन-अंकीय संख्याओं को जल्दी से जोड़ने और गणितीय कार्यों के बीच स्विच करने में सक्षम होना चाहिए, मध्यवर्ती परिणामों को न भूलें। अंतिम कौशल मदद और विज़ुअलाइज़ेशन के साथ हासिल किया जाता है।

यह विधि सबसे तेज़ और सबसे कुशल नहीं है, इसलिए यह मौखिक गुणा के अन्य तरीकों की खोज करने लायक है।

नंबर फिटिंग

आप अंकगणितीय गणना को अधिक सुविधाजनक रूप में लाने का प्रयास कर सकते हैं। उदाहरण के लिए, संख्याओं का गुणनफल 35 तथा 49 इस तरह कल्पना की जा सकती है: 35 * 49 = (35 * 100) / 2 — 35 = 1715
यह विधि पिछले वाले की तुलना में अधिक प्रभावी हो सकती है, लेकिन यह सार्वभौमिक नहीं है और सभी मामलों के लिए उपयुक्त नहीं है। कार्य को सरल बनाने के लिए एक उपयुक्त एल्गोरिथम खोजना हमेशा संभव नहीं होता है।

इस विषय पर, मुझे एक किस्सा याद आया कि कैसे एक गणितज्ञ नदी के किनारे एक खेत के पास से गुजरा, और अपने वार्ताकारों से कहा कि वह जल्दी से कोरल में भेड़ों की संख्या, 1358 भेड़ों की गिनती करने में कामयाब रहा। जब उनसे पूछा गया कि उन्होंने यह कैसे किया, तो उन्होंने कहा कि सब कुछ सरल है - आपको पैरों की संख्या गिनने और 4 से विभाजित करने की आवश्यकता है।

एक कॉलम में गुणन का विज़ुअलाइज़ेशन

यह संख्याओं के मानसिक गुणन के सबसे बहुमुखी तरीकों में से एक है, जो स्थानिक कल्पना और स्मृति को विकसित करता है। सबसे पहले आपको अपने दिमाग में एक कॉलम में दो अंकों की संख्याओं को एक अंकों की संख्या से गुणा करना सीखना होगा। उसके बाद, आप दो अंकों की संख्याओं को तीन चरणों में आसानी से गुणा कर सकते हैं। सबसे पहले, दो अंकों की संख्या को दूसरी संख्या के दसियों से गुणा किया जाना चाहिए, फिर दूसरी संख्या की इकाइयों से गुणा किया जाना चाहिए, और फिर परिणामी संख्याओं का योग करना चाहिए।

यह इस तरह दिख रहा है: 38 * 56 = (38 * 5) * 10 + 38 * 6 = 1900 + 228 = 2128

संख्याओं की व्यवस्था के साथ विज़ुअलाइज़ेशन

दो अंकों की संख्याओं को गुणा करने का एक बहुत ही रोचक तरीका इस प्रकार है। सैकड़ों, इकाई और दहाई प्राप्त करने के लिए संख्याओं को क्रमिक रूप से गुणा करना आवश्यक है।

मान लीजिए कि आप गुणा करना चाहते हैं 35 पर 49 .

पहले गुणा करें 3 पर 4 , आपको मिला 12 , फिर 5 तथा 9 , आपको मिला 45 . लिखो 12 तथा 5 , उनके बीच एक जगह के साथ, और 4 याद करना।

आपको मिला: 12 __ 5 (याद करना 4 ).

अब गुणा करें 3 पर 9 , तथा 5 पर 4 , और योग करें: 3 * 9 + 5 * 4 = 27 + 20 = 47 .

अब आपको चाहिए 47 जोड़ें 4 जो हमें याद है। हम पाते हैं 51 .

हम लिखते हैं 1 बीच में और 5 इसमें जोड़ें 12 , हम पाते हैं 17 .

तो, हम जिस नंबर की तलाश कर रहे थे 1715 , यह उत्तर है:

35 * 49 = 1715
इसी तरह मानसिक रूप से गुणा करने का प्रयास करें: 18 * 34, 45 * 91, 31 * 52 .

चीनी या जापानी गुणन

एशियाई देशों में, संख्याओं को एक कॉलम में नहीं, बल्कि रेखाएँ खींचकर गुणा करने की प्रथा है। पूर्वी संस्कृतियों के लिए, चिंतन और दृश्य की इच्छा महत्वपूर्ण है, शायद यही वजह है कि वे इतनी सुंदर विधि लेकर आए हैं जो आपको किसी भी संख्या को गुणा करने की अनुमति देती है। यह विधि पहली नज़र में ही जटिल है। वास्तव में, अधिक दृश्यता आपको कॉलम में गुणा की तुलना में इस पद्धति का अधिक कुशलता से उपयोग करने की अनुमति देती है।

साथ ही इस प्राचीन प्राच्य पद्धति का ज्ञान आपके विद्वता को बढ़ाता है। सहमत हूं, हर कोई उस प्राचीन गुणन प्रणाली को जानने का दावा नहीं कर सकता है जिसका इस्तेमाल चीनियों ने 3000 साल पहले किया था।

चीनी कैसे संख्याओं को गुणा करते हैं इस पर वीडियो

आप "सभी पाठ्यक्रम" और "उपयोगिता" अनुभागों में अधिक विस्तृत जानकारी प्राप्त कर सकते हैं, जिसे साइट के शीर्ष मेनू के माध्यम से एक्सेस किया जा सकता है। इन अनुभागों में, लेखों को विभिन्न विषयों पर सबसे विस्तृत (जहाँ तक संभव हो) जानकारी वाले ब्लॉकों में विषय के आधार पर समूहीकृत किया जाता है।

आप ब्लॉग की सदस्यता भी ले सकते हैं, और सभी नए लेखों के बारे में जान सकते हैं।
इसमें ज्यादा समय नहीं लगता है। बस नीचे दिए गए लिंक पर क्लिक करें:

शैक्षणिक विज्ञान के उम्मीदवार नतालिया करपुशिना।

बहु-अंकीय संख्याओं के गुणन में महारत हासिल करने के लिए, आपको केवल गुणन तालिका जानने और संख्याओं को जोड़ने में सक्षम होने की आवश्यकता है। संक्षेप में, पूरी कठिनाई इस बात में निहित है कि गुणन (आंशिक उत्पादों) के मध्यवर्ती परिणामों को सही ढंग से कैसे रखा जाए। गणना को आसान बनाने के प्रयास में, लोग संख्याओं को गुणा करने के कई तरीके लेकर आए हैं। गणित के सदियों पुराने इतिहास में, उनमें से कई दर्जन हैं।

जाली विधि से गुणा। अंकगणित पर पहली मुद्रित पुस्तक से चित्रण। 1487.

नेपियर की छड़ें। इस सरल काउंटिंग डिवाइस का वर्णन सबसे पहले जॉन नेपियर की कृति "रैबडोलोजी" में किया गया था। 1617.

जॉन नेपियर (1550-1617)।

स्किकर्ड की गणना मशीन मॉडल। यह कंप्यूटिंग डिवाइस, जो हमारे पास नहीं आया है, आविष्कारक द्वारा 1623 में बनाया गया था और उसके द्वारा एक साल बाद जोहान्स केप्लर को एक पत्र में वर्णित किया गया था।

विल्हेम शिकार्ड (1592-1635)।

हिंदू विरासत - झंझरी का एक तरीका

हिंदू, जो प्राचीन काल से दशमलव संख्या प्रणाली को जानते हैं, लिखित खाते के बजाय मौखिक खाते को प्राथमिकता देते थे। उन्होंने तेजी से गुणा करने के कई तरीके ईजाद किए। बाद में, उन्हें अरबों द्वारा उधार लिया गया, और उनसे ये तरीके यूरोपीय लोगों के पास चले गए। हालाँकि, उन्होंने खुद को उन तक सीमित नहीं रखा और नए विकसित किए, विशेष रूप से, जो स्कूल में पढ़ाया जाता है - एक कॉलम द्वारा गुणा। इस पद्धति को 15वीं शताब्दी की शुरुआत से जाना जाता है, अगली शताब्दी में यह गणितज्ञों के बीच मजबूती से स्थापित हो गई और आज इसका उपयोग हर जगह किया जाता है। लेकिन क्या इस अंकगणितीय ऑपरेशन को करने के लिए कॉलम से गुणा करना सबसे अच्छा तरीका है? वास्तव में, हमारे समय में गुणा के अन्य, भूले हुए तरीके हैं, इससे भी बदतर, उदाहरण के लिए, जाली विधि।

इस पद्धति का उपयोग पुरातनता में किया गया था, मध्य युग में यह पूर्व में व्यापक रूप से फैल गया था, और पुनर्जागरण में - यूरोप में। जाली विधि को भारतीय, मुस्लिम या "कोशिका में गुणन" भी कहा जाता था। और इटली में इसे "जेलोसिया", या "जाली गुणन" (इतालवी से अनुवादित गेलोसिया - "अंधा", "जाली शटर") कहा जाता था। दरअसल, संख्याओं के गुणन से प्राप्त आंकड़े शटर-ब्लाइंड से मिलते-जुलते थे, जो सूरज से वेनिस के घरों की खिड़कियां बंद कर देते थे।

हम एक उदाहरण के साथ इस सरल गुणन विधि के सार की व्याख्या करेंगे: हम उत्पाद 296 × 73 की गणना करेंगे। आइए वर्ग कोशिकाओं के साथ एक तालिका बनाकर शुरू करें, जिसमें अंकों की संख्या से तीन कॉलम और दो पंक्तियाँ होंगी। गुणक। कोशिकाओं को आधा तिरछे में विभाजित करें। हम तालिका के ऊपर संख्या 296 लिखते हैं, और संख्या 73 लंबवत दाईं ओर। हम पहली संख्या के प्रत्येक अंक को दूसरे के प्रत्येक अंक से गुणा करते हैं और उत्पादों को संबंधित कोशिकाओं में लिखते हैं, दसियों को विकर्ण से ऊपर रखते हैं, और इकाइयाँ इसके नीचे। तिरछी धारियों में संख्याओं को जोड़कर वांछित उत्पाद की संख्याएँ प्राप्त की जाती हैं। इस मामले में, हम निचले दाएं सेल से शुरू होकर दक्षिणावर्त घूमेंगे: 8, 2 + 1 + 7, आदि। हम परिणाम तालिका के नीचे और साथ ही इसके बाईं ओर लिखते हैं। (यदि जोड़ दो अंकों का योग बनता है, तो हम केवल इकाइयों को इंगित करते हैं, और दहाई को अगली पट्टी से अंकों के योग में जोड़ते हैं।) उत्तर: 21,608। तो, 296 x 73 = 21,608।

जाली विधि किसी भी तरह से स्तंभ गुणन से कमतर नहीं है। यह और भी सरल और अधिक विश्वसनीय है, इस तथ्य के बावजूद कि दोनों मामलों में किए गए कार्यों की संख्या समान है। सबसे पहले, आपको केवल सिंगल-डिजिट और डबल-डिजिट नंबरों के साथ काम करना है, और वे दिमाग में काम करना आसान है। दूसरे, मध्यवर्ती परिणामों को याद रखने और उन्हें लिखने के क्रम पर नज़र रखने की कोई आवश्यकता नहीं है। मेमोरी अनलोड हो जाती है, और ध्यान संरक्षित रहता है, इसलिए त्रुटि की संभावना कम हो जाती है। इसके अलावा, जाली विधि आपको जल्दी से परिणाम प्राप्त करने की अनुमति देती है। इसमें महारत हासिल करने के बाद, आप अपने लिए देख सकते हैं।

जाली विधि सही उत्तर की ओर क्यों ले जाती है? इसका "तंत्र" क्या है? आइए पहले के समान निर्मित तालिका का उपयोग करके इसे समझें, केवल इस मामले में कारकों को 200 + 90 + 6 और 70 + 3 के योग के रूप में प्रस्तुत किया जाता है।

जैसा कि आप देख सकते हैं, पहली तिरछी पट्टी में इकाइयाँ हैं, दूसरी में दहाई, तीसरी में सैकड़ों, और इसी तरह। जब जोड़ा जाता है, तो वे उत्तर में क्रमशः इकाइयों की संख्या, दहाई, सैकड़ा आदि देते हैं। निम्नलिखित क्या स्पष्ट है:

दूसरे शब्दों में, अंकगणित के नियमों के अनुसार, संख्या 296 और 73 के गुणनफल की गणना निम्नानुसार की जाती है:

296 x 73 = (200 + 90 + 6) x (70 + 3) = 14000 + 6300 + 420 + 600 + 270 + 18 = 10000 + (4000 + 6000) + (300 + 400 + 600 + 200) + (70) + 20 + 10) + 8 = 21,608।

नेपियर की छड़ें

जाली विधि द्वारा गुणा एक सरल और मूल गणना उपकरण - नेपियर की छड़ें का आधार है। इसके आविष्कारक, जॉन नेपियर, एक स्कॉटिश बैरन और गणित के प्रेमी, पेशेवरों के साथ, गणना के साधनों और विधियों में सुधार करने में लगे हुए थे। विज्ञान के इतिहास में, उन्हें मुख्य रूप से लघुगणक के रचनाकारों में से एक के रूप में जाना जाता है।

डिवाइस में दस शासक होते हैं, जिस पर गुणन तालिका रखी जाती है। विकर्ण द्वारा अलग किए गए प्रत्येक सेल में, 1 से 9 तक दो एकल-अंकीय संख्याओं का गुणनफल लिखा जाता है: ऊपरी भाग में दहाई की संख्या इंगित की जाती है, निचले भाग में लोगों की संख्या इंगित की जाती है। एक शासक (बाएं) तय किया गया है, बाकी को वांछित संख्यात्मक संयोजन के साथ एक स्थान से दूसरे स्थान पर पुनर्व्यवस्थित किया जा सकता है। नेपियर की छड़ियों का उपयोग करके, बहु-अंकीय संख्याओं को गुणा करना आसान है, इस ऑपरेशन को जोड़ में कम करना।

उदाहरण के लिए, संख्याओं 296 और 73 के गुणनफल की गणना करने के लिए, आपको 296 को 3 से और 70 से (पहले 7, फिर 10 से) गुणा करना होगा और परिणामी संख्याओं को जोड़ना होगा। हम तीन अन्य को निश्चित शासक से जोड़ देंगे - शीर्ष पर संख्या 2, 9 और 6 के साथ (उन्हें संख्या 296 बनानी चाहिए)। अब आइए तीसरी पंक्ति को देखें (पंक्ति संख्याएं चरम रूलर पर दर्शाई गई हैं)। इसमें संख्याएँ हमारे लिए पहले से परिचित एक सेट बनाती हैं।

उन्हें जोड़ने पर, जाली विधि की तरह, हमें 296 x 3 = 888 मिलता है। इसी तरह, सातवीं पंक्ति पर विचार करते हुए, हम पाते हैं कि 296 x 7 = 2072, फिर 296 x 70 = 20,720। इस प्रकार,
296 x 73 = 20,720 + 888 = 21,608।

नेपियर की छड़ियों का उपयोग अधिक जटिल कार्यों - विभाजन और वर्गमूल निष्कर्षण के लिए भी किया जाता था। इस गिनती उपकरण ने बार-बार सुधार करने और इसे काम में अधिक सुविधाजनक और कुशल बनाने की कोशिश की है। दरअसल, कई मामलों में, संख्याओं को गुणा करने के लिए, उदाहरण के लिए, दोहराई जाने वाली संख्याओं के साथ, कई सेटों की आवश्यकता होती है। लेकिन इस तरह की समस्या को शासकों को घूर्णन सिलेंडरों के साथ प्रतिस्थापित करके उनमें से प्रत्येक की सतह पर लागू गुणन तालिका के साथ उसी रूप में हल किया गया था जैसा नेपियर ने इसे प्रस्तुत किया था। लाठी के एक सेट के बजाय, नौ एक बार में प्राप्त किए गए थे।

इस तरह की तरकीबों ने वास्तव में गणना में तेजी लाई और सुविधा प्रदान की, लेकिन नेपियर डिवाइस के संचालन के मुख्य सिद्धांत को प्रभावित नहीं किया। तो जाली विधि ने दूसरा जीवन प्राप्त किया, जो कई और शताब्दियों तक चला।

शिकारार्ड मशीन

वैज्ञानिकों ने लंबे समय से इस बारे में सोचा है कि कठिन कम्प्यूटेशनल कार्य को यांत्रिक उपकरणों में कैसे स्थानांतरित किया जाए। गणना मशीनों के निर्माण में पहला सफल कदम 17वीं शताब्दी में ही बना था। ऐसा माना जाता है कि जर्मन गणितज्ञ और खगोलशास्त्री विल्हेम शिकार्ड ने दूसरों की तुलना में पहले भी इसी तरह का तंत्र बनाया था। लेकिन, विडंबना यह है कि केवल लोगों के एक संकीर्ण दायरे को ही इसके बारे में पता था, और इस तरह के एक उपयोगी आविष्कार को दुनिया को 300 से अधिक वर्षों तक नहीं पता था। इसलिए, इसने कंप्यूटिंग सुविधाओं के बाद के विकास को प्रभावित नहीं किया। जोहान्स केपलर के अभिलेखागार में केवल आधी सदी पहले शिकार्ड मशीन का विवरण और रेखाचित्र खोजा गया था, और थोड़ी देर बाद, जीवित दस्तावेजों के अनुसार, इसका कामकाजी मॉडल बनाया गया था।

संक्षेप में, स्किकर्ड मशीन छह अंकों का यांत्रिक कैलकुलेटर है जो संख्याओं का जोड़, घटाव, गुणा और भाग करता है। इसके तीन भाग होते हैं: एक गुणा करने वाला उपकरण, एक जोड़ने वाला उपकरण और मध्यवर्ती परिणामों को संग्रहीत करने के लिए एक तंत्र। पहले का आधार था, जैसा कि आप अनुमान लगा सकते हैं, नेपियर की छड़ें, सिलेंडरों में लुढ़क गईं। वे छह . से जुड़े थे ऊर्ध्वाधर कुल्हाड़ियोंऔर मशीन के शीर्ष पर स्थित विशेष हैंडल की मदद से मुड़ गया। सिलेंडरों के सामने खिड़कियों की नौ पंक्तियों वाला एक पैनल था, प्रत्येक में छह, जो आवश्यक संख्याओं को देखने और बाकी को छिपाने के लिए आवश्यक होने पर साइड कुंडी के साथ खोले और बंद किए गए थे।

शिकारर्ड काउंटिंग मशीन ऑपरेशन में बहुत सरल है। यह पता लगाने के लिए कि 296 x 73 का गुणनफल क्या है, आपको सिलेंडरों को उस स्थिति में सेट करने की आवश्यकता है जिसमें पहला गुणक खिड़कियों की ऊपरी पंक्ति में दिखाई देता है: 000296। हमें 296 x 3 का गुणनफल प्राप्त होता है। तीसरी पंक्ति और देखी गई संख्याओं का योग, जैसा कि जाली विधि में है। इसी प्रकार सातवीं पंक्ति की खिड़कियाँ खोलने पर हमें गुणनफल 296 x 7 प्राप्त होता है, जिसमें हम दायीं ओर 0 जोड़ते हैं। यह केवल योजक पर मिलने वाली संख्याओं को जोड़ने के लिए रहता है।

एक बार भारतीयों द्वारा आविष्कार किया गया, बहु-अंकीय संख्याओं को गुणा करने का एक तेज़ और विश्वसनीय तरीका, जिसका उपयोग कई सदियों से गणना में किया जाता है, अब, अफसोस, भुला दिया गया है। लेकिन वह आज भी हमारी मदद कर सकते थे, अगर कैलकुलेटर इतना परिचित न होता।