फाइबोनैचि संख्याएँ.

कई संयुक्त समस्याओं को हल करते समय, वे किसी दी गई समस्या को कम संख्या में तत्वों वाली समस्या में बदलने की विधि का उपयोग करते हैं। उदाहरण के लिए, आप क्रमपरिवर्तन की संख्या के लिए एक सूत्र प्राप्त कर सकते हैं:

इससे पता चलता है कि इसे हमेशा छोटी संख्या के भाज्य में घटाया जा सकता है।

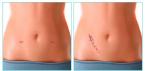
पुनरावृत्ति संबंधों के निर्माण का एक अच्छा उदाहरण फाइबोनैचि समस्या है। 1202 में अपनी पुस्तक में, इतालवी गणितज्ञ फिबोनाची ने निम्नलिखित समस्या प्रस्तुत की। खरगोशों का एक जोड़ा महीने में एक बार दो युवा खरगोशों (एक मादा और एक नर) को जन्म देता है, और नवजात खरगोश जन्म के दो महीने बाद स्वयं संतान पैदा करते हैं। यदि शुरुआत में खरगोशों का एक जोड़ा था तो एक वर्ष में कितने खरगोश पैदा होंगे?

समस्या की स्थितियों से यह पता चलता है कि एक महीने में खरगोशों के दो जोड़े होंगे, दो महीने में केवल खरगोशों की पहली जोड़ी जो दो महीने पहले दिखाई दी थी, संतान पैदा करेगी, इसलिए कुल मिलाकर 3 जोड़े खरगोश होंगे। एक और महीने में पहले से ही 5 जोड़े होंगे। और इसी तरह।

आइए हम वर्ष की शुरुआत से महीनों के बाद खरगोशों के जोड़े की संख्या से निरूपित करें। फिर एक महीने के बाद सूत्र का उपयोग करके खरगोशों के जोड़े की संख्या ज्ञात की जा सकती है:

इस निर्भरता को कहा जाता है पुनरावृत्ति संबंध . शब्द "रिकर्सन" का अर्थ है पीछे जाना (हमारे मामले में, पिछले परिणामों पर वापस जाना)।

शर्त के अनुसार, और, फिर संबंध के अनुसार हमारे पास:,,, आदि हैं।

परिभाषा 1:नंबरों को बुलाया जाता है फाइबोनैचि संख्याएँ . यह गणित में संख्याओं का एक प्रसिद्ध क्रम है:

1, 1, 2, 3, 5, 8, 13, 21, ...

इस क्रम में, प्रत्येक अगली संख्या पिछली दो संख्याओं का योग होती है। तथा पुनरावृत्ति संबंध में अगला पद भी पिछले दो पदों के योग के रूप में पाया जाता है।

आइए हम फाइबोनैचि संख्याओं और संयोजन समस्या के बीच संबंध स्थापित करें। मान लीजिए कि हमें शून्य और एक से मिलकर ऐसे कई अनुक्रम खोजने की ज़रूरत है जिनमें कोई भी दो एक पंक्ति में न हों।

आइए ऐसे किसी भी क्रम को लें और निम्नलिखित नियम के अनुसार खरगोशों की एक जोड़ी का मिलान करें: एक इस जोड़ी के "पूर्वजों" (मूल एक सहित) के जोड़े में से एक के जन्म के महीनों के अनुरूप है, और शून्य अन्य सभी के अनुरूप है महीने. उदाहरण के लिए, अनुक्रम ऐसी "वंशावली" स्थापित करता है - जोड़ा स्वयं 11वें महीने के अंत में प्रकट हुआ, उसके माता-पिता 7वें महीने के अंत में, "दादा" 5वें महीने के अंत में, और "महान" -दादाजी” दूसरे महीने के अंत में। प्रारंभिक जोड़ी अनुक्रम के साथ एन्क्रिप्टेड है। किसी भी क्रम में दो इकाइयाँ एक पंक्ति में खड़ी नहीं हो सकतीं - एक जोड़ा जो अभी-अभी सामने आया है वह एक महीने में संतान उत्पन्न नहीं कर सकता है। जाहिर है, अलग-अलग अनुक्रम अलग-अलग जोड़ियों के अनुरूप होते हैं और इसके विपरीत भी।

इस प्रकार, निर्दिष्ट गुणों वाले अनुक्रमों की संख्या बराबर है।

प्रमेय 1:संख्या द्विपद गुणांकों के योग के रूप में पाई जाती है:. यदि - विषम, तो . यदि – सम, तो . अन्यथा:- संख्या का पूर्णांक भाग।

सबूत:दरअसल, 0 और 1 के सभी अनुक्रमों की संख्या है जिसमें कोई भी दो 1 आसन्न नहीं हैं। बिल्कुल एक और शून्य वाले ऐसे अनुक्रमों की संख्या बराबर होती है, और फिर 0 से भिन्न होती है। योग नियम लागू करने पर हमें यह योग प्राप्त होता है।

इस समानता को अलग ढंग से सिद्ध किया जा सकता है। आइए निरूपित करें:

समानता से यह निष्कर्ष निकलता है कि . इसके अतिरिक्त यह भी स्पष्ट है कि. चूंकि दोनों अनुक्रम और पुनरावृत्ति संबंध को संतुष्ट करते हैं, तो, और।

परिभाषा 2:पुनरावृत्ति संबंध है आदेश , यदि यह अनुक्रम के पिछले सदस्यों के माध्यम से गणना की अनुमति देता है: .

उदाहरण के लिए, दूसरे क्रम का पुनरावृत्ति संबंध है, और तीसरे क्रम का पुनरावृत्ति संबंध है। फाइबोनैचि अनुपात एक दूसरे क्रम का संबंध है।

परिभाषा 3: समाधान द्वारापुनरावृत्ति संबंध एक अनुक्रम है जो इस संबंध को संतुष्ट करता है।

यदि क्रम का पुनरावृत्ति संबंध दिया गया है, तो यह अनंत अनुक्रमों से संतुष्ट होता है, क्योंकि पहले तत्वों को मनमाने ढंग से सेट किया जा सकता है। लेकिन यदि पहले तत्व दिए गए हैं, तो शेष पद विशिष्ट रूप से निर्धारित किए जाते हैं।

उदाहरण के लिए, ऊपर चर्चा किए गए अनुक्रम 1, 1, 2, 3, 5, 8, 13, 21, ... के अलावा, फाइबोनैचि अनुपात को अन्य अनुक्रमों से भी संतुष्ट किया जा सकता है। उदाहरण के लिए, अनुक्रम 2, 2, 4, 8, 12,... एक ही सिद्धांत के अनुसार बनाया गया है। लेकिन यदि आप प्रारंभिक शब्द निर्दिष्ट करते हैं (फाइबोनैचि अनुक्रम में उनमें से 2 हैं), तो समाधान विशिष्ट रूप से निर्धारित होता है। रिश्ते के क्रम के रूप में कई प्रारंभिक शर्तों को लिया जाता है।

ज्ञात पुनरावृत्ति संबंधों और प्रारंभिक शब्दों का उपयोग करके, हम अनुक्रम के पदों को एक के बाद एक लिख सकते हैं और इस तरह हम इसके किसी भी पद को प्राप्त कर सकते हैं। लेकिन कई मामलों में, हमें पिछले सभी सदस्यों की नहीं, बल्कि केवल एक विशिष्ट सदस्य की आवश्यकता होती है। इस मामले में, अनुक्रम के वें पद के लिए एक सूत्र रखना अधिक सुविधाजनक है।

हम कहेंगे कि एक निश्चित अनुक्रम किसी दिए गए पुनरावृत्ति संबंध का एक समाधान है यदि, इस अनुक्रम के प्रतिस्थापन पर, संबंध समान रूप से संतुष्ट होता है।

उदाहरण के लिए, अनुक्रम संबंध के समाधानों में से एक है:। एक साधारण प्रतिस्थापन से इसे जांचना आसान है।

परिभाषा 4:-वें क्रम के पुनरावृत्ति संबंध का समाधान कहा जाता है सामान्य , यदि यह मनमाने स्थिरांक पर निर्भर करता है, जिसे बदलकर, कोई इस संबंध का कोई भी समाधान प्राप्त कर सकता है।

उदाहरण के लिए, संबंध के लिए सामान्य समाधान होगा।

दरअसल, यह सत्यापित करना आसान है कि यह हमारे रिश्ते का समाधान होगा। आइए हम दिखाएं कि कोई भी समाधान इस रूप में प्राप्त किया जा सकता है। उन्हें मनमानी करने दीजिए.

फिर वो लोग होंगे जो

जाहिर है, किसी भी समीकरण प्रणाली का एक अनूठा समाधान होता है।

परिभाषा 5:पुनरावृत्ति संबंध कहलाता है रेखीय , यदि यह फॉर्म में लिखा गया है:

संख्यात्मक गुणांक कहाँ हैं.

सामान्यतया, मनमाने ढंग से आवर्ती संबंधों को हल करने के लिए कोई सामान्य नियम नहीं हैं। हालाँकि, रैखिक पुनरावृत्ति संबंधों को हल करने के लिए वहाँ है सामान्य नियमसमाधान।

आइए पहले दूसरे क्रम के संबंध पर विचार करें।

इस रिश्ते का समाधान निम्नलिखित कथनों पर आधारित है।

प्रमेय 2:यदि और - दूसरे क्रम के दिए गए पुनरावृत्ति संबंध का एक समाधान है, तो किसी भी संख्या और अनुक्रम के लिए भी इस संबंध का एक समाधान है।

प्रमेय 3:यदि संख्या द्विघात समीकरण का मूल है, तो अनुक्रम पुनरावृत्ति संबंध का समाधान है।

प्रमेयों से 2, 3 दूसरे क्रम के रैखिक पुनरावृत्ति संबंधों को हल करने के लिए निम्नलिखित नियम का पालन किया जाता है।

एक पुनरावृत्ति संबंध दिया जाए.

1) आइए एक द्विघात समीकरण बनाते हैं, जिसे कहा जाता है विशेषता किसी दिए गए अनुपात के लिए. पता लगाते हैं सभीइस समीकरण की जड़ें (यहां तक ​​कि एकाधिक और जटिल)।

2) आइए पुनरावृत्ति संबंध का एक सामान्य समाधान बनाएं। इसकी संरचना जड़ों के प्रकार पर निर्भर करती है (वे समान या भिन्न होती हैं)।

a) यदि इस संबंध में दो हैं विभिन्न जड़ेंऔर, तब संबंध के सामान्य समाधान का रूप होता है।

दरअसल, प्रमेयों से 2, 3 यह इस प्रकार है - समाधान और समीकरणों की प्रणाली

इसका एक ही समाधान है, क्योंकि मान लें कि ।

उदाहरण के लिए, फाइबोनैचि संख्याओं के लिए, हमारे पास है। विशेषता समीकरण का रूप है: . अंतिम समीकरण को हल करने पर, हमें मूल प्राप्त होते हैं:,।

यदि विशेषता समीकरण की सभी जड़ें अलग-अलग हैं, तो सामान्य समाधान का रूप है: .

यदि, उदाहरण के लिए, तो यह रूट समाधान से मेल खाता है:

इस पुनरावृत्ति संबंध का. सामान्य समाधान में, यह मूल भाग से मेल खाता है।

उदाहरण के लिए, पुनरावृत्ति संबंध को हल करना:

हम फॉर्म का एक विशिष्ट समीकरण बनाते हैं:।

इसकी जड़ें हैं... इसलिए, एक सामान्य समाधान है.

बड़ी मात्रा में अवलोकन डेटा के साथ एक्ससंभावना समीकरण को हल करने की सीमित विधियाँ बड़ी संख्या में प्रारंभिक डेटा और गणना के मध्यवर्ती परिणामों को याद रखने की आवश्यकता से जुड़ी महत्वपूर्ण कम्प्यूटेशनल कठिनाइयों को जन्म देती हैं। इस संबंध में, विशेष रुचि आवर्ती तरीकों की है जिसमें अधिकतम संभावना अनुमान की गणना धीरे-धीरे बढ़ती सटीकता के साथ चरणों में की जाती है, प्रत्येक चरण नए अवलोकन डेटा प्राप्त करने से जुड़ा होता है, और आवर्ती प्रक्रिया का निर्माण इस तरह से किया जाता है कि इसे स्मृति में संग्रहीत किया जा सके। पिछले चरणों से डेटा की न्यूनतम संभव मात्रा। व्यावहारिक दृष्टिकोण से आवर्ती तरीकों का एक अतिरिक्त और बहुत महत्वपूर्ण लाभ किसी भी मध्यवर्ती चरण पर परिणाम देने की उनकी तत्परता है।

यह उन मामलों में भी आवर्ती तरीकों का उपयोग करने की सलाह देता है जहां परिमित विधि द्वारा अधिकतम संभावना समीकरण का सटीक समाधान प्राप्त करना संभव है, और जब अधिकतम का अनुमान लगाने के लिए सटीक विश्लेषणात्मक अभिव्यक्ति ढूंढना असंभव होता है तो उन्हें और भी अधिक मूल्यवान बनाता है। संभावना.

मान लीजिए कि अवलोकन डेटा का सेट एक अनुक्रम है जिसका वर्णन करने के लिए हम एक वेक्टर का परिचय देते हैं। (हमेशा की तरह, इसका प्रत्येक घटक, बदले में, एक वेक्टर, एक यादृच्छिक प्रक्रिया का एक खंड, आदि हो सकता है)। चलो संभावना समारोह हो, और

इसका लघुगणक. उत्तरार्द्ध को हमेशा फॉर्म में दर्शाया जा सकता है

अंतिम मान के बिना अवलोकन डेटा की आबादी के लिए संभावना फ़ंक्शन का लघुगणक, और

और के दिए गए मानों के लिए मान की सशर्त संभाव्यता घनत्व का लघुगणक।

संभावना फ़ंक्शन के लघुगणक के लिए प्रतिनिधित्व (7.5.16) अधिकतम संभावना अनुमान की गणना के लिए आवर्ती प्रक्रिया प्राप्त करने का आधार है। आइए नियमित मामले पर विचार करें। इस मामले में, अधिकतम संभावना अनुमान को समीकरण के समाधान के रूप में पाया जा सकता है

जो केवल सूचकांक प्रस्तुत करने से (7.1.6) से भिन्न है पी वाईसंभाव्यता फ़ंक्शन का लघुगणक।

आइए हम इस समीकरण के समाधान को इस बात पर जोर देकर निरूपित करें कि यह अनुमान अवलोकन डेटा के एक सेट से प्राप्त किया गया था। इसी प्रकार, आइए समीकरण के समाधान द्वारा डेटा की समग्रता से प्राप्त अधिकतम संभावना अनुमान को निरूपित करें।

समीकरण (7.5.19) को निम्नलिखित रूप में (7.5.16) को ध्यान में रखते हुए फिर से लिखा जा सकता है:

आइए हम बिंदु के पड़ोस में टेलर श्रृंखला में (7.5.20) के बाईं ओर का विस्तार करें। जिसमें

(7.5.22)

बिंदु पर फ़ंक्शन का ग्रेडिएंट वेक्टर; यह पद इस तथ्य के कारण शून्य हो जाता है कि, पिछले के लिए संभाव्यता समीकरण का एक समाधान है (पी -पहला चरण:

बिंदु पर संभावना फ़ंक्शन के लघुगणक के दूसरे व्युत्पन्न का एक सममित मैट्रिक्स, विपरीत चिह्न के साथ लिया गया, विस्तार के अलिखित शब्दों में अंतर के संबंध में छोटेपन का एक द्विघात और उच्च क्रम होता है। इन उत्तरार्द्धों की उपेक्षा करते हुए, हमें अधिकतम संभावना समीकरण का निम्नलिखित अनुमानित समाधान प्राप्त होता है:

व्युत्क्रम मैट्रिक्स कहां है.

यह समाधान एक पुनरावृत्ति संबंध के रूप में प्रस्तुत किया गया है जो पिछले चरण के अनुमान और सुधार के माध्यम से अनुमान का अगला मूल्य निर्धारित करता है , सीधे और पिछले मूल्यांकन के माध्यम से उपलब्ध अवलोकन डेटा पर निर्भर करता है। सुधार नए प्राप्त मूल्य की सशर्त संभाव्यता घनत्व के लघुगणक के ढाल के उत्पाद के रूप में बनता है एक्स n पिछले अनुमान के बराबर एक बिंदु पर, भार मैट्रिक्स के लिए . उत्तरार्द्ध अभिव्यक्ति (7.5.23) द्वारा निर्धारित किया जाता है और पिछले चरण के अनुमान पर भी निर्भर करता है, और नए अवलोकन डेटा पर इसकी निर्भरता पूरी तरह से सशर्त संभाव्यता घनत्व के लघुगणक के रूप से निर्धारित होती है।

संबंध का रूप (7.5.24) (7.5.8) के समान है, जो न्यूटन की विधि का उपयोग करके अधिकतम संभावना अनुमान की गणना करने की एक पुनरावृत्त विधि लागू करता है। हालाँकि, वास्तव में वे एक-दूसरे से काफी भिन्न हैं। (7.5.8) में, पिछले अनुमान मूल्य में सुधार संपूर्ण संभावना फ़ंक्शन के लघुगणक के ग्रेडिएंट द्वारा निर्धारित किया जाता है, जो हमेशा सभी उपलब्ध अवलोकन डेटा पर निर्भर करता है, जिसके लिए इस पूरे सेट को याद रखने की आवश्यकता होती है। (7.5.24) के अनुसार, सुधार ग्रेडिएंट के परिमाण द्वारा निर्धारित किया जाता है, जो सशर्त संभाव्यता घनत्व के गुणों के कारण, वास्तव में केवल उन मूल्यों () पर निर्भर करता है जो एक मजबूत सांख्यिकीय कनेक्शन में हैं साथ एक्सएन। यह अंतर एक मान से कम किए गए अवलोकन डेटा के एक सेट से पाए गए अधिकतम संभावना अनुमान के रूप में पिछले सन्निकटन की विशेष पसंद का परिणाम है, और विशेष रूप से () के स्वतंत्र मूल्यों के लिए उच्चारित किया जाता है। इस आखिरी मामले में

जिसके कारण यह केवल और पर निर्भर करता है एक्स n , और ग्रेडिएंट केवल अनुमान के पिछले मूल्य और नए प्राप्त मूल्य से है पी-अवलोकन डेटा का mstep। इसलिए, स्वतंत्र मूल्यों के साथ, एक वेक्टर बनाने के लिए, मूल्यांकन मूल्य को छोड़कर पिछले चरण से किसी भी अन्य जानकारी को याद रखना आवश्यक नहीं है।

इसी तरह, अवलोकन डेटा के मार्कोव अनुक्रम के मामले में, यानी, जब

वेक्टर केवल वर्तमान और एक पिछले मान पर निर्भर करता है। इस मामले में, गणना के लिए, पिछले चरण से, मूल्य के अलावा, केवल मूल्य को याद रखना आवश्यक है, लेकिन अवलोकन डेटा के पूरे सेट को नहीं, जैसा कि पुनरावृत्तीय प्रक्रिया में होता है। सामान्य तौर पर, गणना के लिए बड़ी संख्या में पिछले मानों को संग्रहीत करने की आवश्यकता हो सकती है (), हालांकि, केवल उन मानों को ध्यान में रखने की आवश्यकता के कारण जो सांख्यिकीय रूप से निर्भर हैं, यह संख्या लगभग हमेशा कुल मात्रा से कम होती है अवलोकन डेटा का. इस प्रकार, यदि कोई वेक्टर किसी समय अनुक्रम का वर्णन करता है, तो इस अनुक्रम के याद किए जाने वाले सदस्यों की संख्या उसके सहसंबंध समय से निर्धारित होती है, और उनका सापेक्ष अनुपात व्युत्क्रम अनुपात में घट जाता है एन, जैसा कि स्वतंत्र मूल्यों के मामले में होता है।

आइए अब पुनरावृत्ति संबंध (7.5.24) में शामिल भार मैट्रिक्स की संरचना पर विचार करें। परिभाषा (7.5.23) के अनुसार, एक पद की उपस्थिति के कारण, यह, सामान्यतया, स्वतंत्र मूल्यों के साथ भी सभी मूल्यों पर निर्भर करता है, जो पुनरावृत्ति संबंध (7.5.24) के लाभों से वंचित करता है पिछले चरण से संग्रहीत डेटा की मात्रा में संभावित कमी से जुड़ा हुआ है। मैट्रिक्स गणना का अनुमान लगाने के कई तरीके हैं , जो इस कमी को दूर करता है.

उनमें से पहला अनुमान और के दो अगले मूल्यों के बीच एक छोटे अंतर की बुनियादी धारणा के अधिक सुसंगत उपयोग पर आधारित है, जो पुनरावृत्ति संबंध (7.5.24) प्राप्त करने का आधार है। यह हमें वजन मैट्रिक्स के लिए एक समान पुनरावृत्ति संबंध प्राप्त करने की अनुमति देता है। वास्तव में, (7.5.23) से लघुता का उपयोग करते हुए, हमारे पास है

पदनाम दर्ज करके

(7.5.24) और (7.5.25) से हम वेक्टर और भार मैट्रिक्स के लिए आवर्ती संबंधों की एक प्रणाली प्राप्त करते हैं

यह प्रणाली, प्रारंभिक मूल्यों के साथ, किसी भी चरण में अनुमान के मूल्य को पूरी तरह से निर्धारित करती है, उनमें से प्रत्येक पर वर्तमान देखे गए मूल्य के लिए सशर्त संभाव्यता घनत्व के लघुगणक के दूसरे डेरिवेटिव के केवल ग्रेडिएंट और मैट्रिक्स की गणना करने की आवश्यकता होती है। प्रारंभिक मूल्यों को संभावित मूल्यों और मापदंडों की भिन्नता की सीमा पर उपलब्ध प्राथमिक डेटा को ध्यान में रखते हुए चुना जाता है, और इन डेटा की पूर्ण अनुपस्थिति में उन्हें शून्य (,) के रूप में लिया जाता है।

स्वतंत्र मूल्यों के लिए, आवर्ती संबंधों की प्रणाली (7.5.27) स्पष्ट रूप से एक बहुआयामी (आयाम) मार्कोव यादृच्छिक प्रक्रिया का वर्णन करती है, जिसका घटक पैरामीटर के वास्तविक मूल्य में परिवर्तित होता है, और घटक फिशर सूचना मैट्रिक्स (7.3) में परिवर्तित होता है। 8), अनुमानित पैरामीटर का सही मूल्य कहां है, और वृद्धि के साथ अनिश्चित काल तक बढ़ता है पी।यदि अनुक्रम एर्गोडिक है तो सिस्टम (7.5.27) में अधिक सामान्य परिस्थितियों में समान अभिसरण गुण होते हैं।

उल्लिखित विधियों में से दूसरा, संभावना फ़ंक्शन के लघुगणक के दूसरे डेरिवेटिव के मैट्रिक्स को उसकी गणितीय अपेक्षा के साथ बदलने पर आधारित है - फिशर सूचना मैट्रिक्स, जिसे ध्यान में रखते हुए (7.5.16), इस प्रकार लिखा जा सकता है:

जहां (7.5.26) के समान है

(7.5.24) में मैट्रिक्स को मैट्रिक्स के साथ प्रतिस्थापित करने पर, हम पुनरावृत्ति संबंध प्राप्त करते हैं

सैक्रिसन द्वारा प्रस्तावित अधिकतम संभावना अनुमानों की अनुमानित गणना के लिए (स्वतंत्र रूप से समान रूप से वितरित के लिए मूल में, जब और। यह पुनरावृत्ति संबंध प्रणाली (7.5.27) से सरल है, क्योंकि इष्टतम वजन मैट्रिक्स को इसके गणितीय द्वारा प्रतिस्थापित किया जाता है अपेक्षा, और इसे खोजने के लिए मौजूदा अवलोकन डेटा की आवश्यकता नहीं है, सिवाय उन लोगों के जो अनुमान के मूल्य में केंद्रित हैं। साथ ही, यह स्पष्ट है कि इस तरह के प्रतिस्थापन का मतलब (7.5) की तुलना में अतिरिक्त आवश्यकता को पूरा करने की आवश्यकता है .27) कि दूसरे डेरिवेटिव का मैट्रिक्स इसकी गणितीय अपेक्षा के करीब है।

यदि संभाव्यता घनत्व फ़ंक्शन और मैट्रिक्स चरण दर चरण बदलते हैं, तो प्रत्येक चरण को सीधे खोजने के लिए बहुत अधिक गणनाओं की आवश्यकता हो सकती है। इस मामले में, छोटे अंतरों की असमानता से शून्य तक निर्धारित परिणामों की सटीकता में अतिरिक्त कमी के कारण, कोई मैट्रिक्स के अनुमानित मूल्य की आवर्ती गणना के लिए आगे बढ़ सकता है। इस अनुमानित मूल्य के लिए पिछले अंकन पर लौटने पर, हमें पुनरावृत्ति संबंधों की एक और प्रणाली प्राप्त होती है

मैट्रिक्स का अपेक्षित मूल्य (एक अवलोकन के लिए फिशर सूचना मैट्रिक्स) बिंदु पर लिया गया। यह प्रणाली (7.5.27) से इस मायने में भिन्न है कि पुनरावृत्ति संबंधों के दूसरे भाग (7.5.31) में सीधे तौर पर अवलोकन संबंधी डेटा शामिल नहीं है।

ऊपर मानी गई पुनरावृत्ति संबंधों की कोई भी प्रणाली पूरी तरह से सटीक है यदि फ़ंक्शन द्विघात रूप से निर्भर करता है, और इसके अतिरिक्त, दूसरे डेरिवेटिव का मैट्रिक्स निर्भर नहीं करता है। वास्तव में, यह एक अज्ञात गणितीय अपेक्षा के साथ स्वतंत्र सामान्य रूप से वितरित (जरूरी नहीं कि समान) मूल्यों के मामले से मेल खाता है, जो अनुमानित पैरामीटर का प्रतिनिधित्व करता है।

पुनरावृत्ति संबंधों की प्रणाली (7.5.24) बहुत व्यापक परिस्थितियों में अधिकतम संभावना समीकरण का सटीक समाधान देती है, केवल इस आवश्यकता के साथ कि फ़ंक्शन द्विघात रूप से निर्भर करता है। इसके अलावा, निर्भरता मनमानी है, जो स्वतंत्र और आश्रित दोनों मूल्यों के साथ जनसंख्या संभाव्यता वितरण की एक विस्तृत श्रेणी से मेल खाती है।

विचार की गई सामान्य विधियों के साथ-साथ, आवर्ती संबंध (7.5.24) में भार गुणांक के मैट्रिक्स का चयन करने के लिए कई विधियां हैं, जो कुछ विशिष्ट प्रतिबंधों के अनुकूल हैं। इनमें से सबसे सरल एक विकर्ण मैट्रिक्स के रूप में विकल्प है, ताकि, ( मैं- यूनिट मैट्रिक्स), जहां संख्यात्मक गुणांकों का घटता क्रम है, जिसे रॉबिन्स-मोनरो स्टोकेस्टिक सन्निकटन प्रक्रिया की तरह ही संभावना फ़ंक्शन के गुणों से स्वतंत्र रूप से चुना जाता है, जिस पर निम्नलिखित अध्यायों में चर्चा की जाएगी।

यह ध्यान देने योग्य है कि अधिकतम संभावना अनुमान खोजने के लिए कोई भी पुनरावृत्त या आवर्ती प्रक्रिया आम तौर पर अनुमानित होती है। इसलिए, सामान्यतया, इन प्रक्रियाओं को लागू करने के परिणामस्वरूप प्राप्त अनुमानों के लिए, स्थिरता, स्पर्शोन्मुख दक्षता और स्पर्शोन्मुख सामान्यता को नए सिरे से सिद्ध किया जाना चाहिए। पुनरावृत्त प्रक्रियाओं के लिए, अनुमानों के आवश्यक गुणों की गारंटी इस तथ्य से होती है कि, सिद्धांत रूप में, ऐसी प्रक्रियाएं, पुनरावृत्तियों की उचित संख्या के साथ, किसी भी पूर्व निर्धारित सटीकता के साथ संभावना समीकरण का समाधान प्रदान करती हैं। आवर्ती प्रक्रियाओं के लिए विशेष प्रमाण हैं जैसे (7.5.27), (7.5.30), (7.5.31) और अन्य। साथ ही, नियमितता की आवश्यकता के अतिरिक्त, कुछ अतिरिक्त आवश्यकताएँ भी लगाई जाती हैं:

|| के विभिन्न मानों के लिए फ़ंक्शन (7.2.2) के व्यवहार पर, एक आवर्ती प्रक्रिया का उपयोग करके, पैरामीटर के वास्तविक मान के अनुरूप बिंदु पर इस फ़ंक्शन का एक वैश्विक अधिकतम प्राप्त करने के लिए;

बड़े निरपेक्ष मानों के लिए संभाव्यता फलन के लघुगणक के व्युत्पन्नों के दूसरे क्षणों में वृद्धि के क्रम से। ये आवश्यकताएं मार्कोव यादृच्छिक प्रक्रिया के घटकों के सभी या कुछ हिस्सों के एक बिंदु पर अभिसरण के लिए अधिक सामान्य स्थितियों का परिणाम हैं, जहां एक या किसी अन्य आवर्ती प्रक्रिया का नेतृत्व होता है।

निष्कर्ष में, हम यह भी ध्यान देते हैं कि ऐसे मामले में जब अधिकतम संभावना समीकरण का सटीक समाधान होता है, इसे लगभग हमेशा आवर्ती रूप में दर्शाया जा सकता है। आइए हम दो सरल भिन्न उदाहरण दें। इस प्रकार, जनसंख्या में एक सामान्य यादृच्छिक चर की अज्ञात गणितीय अपेक्षा का एक प्रारंभिक अनुमान एनअंकगणितीय माध्य के रूप में इसका नमूना मान

अधिकतम संभावना अनुमान है और इसे आवर्ती रूप में दर्शाया जा सकता है:

जो सबसे सरल विशेष मामला (7.5.30) है

एक अन्य उदाहरण पैरामीटर के लिए अनियमित अधिकतम संभावना अनुमान है - आयताकार वितरण की चौड़ाई - (7.4.2) से, जिसे पुनरावृत्ति संबंध द्वारा भी निर्धारित किया जा सकता है

प्रारंभिक शर्त के साथ. यह पुनरावृत्ति संबंध एक अलग प्रकार का है: इसके दाहिने हिस्से को पिछले अनुमान और एक छोटे सुधार के योग के रूप में प्रस्तुत नहीं किया जा सकता है, जो इस उदाहरण की अनियमितता का परिणाम है; हालाँकि, इसमें आवर्ती दृष्टिकोण के सभी फायदे हैं: इसमें पिछले चरण - अनुमान - से सिर्फ एक संख्या को याद रखने की आवश्यकता होती है और सभी मूल्यों की तुलना करने के बजाय खोज को एक तुलना तक कम कर देता है।

दिए गए उदाहरण उस स्थिति में भी आवर्ती तरीकों के फायदों को दर्शाते हैं जब अधिकतम संभावना समीकरण एक सटीक समाधान की अनुमति देता है, क्योंकि परिणाम के विश्लेषणात्मक प्रतिनिधित्व की सादगी इसे प्राप्त करने की कम्प्यूटेशनल सादगी के समान नहीं है।

7.5.3. निरंतर समय में संक्रमण. अधिकतम संभावना अनुमानकों के लिए विभेदक समीकरण

आइए अब उस विशेष मामले पर विचार करें जब अवलोकन डेटा उपलब्ध हो एक्सनमूना बिंदुओं के एक सेट द्वारा वर्णित नहीं हैं , a किसी प्रक्रिया के कार्यान्वयन के एक खंड का प्रतिनिधित्व करता है , अंतराल पर निर्दिष्ट मापदंडों के आधार पर , और अवलोकन के दौरान इस अंतराल की लंबाई बढ़ सकती है (समय बिंदु)। टीपरिवर्तनशील है)।

अवलोकन डेटा के सांख्यिकीय विवरण के लिए, इस मामले में, एक संभावना अनुपात कार्यात्मक पेश किया गया है, जो एक समान संभावना के लिए मनमाने ढंग से दिए गए मूल्य पर मूल्यों के एक सेट के संभाव्यता घनत्व वितरण के अनुपात की अधिकतम सीमा है। एक निश्चित निश्चित मूल्य पर घनत्व, और कुछ मामलों में, जब यह प्रतिनिधित्व की अनुमति देता है, जहां एक यादृच्छिक प्रक्रिया होती है, जो प्रदान किए गए मूल्यों के एक सेट की संभावना घनत्व से स्वतंत्र होती है। संभाव्यता अनुपात कार्यात्मक का उपयोग हमें निरंतर समय पर जाने पर उत्पन्न होने वाली संभाव्यता घनत्व को निर्धारित करने में औपचारिक कठिनाइयों को खत्म करने की अनुमति देता है।

संभाव्यता अनुपात कार्यात्मक के लघुगणक को इस प्रकार दर्शाया जा सकता है

अंतराल पर प्रक्रिया की कुछ कार्यात्मकता कहां है। कुछ मामलों में, फ़ंक्शनल एक ऐसे फ़ंक्शन में परिवर्तित हो जाता है जो केवल के मान पर निर्भर करता है। तो यदि

जहां समय और मापदंडों का एक ज्ञात कार्य है, और वर्णक्रमीय घनत्व के साथ एक डेल्टा-सहसंबद्ध यादृच्छिक प्रक्रिया ("सफेद" शोर) है एनओ, फिर, संभाव्यता वितरण के संभाव्यता अनुपात को हर के रूप में चुनना एक्सके साथ, हमारे पास होगा

मान लीजिए पैरामीटर का अधिकतम संभावना अनुमान है, जो अंतराल पर प्रक्रिया के कार्यान्वयन से निर्मित होता है, यानी अधिकतम संभावना समीकरण का समाधान

समय के संबंध में इस समीकरण के बाएँ पक्ष को विभेदित करने पर, हम प्राप्त करते हैं

पदनामों का परिचय

और समीकरण (7.5.42) को हल करने पर, हमें अधिकतम संभावना का अनुमान लगाने के लिए एक अंतर समीकरण प्राप्त होता है

मैट्रिक्स, बदले में, (7.5.37) के अनुसार अंतर समीकरण द्वारा निर्धारित किया जाता है

असतत मामले की तरह, (7.5.45), (7.5.47) में मैट्रिक्स को इसकी गणितीय अपेक्षा से बदला जा सकता है - के मूल्य पर फिशर सूचना मैट्रिक्स, और वजन के लिए अंतर समीकरण (7.5.46) मैट्रिक्स - समीकरण द्वारा

जहां असतत मामले के समान है

दूसरे डेरिवेटिव के मैट्रिक्स की गणितीय अपेक्षा।

अंतर समीकरणों का सेट (7.5.45), (7.5.46) या (7.5.45), (7.5.48), प्रारंभिक शर्तों के साथ, जिसके विकल्प के संबंध में असतत मामले के लिए कही गई हर बात पूरी तरह से वैध रहती है समय में किसी भी क्षण के लिए अधिकतम संभावना अनुमान निर्धारित करता है। इस सेट को उपयुक्त, आम तौर पर बोलने वाले, गैर-रेखीय एनालॉग उपकरणों का उपयोग करके या उपयुक्त समय नमूने के साथ, कंप्यूटर का उपयोग करके हल किया जा सकता है। अंत में, आइए हम इन समीकरणों के संशोधनों में से एक पर ध्यान दें, जो हमें मैट्रिक्स को उलटने की आवश्यकता से बचने की अनुमति देता है।

पदनाम का परिचय

, कहाँ मैं

और समय के संबंध में संबंध को अलग करना , कहाँ मैंपहचान मैट्रिक्स है, (7.5.46) का उपयोग करके हम एक अंतर समीकरण प्राप्त करते हैं जो सीधे मैट्रिक्स को निर्धारित करता है:

(और इसी तरह जब प्रतिस्थापित किया जाता है), जो समीकरण (7.5.45) के साथ मिलकर

मूल्यांकन निर्धारित करता है , मैट्रिक्स व्युत्क्रमण की आवश्यकता के बिना। इस मामले में, सबसे सरल रैखिक अंतर समीकरण (7.5.46) से रिकाती प्रकार के एक गैर-रेखीय अपेक्षाकृत अंतर समीकरण (7.5.51) में संक्रमण होता है।

सामान्य समाधानपुनरावृत्ति संबंध (1) इस संबंध को संतुष्ट करने वाले सभी अनुक्रमों का समुच्चय है।

निजी निर्णयसंबंध (1) इस संबंध को संतुष्ट करने वाले अनुक्रमों में से एक है।

उदाहरण 1¢.परिणाम को एक=ए 0 +रा एक=एक - 1 +डी. यह अंतर के साथ अंकगणितीय प्रगति के सामान्य पद का सूत्र है डीऔर प्रगति की प्रारंभिक अवधि के साथ ए 0 .

उदाहरण 2¢.परिणाम को बी एन=बी 0 × क्यू.एनसंबंध का एक सामान्य समाधान है बी एन=बी एन - 1 ×q. यह एक हर के साथ ज्यामितीय प्रगति के सामान्य पद का सूत्र है क्यू¹0 और प्रगति के प्रारंभिक पद के साथ बी 0 .

उदाहरण 3¢.तथाकथित बिनेट का सूत्रजे एन=संबंध j का एक विशेष समाधान है एन=जे एन- 2 +जे एन- 1 जब जे 0 =जे 1 =1.

सरल जड़ों के बाद से एक्स 1 ,…,एक्स कजोड़ीवार अलग, फिर D¹0। इसका मतलब है कि सिस्टम (5) में एक (अद्वितीय) समाधान है।

कार्य 1।सूत्र (4) का उपयोग करके ज्यामितीय प्रगति का सामान्य पद ज्ञात कीजिए।

समाधान बी एन=क्यूबन- 1 का फॉर्म है. इसीलिए ।

कार्य 2.फाइबोनैचि संबंध का सामान्य समाधान खोजें एक + 2 =एक+एक + 1 .

समाधान. पुनरावृत्ति संबंध का अभिलक्षणिक बहुपद एक + 2 =एक+एक+1 का रूप है। इसीलिए ।

हम बिना प्रमाण के प्रमेय 1 का निम्नलिखित सामान्यीकरण प्रस्तुत करते हैं।

प्रमेय 2. मान लीजिए कि सजातीय रैखिक पुनरावृत्ति संबंध (3) का अभिलक्षणिक बहुपद है कजड़ें: ए 1 बहुलता, …, ए कबहुलता , , . तब पुनरावृत्ति संबंध (3) का सामान्य समाधान निम्नलिखित रूप में होता है:

कार्य 3.संबंध का सामान्य समाधान खोजें.

समाधान।अभिलक्षणिक बहुपद का मूल गुणज 3 में से 2 होता है। इसलिए।

टिप्पणी. अमानवीय रैखिक संबंध (2) का सामान्य समाधान सजातीय रैखिक संबंध (3) के सामान्य समाधान और अमानवीय रैखिक संबंध (2) के विशेष समाधान के योग के रूप में पाया जा सकता है।

4. कार्य उत्पन्न करना।औपचारिक शृंखला ए 0 +ए 1 एक्स+ए 2 एक्स 2 +…+ए के एक्स के+... बुलाया गया अनुक्रम का जनरेटिंग फ़ंक्शन ए 0 ,ए 1 ,ए 2 ,…,एक क,…

जनक फलन या तो एक अभिसरण श्रृंखला या अपसारी श्रृंखला है। दो अपसारी श्रृंखलाएं फलन के रूप में समान हो सकती हैं, लेकिन अलग-अलग अनुक्रमों के फलन उत्पन्न कर सकती हैं। उदाहरण के लिए, पंक्तियाँ 1+2 एक्स+2 2 एक्स 2 +…+2के एक्स के+… और 1+3 एक्स+3 2 एक्स 2 +…+3के एक्स के+... समान फ़ंक्शन को परिभाषित करें (बिंदु पर 1 के बराबर)। एक्स=1, बिंदुओं पर अपरिभाषित एक्स>1), लेकिन विभिन्न अनुक्रमों के कार्य उत्पन्न कर रहे हैं।

अनुक्रमों के निर्माण कार्यों के गुण:

अनुक्रमों के उत्पन्न कार्यों का योग (अंतर)। एकऔर बी एनअनुक्रमों के योग (अंतर) के जनक फलन के बराबर एक+बी एन;

अनुक्रमों के कार्यों को उत्पन्न करने का उत्पाद एकऔर बी एनअनुक्रमों के संवलन का जनक कार्य है एकऔर बी एन:

सी एन=ए 0 बी एन+ए 1 बी एन - 1 +…+एक - 1 बी 1 +ए एन बी 0 .

उदाहरण 1।फ़ंक्शन अनुक्रम के लिए उत्पन्न हो रहा है

उदाहरण 2.फ़ंक्शन अनुक्रम 1, 1, 1, ... के लिए उत्पन्न हो रहा है

प्रतिलिपि

1 रूसी संघ कोस्त्रोमा के शिक्षा और विज्ञान मंत्रालय स्टेट यूनिवर्सिटीएन. ए. नेक्रासोव टी. एन. मैटित्सिना के नाम पर रखा गया असतत गणित आवर्ती संबंधों का समाधान कार्यशाला कोस्त्रोमा 2010

2 बीबीके या73-5 एम348 केएसयू के संपादकीय और प्रकाशन परिषद के निर्णय द्वारा प्रकाशित। एन. ए. नेक्रासोवा समीक्षक ए. वी. चेरेडनिकोवा, भौतिक और गणितीय विज्ञान के उम्मीदवार, एसोसिएट प्रोफेसर एम348 मैटित्सिना टी. एन. असतत गणित। पुनरावृत्ति संबंधों को हल करना: कार्यशाला [पाठ] / टी.एन. मैटित्सिना। कोस्त्रोमा: केएसयू के नाम पर रखा गया। एन. ए. नेक्रासोवा, पी. कार्यशाला में छात्रों के लिए व्यक्तिगत असाइनमेंट शामिल हैं और इसका उद्देश्य "असतत गणित" पाठ्यक्रम के पहले भाग में महारत हासिल करने के लिए स्वतंत्र कार्य सुनिश्चित करना है। भौतिकी और गणित संकाय के दूसरे तीसरे वर्ष के छात्रों के लिए, एक अतिरिक्त विशेषता "सूचना विज्ञान" के साथ "गणित" विशेषता में अध्ययन, एक अतिरिक्त विशेषता "गणित" के साथ "सूचना विज्ञान"। BBK ya73-5 T. N. Matytsina, 2010 KSU के नाम पर रखा गया। एन. ए. नेक्रासोवा,

3 सामग्री परिचय रैखिक आवर्ती संबंधों को हल करने के लिए पद्धतिगत सिफारिशें आवर्तक (वापसी) अनुक्रमों की मूल अवधारणाएं और परिभाषाएं एलओआरएस और एलआरएस को हल करने के लिए एल्गोरिदम एलओआरएस और एलआरएस समस्याओं को हल करने के उदाहरण स्वतंत्र निर्णयएलओआरएस और एलआरएस उत्तरों को हल करने के लिए समस्याएं निष्कर्ष ग्रंथ सूची

4 परिचय पाठ्यक्रम का पहला भाग "असतत गणित", भौतिकी और गणित संकाय के दूसरे तीसरे वर्ष के छात्रों द्वारा अध्ययन किया जाता है, एक अतिरिक्त विशेषता "गणित" (चतुर्थ सेमेस्टर) और "गणित" के साथ "सूचना विज्ञान" विशेषता में अध्ययन किया जाता है। एक अतिरिक्त विशेषता "सूचना विज्ञान" (पांचवें सेमेस्टर) में पुनरावृत्ति संबंधों को हल करना शामिल है। इस संस्करण में सजातीय और अमानवीय रैखिक पुनरावृत्ति संबंधों की गणना के लिए समस्याएं शामिल हैं। कार्यशाला लिखने का कारण यह तथ्य था कि छात्रों के पास इस पाठ्यक्रम में समस्याओं को हल करने में व्यावहारिक रूप से कोई कौशल नहीं है। एक कारण सुलभ पाठ्यपुस्तक या समस्याओं के संग्रह की कमी है। प्रस्तावित कार्यशाला के कार्य प्रत्येक छात्र को (व्यक्तिगत रूप से) समस्याओं को हल करने के बुनियादी तरीकों और तकनीकों को समझने में मदद करेंगे। सामग्री में महारत हासिल करना आसान बनाने के लिए, मैनुअल की शुरुआत में स्वतंत्र समाधान के लिए प्रस्तावित सभी प्रकार की समस्याओं पर विचार किया जाता है। अंत में अनुशंसित साहित्य की एक सूची है जो आपको इस विषय का अधिक गहराई से अध्ययन करने में मदद करेगी। विषय "पुनरावृत्ति संबंध" स्कूल के पाठ्यक्रम (अंकगणित और ज्यामितीय प्रगति, प्राकृतिक संख्याओं के वर्गों और घनों का क्रम, आदि) के करीब है, और इसलिए छात्रों को पहले किसी अन्य विषयों का अध्ययन करने की आवश्यकता नहीं है। आवर्ती संबंधों (वापसी अनुक्रम) के सिद्धांत के मूल सिद्धांतों को 20 के दशक में विकसित और प्रकाशित किया गया था। XVIII सदी फ्रांसीसी गणितज्ञ ए. मोइवरे और सेंट पीटर्सबर्ग एकेडमी ऑफ साइंसेज के पहले सदस्यों में से एक, स्विस गणितज्ञ डी. बर्नौली। 18वीं शताब्दी के महानतम गणितज्ञ द्वारा एक विस्तृत सिद्धांत दिया गया था। 4

5 सेंट पीटर्सबर्ग के शिक्षाविद एल. यूलर। बाद के कार्यों में, प्रसिद्ध रूसी गणितज्ञ शिक्षाविदों पी. एल. चेबीशेव और ए. ए. मार्कोव द्वारा दिए गए परिमित अंतरों की गणना पर पाठ्यक्रमों में पारस्परिक अनुक्रमों के सिद्धांत की प्रस्तुति पर प्रकाश डालना उचित है। पुनरावृत्ति संबंध (लैटिन शब्द रिकरेरे से रिटर्न तक) असतत गणित में एक बड़ी भूमिका निभाते हैं, अनिवार्य रूप से, एक अर्थ में, अंतर समीकरणों का एक अलग एनालॉग होते हैं। इसके अलावा, वे आपको किसी दी गई समस्या को पैरामीटर से घटाकर 1 पैरामीटर से समस्या में, फिर 2 पैरामीटर से समस्या में बदलने आदि की अनुमति देते हैं। पैरामीटर की संख्या को क्रमिक रूप से कम करके, आप एक ऐसी समस्या तक पहुंच सकते हैं जिसे हल करना आसान है। पुनरावृत्ति संबंध (वापसी अनुक्रम) की अवधारणा अंकगणित या ज्यामितीय प्रगति की अवधारणा का एक व्यापक सामान्यीकरण है। विशेष मामलों के रूप में, इसमें प्राकृतिक संख्याओं के वर्गों या घनों के अनुक्रम, एक तर्कसंगत संख्या के दशमलव विस्तार के अंकों के अनुक्रम (और सामान्य तौर पर किसी भी आवधिक अनुक्रम), बढ़ते क्रम में व्यवस्थित दो बहुपदों के विभाजन के भागफल के गुणांक के अनुक्रम भी शामिल हैं। x आदि की शक्तियाँ 5

6 1. रैखिक आवर्ती संबंधों को हल करने के लिए पद्धति संबंधी सिफारिशें 1.1. आवर्ती (वापसी) अनुक्रमों की बुनियादी अवधारणाएँ और परिभाषाएँ हम अनुक्रमों को ए 1, ए 2, ए 3, ए, (1) या, संक्षेप में, (ए) के रूप में लिखेंगे। यदि कोई प्राकृतिक संख्या k और संख्याएँ α 1, α 2, α k (वास्तविक या काल्पनिक) हैं, जैसे कि, एक निश्चित संख्या से शुरू होकर और बाद की सभी संख्याओं के लिए, a +k = α 1 a +k 1 + α 2 a + k α k a, (k 1), (2) तो अनुक्रम (1) को क्रम k का आवर्तक (वापसी) अनुक्रम कहा जाता है, और संबंध (2) को क्रम k का आवर्तक (वापसी) समीकरण कहा जाता है। इस प्रकार, एक आवर्ती अनुक्रम की विशेषता इस तथ्य से होती है कि इसके प्रत्येक सदस्य (उनमें से कुछ से शुरू) को सूत्र (2) के अनुसार तुरंत पूर्ववर्ती सदस्यों की समान संख्या k के माध्यम से व्यक्त किया जाता है। "आवर्ती" (साथ ही आवर्ती) नाम का उपयोग सटीक रूप से किया जाता है क्योंकि यहां, बाद के पद की गणना करने के लिए, वे पिछले शब्दों पर लौटते हैं। आइए आवर्ती अनुक्रमों के कुछ उदाहरण दें। उदाहरण 1. ज्यामितीय प्रगति। आइए एक ज्यामितीय प्रगति देखें: a 1 = α, a 2 = α q, a 3 = α q 2, a = α q 1, ; (3) इसके लिए, समीकरण (2) रूप लेता है: ए +1 = क्यू ए। (4) 6

7 यहाँ k = 1 और α 1 = q है। इस प्रकार, एक ज्यामितीय प्रगति एक प्रथम-क्रम आवर्ती अनुक्रम है। उदाहरण 2. अंकगणितीय प्रगति. अंकगणितीय प्रगति के मामले में a 1 = α, a 2 = α + d, a 3 = α + 2d, a = α + (1)d, हमारे पास +1 = a + d एक ऐसा संबंध है जिसमें यह नहीं है समीकरण का रूप (2). हालाँकि, यदि हम दो आसन्न मानों के लिए लिखे गए दो संबंधों पर विचार करते हैं: a +2 = a +1 + d और a +1 = a + d, तो हम पद-दर-पद घटाव द्वारा उनसे प्राप्त करते हैं a +2 a +1 = a +1 ए, या ए +2 = 2ए +1 (2) के रूप का एक समीकरण। यहाँ k = 2, α 1 = 2, α 2 = 1। इसलिए, एक अंकगणितीय प्रगति एक दूसरे क्रम का आवर्ती अनुक्रम है। उदाहरण 3. खरगोशों की संख्या के बारे में प्राचीन फाइबोनैचि समस्या 1 पर विचार करें। इसमें वर्ष के दौरान एक जोड़े से बनने वाले परिपक्व खरगोशों के जोड़े की संख्या निर्धारित करने की आवश्यकता होती है, यदि यह ज्ञात हो कि खरगोशों का प्रत्येक परिपक्व जोड़ा हर महीने एक नए जोड़े को जन्म देता है, और नवजात शिशु एक महीने के भीतर पूर्ण परिपक्वता तक पहुंच जाते हैं। इस समस्या में जो दिलचस्प है वह परिणाम नहीं है, जिसे प्राप्त करना बिल्कुल भी मुश्किल नहीं है, बल्कि अनुक्रम है, जिसके शब्द प्रारंभिक क्षण में खरगोशों के परिपक्व जोड़े की कुल संख्या को व्यक्त करते हैं (ए 1) एक महीने के बाद (ए) 2), दो महीने के बाद (ए 3) और, सामान्य तौर पर, महीनों के बाद (ए +1)। यह स्पष्ट है कि 1 = 1. एक महीने में नवजात शिशुओं का एक जोड़ा जोड़ा जाएगा, लेकिन परिपक्व जोड़ों की संख्या समान होगी: 2 = 1. दो महीने के बाद, खरगोश परिपक्वता तक पहुंच जाएंगे और कुल संख्या परिपक्व जोड़े दो के बराबर होंगे: a 3 = 2. आइए पहले ही मात्रा 1 फाइबोनैचि, या पीसा के लियोनार्डो, एक इतालवी मध्ययुगीन गणितज्ञ (लगभग 1200) ने एक पुस्तक "ऑन द अबेकस" छोड़ दी है, जिसमें व्यापक अंकगणित और बीजगणित शामिल है। जानकारी मध्य एशिया और बीजान्टिन के लोगों से उधार ली गई और रचनात्मक रूप से उनके द्वारा संशोधित और विकसित की गई। 7

1 महीने में 8 परिपक्व जोड़े और महीने में +1। चूँकि इस समय तक पहले से मौजूद परिपक्व जोड़े दूसरे जोड़े को संतान देंगे, तो + 1 महीने के बाद परिपक्व जोड़ों की कुल संख्या होगी: a +2 = a +1 + a। (6) अतः a 4 = a 3 + a 2 = 3, a 5 = a 4 + a 3 = 5, a 6 = a 5 + a 4 = 8, a 7 = a 6 + a 5 = 13,। इस प्रकार हमने अनुक्रम प्राप्त किया a 1 = 1, a 2 = 1, a 3 = 2, a 4 = 3, a 5 = 5, a 6 = 8, a 7 = 13, a 13 = 233, (7) जिसमें प्रत्येक अगला पद पिछले दो के योग के बराबर है। इस अनुक्रम को फाइबोनैचि अनुक्रम कहा जाता है, और इसके सदस्यों को फाइबोनैचि संख्याएँ कहा जाता है। समीकरण (6) से पता चलता है कि फाइबोनैचि अनुक्रम एक दूसरे क्रम का आवर्ती अनुक्रम है। उदाहरण 4. अगले उदाहरण के रूप में, प्राकृतिक संख्याओं के वर्गों के अनुक्रम पर विचार करें: a 1 = 1 2, a 2 = 2 2, a 3 = 3 2, a = 2,। (8) यहां a +1 = (+ 1) 2 = और, इसलिए, a +1 = a (9) एक से बढ़ने पर, हमें मिलता है: a +2 = a (10) और, इसलिए (पद दर पद घटाने पर ( 9) (10) से), ए +2 ए +1 = ए +1 ए + 2, या ए +2 = 2ए +1 ए + 2। (11) समानता (11) में एक से वृद्धि करने पर, हमारे पास है: ए +3 = 2ए +2 ए ; (12) जहां से ((12) से पद दर पद (11) घटाने पर) a +3 a +2 = 2a +2 3a +1 + a, 8

9 या ए +3 = 3ए +2 3ए +1 + ए। (13) हमने तीसरे क्रम का पुनरावृत्ति समीकरण प्राप्त किया है। इसलिए, अनुक्रम (8) एक तीसरे क्रम का आवर्ती अनुक्रम है। उदाहरण 5. प्राकृतिक संख्याओं के घनों के अनुक्रम पर विचार करें: a 1 = 1 3, a 2 = 2 3, a 3 = 3 3, a = 3,। (14) उदाहरण 4 की तरह ही, हम यह सत्यापित कर सकते हैं कि प्राकृतिक संख्याओं के घनों का क्रम चौथे क्रम का आवर्ती क्रम है। इसके पद समीकरण a +4 = 4a +3 6a a +1 a को संतुष्ट करते हैं। (15) सरलतम आवर्ती अनुक्रमों के मामले में, उदाहरण के लिए, अंकगणित और ज्यामितीय प्रगति, प्राकृतिक संख्याओं के वर्गों या घनों का एक क्रम, हम पिछले सदस्यों की गणना का सहारा लिए बिना अनुक्रम के किसी भी सदस्य को पा सकते हैं। फाइबोनैचि संख्याओं के अनुक्रम के मामले में, पहली नज़र में, हमारे पास ऐसा करने का अवसर नहीं है और, तेरहवीं फाइबोनैचि संख्या 13 की गणना करने के लिए, हम पहले, एक के बाद एक, सभी पिछले शब्दों को ढूंढते हैं (का उपयोग करके) समीकरण a +2 = a +1 + a (6)): a 1 = 1, a 2 = 1, a 3 = 2, a 4 = 3, a 5 = 5, a 6 = 8, a 7 = 13 , ए 8 = 21, ए 9 = 34, ए 10 = 55, ए 11 = 89, ए 12 = 144, ए 13 = 233। आवर्ती अनुक्रम के सदस्यों की संरचना के विस्तृत अध्ययन के दौरान, यह ऐसे सूत्र प्राप्त करना संभव है जो किसी को, सबसे सामान्य मामले में, पिछले सदस्यों की गणना का सहारा लिए बिना आवर्ती अनुक्रम के किसी भी सदस्य की गणना करने की अनुमति देता है। दूसरे शब्दों में, अगला कार्य अनुक्रम के वें पद के लिए एक सूत्र खोजना है जो केवल संख्या पर निर्भर करता है। 9

10 सामान्य स्थिति में पुनरावृत्ति संबंध को a +k = F(, a +k 1, a +k 2, a) के रूप में लिखा जा सकता है, जहां F, k + 1 चर का एक फलन है, और संख्या k को कहा जाता है संबंध का क्रम. पुनरावृत्ति संबंध का समाधान एक संख्यात्मक अनुक्रम b 1, b 2, b 3, b है, जिसके लिए समानता है: b +k = F(, b +k 1, b +k 2, b) किसी भी = 0 के लिए , 1, 2, . सामान्यतया, एक मनमाना पुनरावृत्ति संबंध के अनंत रूप से कई समाधान होते हैं। उदाहरण के लिए, यदि हम दूसरे क्रम के पुनरावृत्ति संबंध +2 = ए +1 + ए पर विचार करते हैं, तो, फाइबोनैचि अनुक्रम के अतिरिक्त: 1, 1, 2, 3, 5, 8, 13, 21, 34,। .., इसकी विशेषता यह है कि यहां 1 = ए 2 = 1, ए 1 और ए 2 के विभिन्न विकल्पों के साथ प्राप्त अन्य अनुक्रमों की अनंत संख्या को संतुष्ट करता है। इसलिए, उदाहरण के लिए, ए 1 = 3 और ए 2 = 1 के साथ हमें अनुक्रम प्राप्त होता है: 3, 1, 2, 1, 3, 4, 7, 11, 18, 29,। पुनरावृत्ति संबंध के समाधान को विशिष्ट रूप से निर्धारित करने के लिए, प्रारंभिक शर्तों को निर्दिष्ट करना आवश्यक है (पुनरावृत्ति संबंध के क्रम के समान ही प्रारंभिक शर्तें होनी चाहिए)। पुनरावृत्ति संबंध को हल करने का अर्थ अनुक्रम के वें पद के लिए सूत्र खोजना है। दुर्भाग्य से, यह अस्तित्व में नहीं है सामान्य विधिमनमाना पुनरावृत्ति संबंधों का समाधान। एक अपवाद स्थिर गुणांक वाले तथाकथित रैखिक पुनरावृत्ति संबंधों का वर्ग है। a +k = α 1 a +k 1 + α 2 a +k α k a के रूप का पुनरावृत्ति संबंध, जहां a i कुछ संख्याएं हैं, i = 1, 2, k, को रैखिक सजातीय पुनरावृत्ति संबंध (LOHR) कहा जाता है क्रम k के स्थिर गुणांक। 10

11 a +k = α 1 a +k 1 + α 2 a +k α k a + f() के रूप का एक आवर्ती संबंध, जहां a i कुछ संख्याएं हैं, i = 1, 2, k, f() 0 एक फ़ंक्शन का, क्रम k के स्थिर गुणांक के साथ रैखिक आवर्तक संबंध (LRS) कहा जाता है, LORS को हल करने के लिए एल्गोरिदम और LORS को हल करने के लिए LRS एल्गोरिदम। हमारे पास एलओआरएस है: ए +के = α 1 ए +के 1 + α 2 ए +के α के ए। 1 कदम. क्रम k का प्रत्येक LORS समान गुणांक वाले डिग्री k के बीजगणितीय समीकरण से मेल खाता है, और इसे LORS का विशेषता समीकरण कहा जाता है। हम अभिलक्षणिक समीकरण x k = α 1 x k 1 + α 2 x k α k x 0 बनाते हैं और इसके मूल x i पाते हैं, जहाँ i = 1, k है। चरण दो। यदि x i मूल बहुलता 1 के हैं (अर्थात, सभी एक दूसरे से भिन्न हैं), तो LORS के सामान्य समाधान का रूप इस प्रकार है: a = c 1 (x 1) + c 2 (x 2) + c 3 (x 3) + + c k (x k ) = c i x i यदि x i बहुलता r i के मूल हैं, तो LORS के सामान्य समाधान का रूप k a = i= 1 (c 1 2 ri 1 i1 + ci2 + ci cir) होता है (उदाहरण के लिए, यदि मूल x गुणन 2 का है, तो a = (c 1 + c 2) x). i x i k i= 1 3 चरण। प्रारंभिक स्थितियों का उपयोग करके गुणांक c i पाए जाते हैं। ग्यारह

एलआरएस को हल करने के लिए 12 एल्गोरिदम। हमारे पास LRS है: a +k = α 1 a +k 1 + α 2 a +k α k a + f()। फ़ंक्शन f() को R m () λ के रूप में दर्शाया जा सकता है, जहां R m () चर में डिग्री m का एक बहुपद है। वास्तव में, उदाहरण के लिए: f() = 10 3= (10 3)1 = R 1() 1, या f() = = (2 + 3) 3 = R 2() 3। आइए हम LRS को फिर से लिखें प्रपत्र a + k α 1 a +k 1 α 2 a +k 2 α k a = R m () λ। 1 कदम. हम संबंधित LORS लिखते हैं: a +k α 1 a +k 1 α 2 a +k 2 α k a = 0 और इसका सामान्य समाधान ढूंढते हैं। ऐसा करने के लिए, हम विशिष्ट समीकरण x k α 1 x k 1 α 2 x k 2 α k x 0 = 0 बनाते हैं और इसके मूल x i पाते हैं, जहां i = 1, k है। उदाहरण के लिए, मान लें कि x i अलग-अलग जड़ें हैं, तो संबंधित LORS के सामान्य समाधान का रूप इस प्रकार है: a = c 1 (x 1) + c 2 (x 2) + c 3 (x 3) + + c k (x k) . चरण दो। हम एलआरएस के लिए एक विशेष समाधान ढूंढते हैं: ए) यदि λ विशेषता समीकरण x k α 1 x k 1 α 2 x k 2 α k = 0 का मूल नहीं है, तो a = Q m () λ, जहां Q m () है चर में घात m का बहुपद; बी) यदि λ विशेषता समीकरण x k α 1 x k 1 α 2 x k 2 α k = 0 बहुलता r का मूल है, तो a = r Q m () λ, जहां Q m () घात m का एक बहुपद है परिवर्तनशील. इसके बाद, हम मूल LRS में a प्रतिस्थापित करते हैं और बहुपद Q m () में गुणांक पाते हैं। 12

13 तीसरा चरण. हम एलआरएस का सामान्य समाधान पाते हैं; यह संबंधित एलआरएस ए के सामान्य समाधान और एलआरएस ए के विशेष समाधान का योग है, यानी ए = ए + ए। प्रारंभिक स्थितियों का उपयोग करके गुणांक c i पाए जाते हैं। LORS और LRS को हल करने के उदाहरण LORS और LRS के समाधान खोजने के लिए दिए गए एल्गोरिदम का उपयोग करके, हम कई समस्याओं का विश्लेषण करेंगे। समस्या 1. दूसरे क्रम के रैखिक सजातीय पुनरावृत्ति संबंध का समाधान खोजें: a +2 = 6 a +1 8 a, a 0 = 3, a 1 = हम विशेषता समीकरण x 2 = 6 x 8 x 0 बनाते हैं और इसकी जड़ें खोजें. x 2 6x + 8 = 0; x 1 = 2, x 2 = 4 मूल भिन्न हैं, इसलिए, उनकी बहुलता LORS का सामान्य समाधान खोजने के बराबर है: a = c 1 (x 1) + c 2 (x 2) = c c चूंकि प्रारंभिक शर्तें दी गई हैं , तो गुणांक c 1 और c 2 विशिष्ट रूप से निर्धारित किए जाते हैं। ए 0 = सी सी = सी 1 + सी 2 = 3; ए 1 = सी सी = 2सी 1 + 4सी 2 = 4। हमें सिस्टम मिलता है: सी1 + सी2 = 3, 2सी1 + 4सी2 = 4। इसे हल करने पर, हम गुणांक पाते हैं: सी 1 = 8, सी 2 = 5। इस प्रकार, LORS के समाधान का प्रकार a = समस्या 2 है। एक रैखिक सजातीय पुनरावृत्ति संबंध का समाधान खोजें: 13

14 ए +2 = 6 ए +1 9 ए, ए 0 = 5, ए 1 = हम अभिलक्षणिक समीकरण x 2 = 6x 9 बनाते हैं और इसके मूल ज्ञात करते हैं। x 2 6x + 9 = 0; (एक्स 3) 2 = 0; x 1 = x 2 = 3 दो मूल, जबकि x 1 और x 2 संपाती हैं, इसलिए, मूल की बहुलता LORS का सामान्य समाधान खोजने के बराबर है: a = (c 1 + c 2) (x 1) = ( सी 1 + सी 2) प्रारंभिक स्थितियों का उपयोग करते हुए, हम गुणांक सी 1 और सी 2 निर्धारित करते हैं: ए 0 = (सी 1 + सी 2 0) 3 0 = सी 1 = 5; a 1 = (c 1 + c 2 1) 3 1 = (c 1 + c 2) 3 = 6। हमें सिस्टम c1 = 5, c1 + c2 = 2 मिलता है। इसे हल करने पर, हम गुणांक c 1 = 5 पाते हैं। , सी 2 = 3। इस प्रकार, एलओआरएस के समाधान का रूप है: ए = (5 3) 3। टिप्पणी। जैसा कि ज्ञात है, एक द्विघात समीकरण की जड़ें तर्कसंगत, अपरिमेय, जटिल संख्याएं आदि हो सकती हैं। ऐसी जड़ों के साथ रैखिक पुनरावृत्ति संबंधों को हल करने की विधि इसी तरह से हल की जाती है। समस्या 3. तीसरे क्रम के रैखिक सजातीय पुनरावृत्ति संबंध का समाधान खोजें: a +3 = 3 a a +1 8 a, a 0 = 9, a 1 = 9, a 2 = हम विशेषता समीकरण x 3 = 3 बनाते हैं x x 8 और इसके मूल ज्ञात कीजिए। x 3 3x 2 6x + 8 = 0; (x 1)(x + 2)(x 4) = 0; x 1 = 1, x 2 = 2, x 3 = 4 मूल अलग-अलग हैं, इसलिए, उनकी बहुलता बराबर है LORS का सामान्य समाधान खोजें: a = c 1 (x 1) + c 2 (x 2) + c 3 ( x 3) = सी सी 2 (2) + सी

15 3. प्रारंभिक स्थितियों का उपयोग करते हुए, हम गुणांक सी 1, सी 2 और सी 3 पाते हैं। ए 0 = सी सी 2 (2) 0 + सी = सी 1 + सी 2 + सी 3 = 9; ए 1 = सी सी 2 (2) 1 + सी = सी 1 2सी 2 + 4सी 3 = 9; a 2 = c c 2 (2) 2 + c = c 1 + 4c c 3 = 9. c1 + c2 + ñ3 = 9, सिस्टम c1 2c2 + 4c3 = 9 को हल करने पर, हमें c 1 = 7, c 2 = 4 प्राप्त होता है , c 3 = 2. इस प्रकार c1 + 4c2 + 16c3 = 9, इस प्रकार, LORS के समाधान का रूप है: a = (2) 2 4. समस्या 4. तीसरे क्रम के रैखिक सजातीय पुनरावृत्ति संबंध का समाधान खोजें : a +3 = a a +1 3 a, a 0 = 6, a 1 = 15, a 2 = हम अभिलाक्षणिक समीकरण x 3 = x 2 + 5x 3 बनाते हैं और इसके मूल ज्ञात करते हैं। एक्स 3 + एक्स 2 5एक्स + 3 = 0; (एक्स 1) 2 (एक्स + 3) = 0; x 1 = x 2 = गुणज 2 का 1 मूल; x 3 = 3 बहुलता का मूल एलओआरएस का सामान्य समाधान खोजें: ए = (सी 1 + सी 2) (एक्स 1) + सी 3 (एक्स 3) = (सी 1 + सी 2) 1 + सी 3 (3)। 3. प्रारंभिक स्थितियों का उपयोग करते हुए, हम गुणांक सी 1, सी 2 और सी 3 पाते हैं। ए 0 = (सी 1 + सी 2 0) सी 3 (3) 0 = सी 1 + सी 3 = 6; ए 1 = (सी 1 + सी 2 1) सी 3 (3) 1 = सी 1 + सी 2 3सी 3 = 15; a 2 = (c 1 + c 2 2) c 3 (3) 2 = c 1 + 2c 2 + 9c 3 = 8. c1 + ñ3 = 6, सिस्टम c1 + c2 3c3 = 15 को हल करने पर, हमें c 1 = प्राप्त होता है 8, सी 2 = 1 और सी 3 = 2। इस प्रकार सी1 + 2सी2 + 9सी3 = 8, इस प्रकार, एलओआरएस के समाधान का रूप है: ए = (8 +) 1 2 (3)। 15

16 समस्या 5. दूसरे क्रम के रैखिक पुनरावृत्ति संबंध का समाधान खोजें: आइए एलआरएस को a +2 = 18 a a + 128, a 0 = 5, a 1 = 2. a a a = () 1 के रूप में फिर से लिखें। संगत LRS लिखें: a a a = 0. अभिलक्षणिक समीकरण बनाएं और उसके मूल ज्ञात करें। x 2 18x + 81 = 0; (x 9) 2 = 0; x 1 = x 2 = 9 विशेषता समीकरण की जड़ें मेल खाती हैं, इसलिए, उनकी बहुलता 2 है। फिर सामान्य समाधान a = (c 1 + c 2) (x 1) = (c 1 + c 2) एक विशेष समाधान खोजें एलआरएस का समाधान. शर्त के अनुसार, f() = R m () λ = = = R 0 () λ, जहां R 0 () = 128 एक चर में एक शून्य-डिग्री बहुपद है, और λ = 1 विशेषता समीकरण का मूल नहीं है संगत LORS का. फलस्वरूप, a = Q m () λ = Q 0 () 1, जहां Q 0 () चर में घात शून्य का एक बहुपद है, in सामान्य रूप से देखेंप्र0 () = स. इस प्रकार, a = c 1. इसके बाद, हम मूल LRS () में a प्रतिस्थापित करते हैं और बहुपद Q 0 () में गुणांक c पाते हैं: c c c 1 = ; सी 18सी + 81सी = 128; 64सी = 128; с = 2. इसलिए, हमें a = с 1 = 2 1 = 2. 16 मिला

17 3. हम एलआरएस का सामान्य समाधान पाते हैं, यह संबंधित एलआरएस ए के सामान्य समाधान और एलआरएस ए के विशेष समाधान का योग है, यानी, ए = ए + ए = (सी 1 + सी 2) प्रारंभिक शर्तों 2 का उपयोग करके गुणांक सी 1 और सी ढूंढना बाकी है। ए 0 = (सी 1 + सी 2 0) = सी = 5; ए 1 = (सी 1 + सी 2 1) = 9सी 1 + 9सी = 2; सिस्टम c1 + 2 = 5, 9c1 + 9c2 + 2 = 2 को हल करने पर, हमें c 1 = 3, c 2 = 3 प्राप्त होता है। इस प्रकार, LRS के समाधान का रूप है: a = (3 3) समस्या 6. खोजें रैखिक पुनरावृत्ति संबंध का एक समाधान: a +2 = 10 a a , a 0 = 7, a 1 = 50. आइए LRS को a a a = के रूप में फिर से लिखें, संबंधित LRS लिखें: a a a = 0; हम एक अभिलक्षणिक समीकरण बनाते हैं और उसके मूल ज्ञात करते हैं। x 2 10 x + 25 = 0; (x 5) 2 = 0; x 1 = x 2 = 5 बहुलता 2 का मूल। फिर LRS के सामान्य समाधान का रूप इस प्रकार है: a = (c 1 + c 2) (x 1) = (c 1 + c 2) इसका एक विशेष समाधान खोजें एलआरएस. शर्त के अनुसार, f() = R m () λ = 50 5 = R 0 () λ, जहां R 0 () = 50 चर में शून्य डिग्री का एक बहुपद है, और λ = 5 मूल x 1 के साथ मेल खाता है संगत LORS के अभिलक्षणिक समीकरण की बहुलता 2। फलस्वरूप, a = r Q m () λ = = 2 Q 0 () 5, जहां Q 0 () = c चर में घात शून्य का बहुपद है। इस प्रकार, a = 2 s 5. इसके बाद, हम मूल LRS में a प्रतिस्थापित करते हैं और गुणांक c: 17 पाते हैं

18 एस (+ 2) एस (+ 1) एस 2 5 = 50 5 (5 0 से विभाजित करें); 25s (+ 2) 2 50s (+ 1) s 2 = 50; सी() 2सी() + सी2 = 2; सी = 1. इसलिए, ए = 2 सी 5 = हम एलआरएस का सामान्य समाधान लिखते हैं: ए = ए + ए = (सी 1 + सी 2) प्रारंभिक स्थितियों का उपयोग करके, हम गुणांक सी 1, और सी 2 पाते हैं : ए 0 = (सी 1 + सी 2 0) = सी 1 = 7; ए 1 = (सी 1 + सी 2 1) = 5सी 1 + 5सी = 50; सिस्टम c1 = 7, c1 + c2 + 1 = 10 को हल करने पर, हमें c 1 = 7, c 2 = 2 प्राप्त होता है। इस प्रकार, LRS के समाधान का रूप है: a = (7 + 2) = () 5। समस्या 7. एक समाधान खोजें रैखिक पुनरावृत्ति संबंध: a +2 = 6 a +1 8 a , a 0 = 0, a 1 = 11. आइए हम LRS को a +2 6 a a = के रूप में फिर से लिखें हम संगत लिखते हैं एलआरएस: ए +2 6 ए ए = 0; हम एक अभिलक्षणिक समीकरण बनाते हैं और उसके मूल ज्ञात करते हैं। x 2 6x + 8 = 0; x 1 = 2, x 2 = 4 बहुलता के मूल 1 के बराबर। तब LRS के सामान्य समाधान का रूप a = c 1 (x 1) + c 2 (x 2) = c c होता है। LRS का एक विशेष समाधान खोजें . शर्त के अनुसार, f() = R m () λ = = (3 + 2) 1 = R 1 () λ, जहां R 1 () = चर में एक प्रथम-डिग्री बहुपद, और λ = 1 मूल नहीं है संगत LORS के अभिलक्षणिक समीकरण का। नतीजतन, a = Q m () λ = Q 1 () 1, जहां Q 1 () एक चर में प्रथम-डिग्री बहुपद है, सामान्य रूप में Q 1 () = = a + b। तो ए = (ए + बी) 1. 18

19 ए और बी: इसके बाद, हम मूल एलआरएस में ए को प्रतिस्थापित करते हैं और गुणांक (ए (+ 2) + बी) (ए (+ 1) + बी) (ए + बी) 1 = 3 + 2 पाते हैं; 25s (+ 2) 2 50s (+ 1) s 2 = 3 + 2; 3ए + (3बी 4ए) = इस प्रकार, हमने पाया कि दो बहुपद बराबर हैं, और फिर संबंधित गुणांक बराबर हैं: 3ए = 3, ए = 1, 3बी 4ए = 2 बी = 2। इसलिए, ए = (ए + बी ) 1 = हम एलआरएस का सामान्य समाधान लिखते हैं: ए = ए + ए = सी सी (+ 2)। प्रारंभिक स्थितियों का उपयोग करते हुए, हम गुणांक सी 1 और सी 2 पाते हैं: ए 0 = सी सी (0 + 2) = 0; ए 1 = सी सी (1 + 2) = 11; सिस्टम c1 + c2 = 2, 2c1 + 4c2 = 14 को हल करने पर, हमें c 1 = 3, c 2 = 5 मिलता है। इस प्रकार, LRS के समाधान का रूप है: a = समस्या 8. रैखिक पुनरावृत्ति का समाधान खोजें संबंध: a +2 = 5 a +1 6 a + (10 4) 2, a 0 = 5, a 1 = 12। आइए LRS को a +2 5 a a = (10 4) के रूप में फिर से लिखें। संगत लिखें एलआरएस: ए +2 5 ए ए = 0; हम एक अभिलक्षणिक समीकरण बनाते हैं और उसके मूल ज्ञात करते हैं। x 2 5x + 6 = 0; x 1 = 3, x 2 = 2 विभिन्न बहुलताओं के मूल 1. तब LORS के सामान्य समाधान का रूप होता है: a = c 1 (x 1) + c 2 (x 2) = c c

20 2. एलआरएस का एक विशेष समाधान खोजें। शर्त के अनुसार, हमारे पास f() = = R m () λ = (10 4) 2 = R 1 () λ है, जहां R 1 () = (10 4) चर में प्रथम-डिग्री बहुपद है, और λ = 2, तो संबंधित LORS के विशेषता समीकरण की जड़ के साथ मेल खाता है। इसलिए, a = r Q m () λ = 1 Q 1 () 2, जहां Q 1 () एक चर में प्रथम-डिग्री बहुपद है, सामान्य रूप में Q 1 () = a + b। इस प्रकार, हमें a = = (a + b) 2 प्राप्त होता है। इसके बाद, हम मूल संबंध में a को प्रतिस्थापित करते हैं और गुणांक a और b पाते हैं। (+ 2)(ए (+ 2) + बी) (+ 1) (ए (+ 1) + बी) (ए + बी) 2 = = (10 4) 2. इस समीकरण को 2 0 से विभाजित करें: 4(+ 2)(ए (+2) + बी) 10(+ 1) (ए (+ 1) + बी) + 6(ए + बी) = 10 4; 4a + (6a 2b) = इस प्रकार, हमने पाया कि दोनों बहुपद बराबर हैं, और फिर संगत गुणांक भी बराबर हैं: 4a = 4, a = 1, 6a 2b = 10 b = 2. इसलिए, a = (a + b ) 2 = (2) हम एलआरएस का सामान्य समाधान लिखते हैं, अर्थात, ए = ए + ए = सी सी (2) 2। प्रारंभिक स्थितियों का उपयोग करते हुए, हम गुणांक सी 1 और सी 2 पाते हैं। ए 0 = सी सी (0 2) 2 0 = 5; a 1 = c c (1 2) 2 1 = 12. सिस्टम c1 + c2 = 5, 3c1 + 2c2 = 14 को हल करने पर, हमें c 1 = 4, c 2 = 1 प्राप्त होता है। इस प्रकार, LRS के समाधान का रूप है : ए = (2 ) 2 = () 2. 20

21 समस्या 9. रैखिक पुनरावृत्ति संबंध का समाधान खोजें: a +2 = 8 a a , a 0 = 1, a 1 = 7. आइए LRS को a +2 8 a a = () के रूप में फिर से लिखें, हम संगत लिखते हैं एलआरएस: ए +2 8 ए ए = 0 ; हम एक अभिलक्षणिक समीकरण बनाते हैं और उसके मूल ज्ञात करते हैं। x 2 8 x + 16 = 0; x 1 = x 2 = 4 मूल संपाती हैं, इसलिए, मूल की बहुलता 2 है। तब LRS के सामान्य समाधान का रूप होता है: a = (c 1 + c 2) (x 1) = (c 1 + c 2) एलआरएस का एक विशेष समाधान खोजें। शर्त के अनुसार, f() = R m () λ = = () 1 = R 2 () λ, जहां R 2 () = चर में एक द्वितीय-डिग्री बहुपद, और λ = 1 मूल के साथ मेल नहीं खाता है संगत LORS का अभिलक्षणिक समीकरण। इसलिए, a = Q m () λ = Q 2 () 1, जहां Q 2 () चर में दूसरी डिग्री का बहुपद है, सामान्य रूप में Q 2 () = a 2 + b + c। इस प्रकार, a = = (a 2 + b + c) 1. इसके बाद, हम मूल संबंध में a को प्रतिस्थापित करते हैं और गुणांक a, b और c पाते हैं। (ए (+ 2) 2 + बी (+ 2)+ सी) (ए (+ 1) 2 + बी (+ 1) + सी) (ए बी + सी) 1 = () 1 ; ए(+ 2) 2 + बी(+ 2)+ सी 8ए(+ 1) 2 8बी(+ 1) 8सी + 16ए बी + 16सी = = ; 9ए 2 12ए + 9बी 4ए 6बी + 9सी = इस प्रकार, हमने पाया कि दो बहुपद बराबर हैं, और फिर संबंधित गुणांक बराबर हैं: 9ए = 9, 12ए + 9बी = 6, 4ए 6बी + 9सी = 2 ए = 1, बी = 2, सी = 2.21

22 इसलिए, ए = (ए 2 + बी + सी) 1 = हम एलआरएस का सामान्य समाधान लिखते हैं, यानी, ए = ए + ए = (सी 1 + सी 2) ()। प्रारंभिक स्थितियों का उपयोग करते हुए, हम गुणांक सी 1 और सी 2 पाते हैं। ए 0 = (सी 1 + सी 2 0) () = 1; a 1 = (c 1 + c 2 1) () = 7. सिस्टम c1 + 2 = 1, 4c1 + 4c2 + 5 = 7 को हल करने पर, हमें c 1 = 1, c 2 = 2 प्राप्त होता है। इस प्रकार, का समाधान एलआरएस का रूप है: ए = (1 2)

23 2. स्वतंत्र समाधान के लिए कार्य 2.1. एलओआरएस और एलआरएस को हल करने के लिए समस्याएं दूसरे क्रम के रैखिक सजातीय पुनरावृत्ति संबंध 1. ए +2 = 9 ए ए, ए 0 = 2, ए 1 = ए +2 = 3.5 ए +1 2.5 ए, ए 0 = 3.5 , ए 1 = ए +2 = 8 ए ए, ए 0 = 4, ए 1 = ए +2 = 2 ए ए, ए 0 = 3, ए 1 = आई। 5. ए +2 = 10 ए ए, ए 0 = 3, ए 1 = ए +2 = 6 ए ए, ए 0 = 0, ए 1 = 2आई ए +2 = 8 ए ए, ए 0 = 2, ए 1 = ए + 2 = 4 ए ए, ए 0 = 7, ए 1 = ए +2 = ए +1 + ए, ए 0 = 2, ए 1 = ए +2 = 8 ए ए, ए 0 = 8, ए 1 = ए +2 = () ए ए, ए 0 = 7, ए 1 = ए +2 = 5 ए +1 4 ए, ए 0 = 0, ए 1 = ए +2 = 2 ए +1 5 ए, ए 0 = 5, ए 1 = 6i ए +2 = 3 ए ए, ए 0 = 7, ए 1 = ए +2 = 6 ए +1 9 ए, ए 0 = 8, ए 1 = ए +2 = 6 ए ए, ए 0 = 3, ए 1 = 9 2i. 17. ए +2 = ए ए, ए 0 = 4, ए 1 = ए +2 = 14 ए ए, ए 0 = 5, ए 1 = ए +2 = 8 ए ए, ए 0 = 2, ए 1 = ए +2 = 7 ए ए, ए 0 = 5, ए 1 = ए +2 = 2 ए +1 + ए, ए 0 = 2, ए 1 =

24 1 22. ए +2 = ए +1 ए, ए 0 = 4, ए 1 = ए +2 = 4 ए +1 ए, ए 0 = 12, ए 1 = ए +2 = ए ए, ए 0 = 2, ए 1 = ए +2 = 2 ए ए, ए 0 = 8, ए 1 = ए +2 = 6 ए +1 9 ए, ए 0 = 12, ए 1 = ए +2 = 4 ए +1 5 ए, ए 0 = 5, ए 1 = 10 आई ए +2 = 3 ए +1 ए, ए 0 = 8, ए 1 = ए +2 = 14 ए ए, ए 0 = 5, ए 1 = ए +2 = 4 ए ए, ए 0 = 2, ए 1 = ए +2 = 4 ए +1 5 ए, ए 0 = 3, ए 1 = 6 7आई। 32. ए +2 = ए ए, ए 0 = 5, ए 1 = ए +2 = 16 ए ए, ए 0 = 7, ए 1 = ए +2 = 5 ए +1 6 ए, ए 0 = 2, ए 1 = ए +2 = 10 ए ए, ए 0 = 2, ए 1 = 10 4आई ए +2 = 6 ए +1 5 ए, ए 0 = 11, ए 1 = ए +2 = 2 ए ए, ए 0 = 11, ए 1 = ए +2 = 6 ए ए ; ए 0 = 3, ए 1 = 0. तीसरे क्रम के रैखिक सजातीय पुनरावृत्ति संबंध 39. ए +3 = 7 ए ए ए, ए 0 = 1, ए 1 = 3, ए 2 = ए +3 = 4 ए +2 ए + 1 6 ए, ए 0 = 4, ए 1 = 5, ए 2 = ए +3 = 6 ए ए ए, ए 0 = 5, ए 1 = 8, ए 2 = ए +3 = 8 ए ए ए, ए 0 = 4, ए 1 = 31, ए 2 = ए +3 = 5 ए +2 3 ए +1 9 ए, ए 0 = 1, ए 1 = 3, ए 2 = ए +3 = 15 ए ए, ए 0 = 8, ए 1 = 40, ए 2 =

25 45. ए +3 = 27 ए ए, ए 0 = 6, ए 1 = 3, ए 2 = ए +3 = 6 ए ए ए, ए 0 = 15, ए 1 = 32, ए 2 = ए +3 = 15 ए ए ए, ए 0 = 1, ए 1 = 20, ए 2 = ए +3 = 9 ए ए, ए 0 = 0, ए 1 = 4, ए 2 = ए +3 = 2 ए ए +1 6 ए, ए 0 = 4, ए 1 = 5, ए 2 = ए +3 = 4 ए +2 5 ए ए, ए 0 = 2, ए 1 = 6, ए 2 = ए +3 = 6 ए +2 5 ए ए, ए 0 = 4, ए 1 = 2, ए 2 = ए +3 = 3 ए ए, ए 0 = 2, ए 1 = 17, ए 2 = ए +3 = 9 ए ए ए, ए 0 = 1, ए 1 = 3, ए 2 = ए +3 = 6 ए ए +1 6 ए, ए 0 = 13, ए 1 = 31, ए 2 = ए +3 = 5 ए +2 3 ए +1 9 ए, ए 0 = 3, ए 1 = 14, ए 2 = ए +3 = ए ए +1 4 ए, ए 0 = 2, ए 1 = 1, ए 2 = ए +3 = 3 ए ए ए, ए 0 = 2, ए 1 = 3, ए 2 = ए +3 = 12 ए ए ए, ए 0 = 2, ए 1 = 16, ए 2 = ए +3 = 4 ए ए ए, ए 0 = 0.2, ए 1 = 6, ए 2 = ए +3 = 8 ए ए ए, ए 0 = 3, ए 1 = 13, ए 2 = ए +3 = 4 ए ए, ए 0 = 3, ए 1 = 29, ए 2 = ए +3 = 5 ए +2 7 ए ए, ए 0 = 11, ए 1 = 34, ए 2 = ए +3 = 11 ए ए ए , ए 0 = 27, ए 1 = 17, ए 2 = ए +3 = 12 ए ए ए, ए 0 = 1, ए 1 = 37, ए 2 = ए +3 = 3 ए ए ए, ए 0 = 11, ए 1 = 23 , ए 2 = ए +3 = 7 ए ए ए, ए 0 = 3, ए 1 = 6, ए 2 = ए +3 = 4 ए ए ए, ए 0 = 4, ए 1 = 1, ए 2 = 4.; 68. ए +3 = 7 ए ए ए, ए 0 = 1, ए 1 = 0, ए 2 = ए +3 = 5 ए ए ए, ए 0 = 6, ए 1 = 0, ए 2 = ए +3 = 5 ए +2 3 ए ए, ए 0 = 10, ए 1 = 1, ए 2 = ए +3 = 3 ए +2 3 ए +1 + ए, ए 0 = 2, ए 1 = 4, ए 2 = ए +3 = 3 ए ए ए , ए 0 = 6, ए 1 = 5, ए 2 =

26 73. ए +3 = 10 ए ए ए, ए 0 = 0, ए 1 = 1, ए 2 = ए +3 = 8 ए ए ए, ए 0 = 8, ए 1 = 23, ए 2 = ए +3 = 5 ए + 2 8 ए +1 4 ए, ए 0 = 11, ए 1 = 15, ए 2 = ए +3 = ए ए ए, ए 0 = 6, ए 1 = 5, ए 2 = ए +3 = 10 ए ए ए, ए 0 = 1, ए 1 = 2, ए 2 = ए +3 = ए ए ए, ए 0 = 1, ए 1 = 14, ए 2 = ए +3 = 2 ए +2 + ए ए, ए 0 = 10, ए 1 = 1, ए 2 = ए +3 = 5 ए +2 8 ए ए, ए 0 = 9, ए 1 = 9, ए 2 = ए +3 = 8आई ए ए +1 10आई ए, ए 0 = 8, ए 1 = 14आई, ए 2 = 38. प्रथम क्रम के रैखिक पुनरावृत्ति संबंध 82. ए +1 = 4 ए + 6, ए 0 = ए +1 = ए + + 1, ए 0 = ए +1 = 5 ए, ए 0 = ए +1 = 3 ए + 5 2, ए 0 = ए +1 = 3 ए + (4) 5 1, ए 0 = ए +1 = 4 ए + 8 4, ए 0 = ए +1 = 3 ए, ए 0 = 14। रैखिक आवर्तक द्वितीय क्रम संबंध 89. ए +2 = 7 ए ए + 10, ए 0 = 4, ए 1 = ए +2 = 10 ए ए + 32, ए 0 = 1, ए 1 = ए +2 = 6 ए +1 9 ए 2 3, ए 0 = 0, ए 1 = ए +2 = 7 ए ए, ए 0 = 3, ए 1 = ए +2 = 9 ए ए + (18 20) 2, ए 0 = 6, ए 1 = ए + 2 = 8 ए +1 7 ए, ए 0 = 9, ए 1 = ए +2 = 4 ए +1 9 ए, ए 0 = 15, ए 1 = 27 आई ए +2 = 12 ए ए, ए 0 = 13, ए 1 = 6.26

ब्लागोवेशचेंस्क राज्य शैक्षणिक विश्वविद्यालय बीजगणित, ज्यामिति और एमएमएम विभाग 16 अप्रैल, 2011 1 पुनरावृत्ति संबंधों का समाधान परिभाषा एक पुनरावृत्ति संबंध संबंध है

व्याख्यान 3. पुनरावृत्ति संबंधों द्वारा परिभाषित अनुक्रम। सजातीय और अमानवीय रैखिक आवर्तक समीकरण (LORE और LNRU)। LORU और LNRU के सामान्य निर्णय। व्याख्याता - एसोसिएट प्रोफेसर सेलेज़नेवा स्वेतलाना

व्याख्यान: अनुक्रम. सजातीय और अमानवीय रैखिक आवर्तक समीकरण। रैखिक आवर्ती सजातीय और अमानवीय समीकरणों के सामान्य समाधान। व्याख्याता - एसोसिएट प्रोफेसर सेलेज़नेवा स्वेतलाना निकोलायेवना

भाषण। प्राकृतिक तर्क (अनुक्रम) के कार्य। सजातीय और अमानवीय रैखिक आवर्तक समीकरण (LORE और LNRU)। LORU और LNRU के सामान्य निर्णय। उदाहरण व्याख्याता - एसोसिएट प्रोफेसर सेलेज़नेवा स्वेतलाना

आवर्ती समीकरणों का समाधान आइए किसी पूर्णांक को प्रतिस्थापित करते समय किसी अभिव्यक्ति के मूल्य से निरूपित करें। फिर अनुक्रम सदस्यों पर अनुक्रम सदस्य की निर्भरता एफ एफ मूल्यों के साथ

पेन्ज़ा स्टेट पेडागोगिकल यूनिवर्सिटी का नाम वीजी बेलिंस्की ओ ए मोनाखोवा, एन ए ओस्मिनिना के नाम पर रखा गया है औपचारिक श्रृंखला के आवर्ती अनुक्रम बीजगणित विशिष्टताओं के छात्रों के लिए पद्धति संबंधी सिफारिशें

व्याख्यान 3. पुनरावृत्ति संबंधों द्वारा परिभाषित अनुक्रम। सजातीय और अमानवीय रैखिक आवर्तक समीकरण (LORE और LNRU)। LORU और LNRU के सामान्य निर्णय। उदाहरण व्याख्याता - एसोसिएट प्रोफेसर सेलेज़नेवा

शिक्षा और विज्ञान मंत्रालय रूसी संघसंघीय राज्य बजट शैक्षिक संस्थाउच्च व्यावसायिक शिक्षा"साइबेरियाई राज्य औद्योगिक विश्वविद्यालय"

रूसी संघ के परिवहन मंत्रालय संघीय राज्य बजटीय शैक्षिक उच्च शिक्षा संस्थान "रूसी परिवहन विश्वविद्यालय (एमआईआईटी)" "गणितीय विश्लेषण" विभाग

गणित पर व्याख्यान खंड टीएमएम-यू वी चेब्राकोव द थ्योरी ऑफ मैजिक मैट्रिसेस सेंट पीटर्सबर्ग, 00 यूडीसी 5+5 बीबीके सीएच35 आर ई एस ई एन टी आर एस: डॉक्टर ऑफ फिजिक्स एंड मैथमेटिक्स, प्रोफेसर सेंट पीटर्सबर्ग टेक्निकल यूनिवर्सिटी एमए सैल कैंडिडेट

एए किरसानोव कॉम्प्लेक्स नंबर पीएसकोव बीबीके 57 के45 बीजगणित और ज्यामिति विभाग और पीएसपीआई के संपादकीय और प्रकाशन परिषद के निर्णय द्वारा प्रकाशित एसएम किरोव समीक्षक के नाम पर: मेदवेदेवा आईएन, भौतिकी और गणित के उम्मीदवार, एसोसिएट प्रोफेसर

मिखाइलोवा इन्ना अनातोल्येवना गणित और प्राकृतिक विज्ञान संस्थान। बीजगणित और मौलिक कंप्यूटर विज्ञान विभाग। 30 सितंबर, 2018 फाइबोनैचि संख्याओं के उदाहरण फाइबोनैचि संख्याएं 1, 1, 2, 3, 5, 8, 13, 21,...

यूराल संघीय विश्वविद्यालय, गणित और कंप्यूटर विज्ञान संस्थान, बीजगणित और असतत गणित विभाग एक बहुपद परिभाषाओं की अवधारणा एक चर में एक बहुपद रूप की अभिव्यक्ति है

अध्याय 0 अनुक्रम एल्गोरिदम ए- संख्यात्मक अनुक्रम सेट करना ए- अंकगणितीय प्रगति ए- ज्यामितीय प्रगति ए- योग ए-5 अनंत रूप से घटती ज्यामितीय प्रगति

रूसी संघ के शिक्षा और विज्ञान मंत्रालय नोवोसिबिर्स्क राज्य विश्वविद्यालय विशिष्ट शैक्षिक और अनुसंधान केंद्र गणित ग्रेड 0 गणितीय प्रेरण और अनंत संख्यात्मक विधि की विधि

शिक्षा के लिए संघीय एजेंसी, उच्च व्यावसायिक शिक्षा के राज्य शैक्षणिक संस्थान, उख्ता राज्य तकनीकी विश्वविद्यालय (यूएसटीयू) सीमा कार्य पद्धति

संख्यात्मक अनुक्रम. ज्यामितीय प्रगति एक ज्यामितीय प्रगति एक संख्यात्मक अनुक्रम बी है, जिसका पहला पद गैर-शून्य है, और प्रत्येक बाद का पद, दूसरे से शुरू होता है,

संघीय शिक्षा एजेंसी उच्च व्यावसायिक शिक्षा का राज्य शैक्षणिक संस्थान "टवर स्टेट यूनिवर्सिटी" गणित संकाय बीजगणित विभाग

अध्याय 0 परीक्षण कार्य और निर्देश टी-00 एक आवर्ती सूत्र का उपयोग करके अनुक्रम शब्दों की गणना टी-00 एक आवर्ती सूत्र टी-00 तैयार करना एक सामान्य पद का सूत्र टी-004 एक अंकगणितीय प्रगति तैयार करना

6-7 स्कूल वर्ष 6, ग्रेड गणित जटिल संख्या 4 बीजगणितीय समीकरण द्विघात समीकरण स्कूल बीजगणित पाठ्यक्रम में, वास्तविक गुणांक वाले द्विघात समीकरण ax bx c =, a, () पर विचार किया गया

रूसी संघ के शिक्षा और विज्ञान मंत्रालय, उच्च व्यावसायिक शिक्षा के राज्य शैक्षणिक संस्थान, मॉस्को स्टेट यूनिवर्सिटी ऑफ़ मैकेनिकल इंजीनियरिंग II पोस्पेलोव,

व्याख्यान अध्याय सेट और उन पर संचालन एक सेट की अवधारणा एक सेट की अवधारणा गणित की सबसे प्राथमिक अवधारणाओं को संदर्भित करती है जिन्हें सरल लोगों के माध्यम से परिभाषित नहीं किया जाता है। एक सेट को एक संग्रह के रूप में समझा जाता है

गणित पर व्याख्यान. वॉल्यूम. टीएमएम-1 यू. वी. चेब्राकोव मैजिक मैट्रिसेस का सिद्धांत सेंट पीटर्सबर्ग, 010 यूडीसी 511+51 बीबीके सीएच345 समीक्षक: भौतिक और गणितीय विज्ञान के डॉक्टर, प्रोफेसर सेंट पीटर्सबर्ग। तकनीक. विश्वविद्यालय

प्रगति अनुक्रम एक प्राकृतिक तर्क का एक कार्य है.. एक सामान्य शब्द सूत्र द्वारा अनुक्रम निर्दिष्ट करना: a n = f(n), n N, उदाहरण के लिए, a n = n + n + 4, a = 43, a = 47, a 3 = 3,. अनुक्रमण

विभेदक समीकरण सामान्य अवधारणाएँ विभेदक समीकरणों के यांत्रिकी, भौतिकी, खगोल विज्ञान, प्रौद्योगिकी और उच्च गणित की अन्य शाखाओं में असंख्य और विविध अनुप्रयोग हैं (उदाहरण के लिए)

सामग्री परिचय. बुनियादी अवधारणाएँ.... 4 1. वोल्टेरा के अभिन्न समीकरण... 5 गृहकार्य विकल्प.... 8 2. वोल्टेरा के अभिन्न समीकरण का समाधान। 10 होमवर्क विकल्प....11

रूसी संघ निज़नी नोवगोरोड राज्य विश्वविद्यालय के सामान्य और व्यावसायिक शिक्षा मंत्रालय। एन. आई. लोबाचेव्स्की कम्प्यूटेशनल गणित संकाय और साइबरनेटिक्स गणितीय विभाग

भाषण। खरगोश की समस्या. फाइबोनैचि संख्याएं, फाइबोनैचि अनुक्रम, पुनरावृत्ति सूत्र 3. फाइबोनैचि संख्याओं के गुण (ए) रैखिकता (बी) संख्या सैद्धांतिक गुण (सी) योग: एफ + एफ +... + एफ एन, विषम

रैखिक बीजगणित पब्लिशिंग हाउस टीएसटीयू रूसी संघ के शिक्षा और विज्ञान मंत्रालय उच्च व्यावसायिक शिक्षा के राज्य शैक्षिक संस्थान "ताम्बोव राज्य तकनीकी विश्वविद्यालय" रैखिक बीजगणित छात्रों के लिए पद्धति संबंधी निर्देश

टीशिन वी I समाधान के बुनियादी तरीके त्रिकोणमितीय समीकरणजी टीशिन वी I गणित शिक्षकों और छात्रों के लिए वर्ष के गणित शिक्षक व्लादिमीर इवानोविच टीशिन द्वारा तैयार सामग्री टीशिन वी आई बेसिक

उच्च क्रम विभेदक समीकरण. कोनेव वी.वी. व्याख्यान की रूपरेखा. सामग्री 1. बुनियादी अवधारणाएँ 1 2. समीकरण जिन्हें क्रम 2 में कम किया जा सकता है 3. उच्च क्रम के रैखिक अंतर समीकरण

व्याख्यान.7. संख्या की अवधारणा का विस्तार. जटिल संख्याएँ, उन पर संक्रियाएँ सार: व्याख्यान संख्या की अवधारणा को प्राकृतिक से जटिल तक सामान्यीकृत करने की आवश्यकता पर प्रकाश डालता है। बीजगणितीय,

रूसी संघ के शिक्षा और विज्ञान मंत्रालय, उच्च व्यावसायिक शिक्षा के संघीय राज्य बजटीय शैक्षणिक संस्थान "उल्यानोवस्क राज्य तकनीकी विश्वविद्यालय"

व्याख्यान 3 टेलर और मैकलॉरिन श्रृंखला पावर श्रृंखला का अनुप्रयोग पावर श्रृंखला में कार्यों का विस्तार टेलर और मैकलॉरिन श्रृंखला अनुप्रयोगों के लिए, किसी दिए गए फ़ंक्शन को पावर श्रृंखला में विस्तारित करने में सक्षम होना महत्वपूर्ण है, वे कार्य

यूराल संघीय विश्वविद्यालय, गणित और कंप्यूटर विज्ञान संस्थान, बीजगणित और असतत गणित विभाग परिचयात्मक टिप्पणियाँ इस व्याख्यान में हम रैखिक बीजगणित का अध्ययन इस प्रकार शुरू करते हैं,

विषय 2-11: आइजेनवेक्टर और आइजेनवैल्यू ए. हां. ओवस्यानिकोव यूराल फेडरल यूनिवर्सिटी इंस्टीट्यूट ऑफ मैथमेटिक्स एंड कंप्यूटर साइंस डिपार्टमेंट ऑफ अलजेब्रा एंड डिस्क्रीट मैथमेटिक्स अलजेब्रा एंड ज्योमेट्री

नोवोसिबिर्स्क स्टेट यूनिवर्सिटी कॉरेस्पोंडेंस स्कूल गणित विभाग गणितीय प्रेरण की विधि और अनंत संख्यात्मक अनुक्रम 0वीं कक्षा, कार्य के प्रारूपण के लिए असाइनमेंट नियम प्रारंभ करना

नियंत्रण कार्य के लिए कार्य अनुशासन: "बीजगणित" विशेषता: "गणित" पत्राचार पाठ्यक्रम 6 सेमेस्टर द्वारा संकलित: विभाग के प्रमुख ट्रोफिमुक एए कई चर परिणामी बीजगणित में बहुपद

दिशा-निर्देश, समाधान, पूर्णांक समीकरणों के उत्तर। एक अज्ञात के साथ समीकरण.. समाधान. आइए इसे समीकरण में जोड़ें। हमें समानता (4ए बी 4) (ए बी 8) 0 प्राप्त होती है। समानता ए बी 0, जहां ए और बी पूर्णांक हैं, संतुष्ट है,

गणितीय विश्लेषण व्याख्यान का परिचय। सेट की अवधारणा. फ़ंक्शन के मूल गुणों की परिभाषा। बुनियादी प्रारंभिक कार्य सामग्री: सेट सिद्धांत के तत्व वास्तविक संख्याओं का सेट संख्यात्मक

कार्य कार्यक्रमग्रेड 8-9 में छात्रों के लिए बीजगणित में बुनियादी महारत हासिल करने के परिणामों की आवश्यकताओं के आधार पर विकसित किया गया है शैक्षिक कार्यक्रममुख्य सामान्य शिक्षा. कार्य कार्यक्रम की गणना की जाती है

यूराल संघीय विश्वविद्यालय, गणित और कंप्यूटर विज्ञान संस्थान, बीजगणित और पृथक गणित विभाग परिचयात्मक टिप्पणियाँ कई समस्याओं को हल करते समय, संख्यात्मक होना आवश्यक हो जाता है

पहले क्रम के सामान्य विभेदक समीकरण। बुनियादी अवधारणाएँ एक अंतर समीकरण एक समीकरण है जिसमें एक अज्ञात फ़ंक्शन व्युत्पन्न या अंतर चिह्न के तहत प्रकट होता है।

निरंतर गुणांक वाले रैखिक विभेदक समीकरणों की प्रणालियाँ, वें क्रम के एक समीकरण में कमी व्यावहारिक दृष्टिकोण से, स्थिर गुणांक वाले रैखिक सिस्टम बहुत महत्वपूर्ण हैं

रूसी संघ के शिक्षा और विज्ञान मंत्रालय निज़नी नोवगोरोड राज्य विश्वविद्यालय का नाम एनआई लोबचेव्स्की राष्ट्रीय अनुसंधान विश्वविद्यालय एवी लियोन्टीव के नाम पर रखा गया है समस्याओं का संग्रह (गणितीय की विधि)

क्रास्नोयार्स्क क्षेत्र के प्रशासन की शैक्षिक एजेंसी क्रास्नोयार्स्क राज्य विश्वविद्यालय के क्रास्नोयार्स्क राज्य विश्वविद्यालय में प्राकृतिक विज्ञान के पत्राचार स्कूल ग्रेड 10 गणित के अतिरिक्त अध्याय मॉड्यूल 4 समाधान विधियां

रूसी संघ के शिक्षा मंत्रालय, रूसी राज्य तेल और गैस विश्वविद्यालय का नाम आईएम गुबकिन VI इवानोव के नाम पर रखा गया है, "विभेदक समीकरण" विषय का अध्ययन करने के लिए दिशानिर्देश (छात्रों के लिए)

भिन्नात्मक घातांक के साथ शक्ति यदि किसी संख्या की घात का घातांक t भिन्नात्मक है, तो वे t, N, तो परिभाषा के अनुसार गैर-नकारात्मक मानों के लिए (0) ऋणात्मक संख्याओं के लिए (0)< операция возведения

रूसी संघ के कृषि मंत्रालय संघीय राज्य बजटीय शैक्षिक संस्थान उच्च शिक्षा "पर्म राज्य कृषि अकादमी के नाम पर रखा गया है

परिमेय संख्याएँ साधारण भिन्न परिभाषा भिन्न रूप के भिन्नों को साधारण भिन्न कहा जाता है साधारण भिन्न, नियमित और अनुचित परिभाषा भिन्न, उचित यदि< при, где Z, N Z, N Z,

भाषण। 5. अंतर समीकरणों का उपयोग करके असतत रैखिक प्रणालियों का विवरण और विश्लेषण 5.. नियतात्मक प्रभावों के तहत एक-आयामी प्रणाली 5... संकेतों और प्रणालियों का विवरण। संकेतों का विवरण. सिग्नल

इस बिंदु के निष्कर्ष में, हम ध्यान देते हैं कि वे एक ऑर्डर मैट्रिक्स के आइजनवेक्टरों के बारे में भी बात करते हैं, जिसका अर्थ है एक -आयामी स्थान के एक ऑपरेटर के आइगेनवेक्टर जिसका मैट्रिक्स एक निश्चित आधार पर होता है।

परिमेय भिन्नों को एकीकृत करने का व्यावहारिक पाठ एक परिमेय भिन्न, P Q के रूप का एक भिन्न है, जहाँ P और Q बहुपद हैं। एक परिमेय भिन्न को उचित कहा जाता है यदि बहुपद P की घात घात से कम हो

विषय 14 "बीजगणितीय समीकरण और अरैखिक समीकरणों की प्रणालियाँ" घात n वाला एक बहुपद, P n () a 0 n + a 1 n-1 + + a n-1 + a n के रूप का एक बहुपद है, जहाँ a 0, a 1 , एक एन-1, एक एन दी गई संख्याएं, एक 0,

विषय: रैखिक समीकरणों की प्रणालियों का सामान्य सिद्धांत ए. हां. ओवस्यानिकोव यूराल संघीय विश्वविद्यालय गणित और कंप्यूटर विज्ञान संस्थान बीजगणित और असतत गणित बीजगणित और ज्यामिति विभाग

रूसी संघ के शिक्षा और विज्ञान मंत्रालय मॉस्को स्टेट यूनिवर्सिटी ऑफ़ जियोडेसी एंड कार्टोग्राफी (MIIGaiK) दूरस्थ शिक्षा संकाय पत्राचार विभाग `` पद्धतिगत निर्देश,

रूसी संघ के शिक्षा और विज्ञान मंत्रालय संघीय राज्य बजटीय शैक्षिक उच्च शिक्षा संस्थान "सेंट पीटर्सबर्ग राज्य औद्योगिक विश्वविद्यालय"

अवकल समीकरण को हल करें समाधान: आइए विशिष्ट समीकरण बनाएं और हल करें:, दो अलग-अलग वास्तविक मूल प्राप्त होते हैं, जो कुछ करना बाकी है वह सूत्र द्वारा निर्देशित उत्तर लिखना है

व्याख्यान जटिल संख्याएँ फैक्टरिंग बहुपद संख्यात्मक सेट जटिल संख्याओं का सेट वास्तविक गुणांक वाले बहुपद फैक्टरिंग संख्यात्मक सेट सेट

आवर्ती संबंध

आवर्ती संबंध

(अक्षांश से। रिकर-रेंस, जेन। केस रिकरंटिस - रिटर्निंग) - एक ही प्रकार के एफ-लिस, जो एक दूसरे का अनुसरण करने वाले कुछ अनुक्रमों को जोड़ते हैं (यह संख्याओं, कार्यों आदि का अनुक्रम हो सकता है)। सिस्टम से जुड़ी वस्तुओं की प्रकृति के आधार पर, ये संबंध बीजगणितीय, कार्यात्मक, विभेदक, अभिन्न आदि हो सकते हैं।

नायब. आर.एस. का प्रसिद्ध वर्ग आवर्ती कार्य है विशेष कार्य.इसके लिए हां बेलनाकार फलन Z m (x)पी। साथ। हमशक्ल

वे कार्य के अनुसार अनुमति देते हैं जेड एम0 (एक्स)फ़ंक्शंस ढूंढें Zm(x)पर टी= टी 0 बी 1, टी 0 बी 2आदि या, उदाहरण के लिए, फ़ंक्शन मानों द्वारा एक निश्चित बिंदु पर एक्स 0 . 0 (संख्यात्मक गणना में) किसी भी फ़ंक्शन का मान ज्ञात करें

उसी बिंदु पर (यहाँ) एम 0 - कोई भी वास्तविक संख्या)।

डॉ। आर.एस. का महत्वपूर्ण वर्ग। क्रमिक सन्निकटन की अनेक विधियाँ दीजिए (देखें)। पुनरावृत्ति विधि);यहां तरीके भी शामिल हैं. गड़बड़ी सिद्धांत.

क्वांटम यांत्रिकी में, एक अन्य प्रकार की गतिशील प्रणाली है जो राज्यों के हिल्बर्ट स्थान में वैक्टर को जोड़ती है। उदाहरण के लिए, स्थिर सामंजस्य ऑसिलेटर्स को गैर-नकारात्मक पूर्णांकों द्वारा मानकीकृत किया जाता है। संगत सदिश, द्वारा निरूपित, जहाँ एन- संपूर्ण, भिन्न के साथ एनसृजन संचालकों की कार्रवाई से एक दूसरे से प्राप्त किया जा सकता है एक +और विनाश ए:

इन संबंधों को किसी भी वेक्टर को (न्यूनतम ऊर्जा अवस्था) के रूप में व्यक्त करके हल किया जा सकता है। एच = 0):

इस निर्माण का एक सामान्यीकरण प्रतिनिधित्व है द्वितीयक परिमाणीकरणक्वांटम सांख्यिकी में यांत्रिकी और क्वांटम क्षेत्र सिद्धांत (देखें फोकाअंतरिक्ष)।

आर.एस. का एक विशिष्ट उदाहरण. सांख्यिकीय में यांत्रिकी - बोगोलीबॉव श्रृंखला बनाने वाले आंशिक वितरण कार्यों के समीकरण (देखें)। बोगोलीबॉव समीकरण);ऐसे कार्यों का ज्ञान आपको सभी थर्मोडायनामिक खोजने की अनुमति देता है। सिस्टम विशेषताएँ.

क्वांटम क्षेत्र सिद्धांत में, गतिशील उदाहरण के लिए, में निहित है ग्रीन के कार्य.उनकी गणना करने के लिए, विभिन्न का उपयोग करें। सन्निकटन, अक्सर - गड़बड़ी सिद्धांत का उपयोग कर गणना। एक वैकल्पिक दृष्टिकोण पूर्णांक-विभेदक पर आधारित है डायसन समीकरण,जो आर सिस्टम हैं: ग्रीन के दो-बिंदु फ़ंक्शन के समीकरण में चार-बिंदु फ़ंक्शन आदि शामिल हैं। बोगोल्युबोव के समीकरण की तरह, इस प्रणाली को केवल श्रृंखला को "तोड़ने" से हल किया जा सकता है ("ब्रेक" का स्थान आमतौर पर चुना जाता है) भौतिक विचारों से और यह निर्धारित करता है कि क्या प्राप्त किया गया है)।

एक अन्य प्रकार का आर. एस. क्वांटम क्षेत्र सिद्धांत में - भीड़ की अपनी पहचान होती हैसिद्धांतों में फ़ील्ड गेज करें.ये पहचान ग्रीन के कार्यों को विभिन्न कार्यों से जोड़ने वाले पूर्णांक-विभेदक संबंधों की एक श्रृंखला का भी प्रतिनिधित्व करती हैं। बाहरी रेखाओं की संख्या, पी सिद्धांत के गेज अपरिवर्तनीयता का परिणाम है। वे प्रक्रिया के दौरान गेज समरूपता की जांच करने में निर्णायक भूमिका निभाते हैं। पुनर्सामान्यीकरण.

अंततः, यह स्वयं भी एक आवर्ती प्रक्रिया है: प्रत्येक चरण पर (प्रत्येक बाद के लूप में) प्रतिसदस्य,कम लूप वाले आरेखों की गणना से प्राप्त किया गया (अधिक विवरण के लिए, देखें)। आर-ऑपरेशन)।ए. एम. मालोकोस्तोव।

भौतिक विश्वकोश. 5 खंडों में. - एम.: सोवियत विश्वकोश. प्रधान संपादक ए. एम. प्रोखोरोव. 1988 .

देखें अन्य शब्दकोशों में "आवर्ती संबंध" क्या हैं:

पुनरावृत्ति संबंध- - [एल.जी. सुमेंको। सूचना प्रौद्योगिकी पर अंग्रेजी-रूसी शब्दकोश। एम.: राज्य उद्यम TsNIIS, 2003.] विषय सूचान प्रौद्योगिकीसामान्य तौर पर एन पुनरावृत्ति संबंध... तकनीकी अनुवादक मार्गदर्शिका

- (वेबर फ़ंक्शंस) विशेष फ़ंक्शंस के लिए एक सामान्य नाम जो गणितीय भौतिकी के समीकरणों के लिए चर को अलग करने की विधि को लागू करके प्राप्त अंतर समीकरणों के समाधान हैं, जैसे लाप्लास समीकरण, समीकरण ... विकिपीडिया

या जोसेफस काउंटिंग राइम, ऐतिहासिक अर्थों वाली एक प्रसिद्ध गणितीय समस्या। यह कार्य उस किंवदंती पर आधारित है कि जोसेफस की टुकड़ी, योडफ़ैट शहर की रक्षा करते हुए, रोमनों की श्रेष्ठ सेनाओं के सामने आत्मसमर्पण नहीं करना चाहती थी जिन्होंने गुफा को अवरुद्ध कर दिया था... ...विकिपीडिया

पफनुति लवोविच चेबीशेव गणित में, ऑर्थोगोनल बहुपदों का एक क्रम वास्तविक बहुपदों का एक अनंत अनुक्रम है... विकिपीडिया

यह लेख हटाने के लिए प्रस्तावित है. कारणों की व्याख्या और संबंधित चर्चा विकिपीडिया पृष्ठ पर पाई जा सकती है: हटाया जाना है / 22 नवंबर, 2012। जबकि चर्चा प्रक्रिया है...विकिपीडिया

पाडोवन अनुक्रम एक पूर्णांक अनुक्रम P(n) है जिसमें प्रारंभिक मान और एक रैखिक पुनरावृत्ति संबंध है। P(n) के पहले मान 1, 1, 1, 2, 2, 3, 4, 5, 7 हैं , 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 ... विकिपीडिया

एक निश्चित प्रकार के हर्माइट बहुपद एक वास्तविक चर के बहुपदों का एक क्रम हैं। हर्माइट बहुपद संभाव्यता सिद्धांत, कॉम्बिनेटरिक्स और भौतिकी में उत्पन्न होते हैं। इन बहुपदों का नाम चार्ल्स हर्मिट के नाम पर रखा गया है। सामग्री 1... ...विकिपीडिया

- (बेसेल फ़ंक्शन) समाधान Zv(z) बेसेल समीकरण जहां पैरामीटर (सूचकांक) v एक मनमाना वास्तविक या जटिल संख्या है। अनुप्रयोगों में, चार मापदंडों पर निर्भर एक समीकरण अधिक बार सामने आता है: जिसके समाधान C के संदर्भ में व्यक्त किए जाते हैं... भौतिक विश्वकोश

रैखिक बीजगणितीय प्रणालियों की एक प्रणाली को हल करने की एक विधि। हर्मिटियन गैर-डीजेनरेट मैट्रिक्स ए के साथ समीकरण ए एक्स = बी। प्रत्यक्ष तरीकों के बीच, कंप्यूटर पर लागू होने पर यह सबसे प्रभावी है। विधि की कम्प्यूटेशनल योजना आम तौर पर हर्मिटियन फैक्टराइजेशन पर आधारित होती है... ... गणितीय विश्वकोश

संशोधित बेसेल फ़ंक्शन पूरी तरह से काल्पनिक तर्क के बेसेल फ़ंक्शन हैं। यदि बेसेल अंतर समीकरण में हम प्रतिस्थापित करते हैं, तो यह रूप ले लेगा इस समीकरण को संशोधित बेसेल समीकरण कहा जाता है ... विकिपीडिया