सबसे सरल त्रिकोणमितीय समीकरण समीकरण हैं

Cos(x)=a, पाप(x)=a, tg(x)=a, ctg(x)=a

समीकरण cos(x) = a

स्पष्टीकरण और तर्क

1. समीकरण cosx = a के मूल। कब | ए | > 1 समीकरण का कोई मूल नहीं है क्योंकि | कॉस्क्स |< 1 для любого x (прямая y = а при а >1 या ए पर< -1 не пересекает график функцииy = cosx).

चलो | ए |< 1. Тогда прямая у = а пересекает график функции

y = क्योंकि x. अंतराल पर, फलन y = cos x 1 से घटकर -1 हो जाता है। लेकिन एक घटता हुआ फ़ंक्शन अपने प्रत्येक मान को परिभाषा के क्षेत्र के केवल एक बिंदु पर लेता है, इसलिए समीकरण cos x \u003d a के इस अंतराल पर केवल एक जड़ है, जो आर्क कोसाइन की परिभाषा के अनुसार है: x 1 \u003d आर्ककोस ए (और इस रूट के लिए कॉस x \u003d ए)।

कोसाइन एक सम फलन है, अत: अंतराल पर [-p; 0] समीकरण cos x = और इसका केवल एक मूल है - x 1 के विपरीत संख्या, अर्थात

x 2 = -आर्ककोस ए.

इस प्रकार, अंतराल पर [-n; n] (लंबाई 2n) समीकरण cos x = a | के लिए ए |< 1 имеет только корни x = ±arccos а.

फ़ंक्शन y = cos x 2n की अवधि के साथ आवधिक है, इसलिए अन्य सभी जड़ें 2np (n € Z) द्वारा पाए गए जड़ों से भिन्न होती हैं। हमें समीकरण cos x = a कब के मूलों के लिए निम्नलिखित सूत्र प्राप्त होता है

x = ± आर्ककोस ए + 2 एन, एन £ जेड।

1. समीकरण cosx = a को हल करने के विशेष मामले।

समीकरण cos x = a के मूलों के लिए विशेष संकेतन को याद रखना उपयोगी है

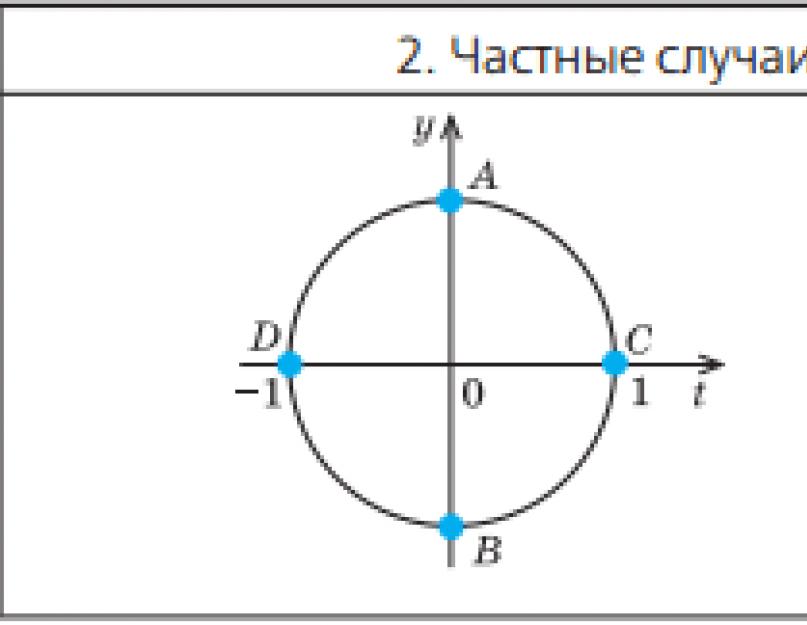
ए \u003d 0, ए \u003d -1, ए \u003d 1, जिसे गाइड के रूप में यूनिट सर्कल का उपयोग करके आसानी से प्राप्त किया जा सकता है।

चूँकि कोज्या इकाई वृत्त पर संगत बिंदु के भुज के बराबर है, हमें वह cos x = 0 मिलता है यदि और केवल यदि इकाई वृत्त पर संगत बिंदु बिंदु A या बिंदु B है।

इसी प्रकार, cos x = 1 यदि और केवल यदि इकाई वृत्त का संगत बिंदु बिंदु C है, इसलिए,

x = 2πp, k € Z.

इसके अलावा cos x = -1 यदि और केवल यदि इकाई वृत्त का संगत बिंदु बिंदु D है, तो x = n + 2n,

समीकरण पाप(x) = ए

स्पष्टीकरण और तर्क

1. समीकरण के मूल synx = a. कब | ए | > 1 समीकरण का कोई मूल नहीं है क्योंकि | सिनक्स |< 1 для любого x (прямая y = а на рисунке при а >1 या ए पर< -1 не пересекает график функции y = sinx).

त्रिकोणमितीय समीकरणों को हल करने की मुख्य विधियाँ हैं: समीकरणों को सरलतम बनाना (त्रिकोणमितीय सूत्रों का उपयोग करना), नए चर का परिचय देना, फैक्टरिंग करना। आइए उदाहरणों के साथ उनके अनुप्रयोग पर विचार करें। त्रिकोणमितीय समीकरणों के हल के पंजीकरण पर ध्यान दें।

त्रिकोणमितीय समीकरणों के सफल समाधान के लिए एक आवश्यक शर्त त्रिकोणमितीय सूत्रों (कार्य 6 का विषय 13) का ज्ञान है।

उदाहरण।

1. समीकरणों को सरलतम में घटाना।

1) समीकरण हल करें

समाधान:

उत्तर:

2) समीकरण के मूल ज्ञात कीजिए

(sinx + cosx) 2 = 1 - खंड से संबंधित synxcosx।

समाधान:

उत्तर:

2. द्विघात समीकरणों को कम करने वाले समीकरण।

1) समीकरण 2 पाप 2 x - cosx -1 = 0 को हल करें।

समाधान:सूत्र पाप 2 x \u003d 1 - cos 2 x का उपयोग करके, हम प्राप्त करते हैं

उत्तर:

2) समीकरण cos 2x = 1 + 4 cosx को हल करें।

समाधान:सूत्र cos 2x = 2 cos 2 x - 1 का उपयोग करने पर, हम पाते हैं

उत्तर:

3) समीकरण tgx - 2ctgx + 1 = 0 को हल करें

समाधान:

उत्तर:

3. सजातीय समीकरण

1) समीकरण 2sinx - 3cosx = 0 को हल करें

समाधान: मान लीजिए cosx = 0, तो 2sinx = 0 और synx = 0 - इस तथ्य के साथ एक विरोधाभास है कि पाप 2 x + cos 2 x = 1. तो cosx ≠ 0 और आप समीकरण को cosx से विभाजित कर सकते हैं। पाना

उत्तर:

2) समीकरण 1 + 7 cos 2 x = 3 syn 2x को हल करें

समाधान:

सूत्र 1 = पाप 2 x + cos 2 x और पाप 2x = 2 synxcosx का उपयोग करके, हम पाते हैं

syn2x + cos2x + 7cos2x = 6sinxcosx
पाप2x - 6sinxcosx+ 8cos2x = 0

मान लीजिए कि cosx = 0 है, तो पाप 2 x = 0 और पापx = 0 - इस तथ्य के साथ विरोधाभास है कि पाप 2 x + cos 2 x = 1।
तो cosx ≠ 0 और हम समीकरण को cos 2 x से विभाजित कर सकते हैं . पाना

टीजी 2एक्स - 6 टीजीएक्स + 8 = 0
tgx = y को निरूपित करें
y 2 – 6 y + 8 = 0
y 1 = 4; y2=2
ए) टीजीएक्स = 4, एक्स= आर्कटीजी4 + 2 क, क
बी) टीजीएक्स = 2, एक्स= आर्कटीजी2 + 2 क, क .

उत्तर:आर्कटजी4 + 2 क, आर्कटैन2 + 2 के, के

4. रूप के समीकरण एसिनक्स + बी cosx = साथ साथ≠ 0.

1) समीकरण हल करें.

समाधान:

उत्तर:

5. गुणनखंडन द्वारा हल किये गये समीकरण।

1) समीकरण पाप2x - पापx = 0 को हल करें।

समीकरण की जड़ एफ (एक्स) = φ ( एक्स) केवल संख्या 0 के रूप में कार्य कर सकता है। आइए इसे जांचें:

क्योंकि 0 = 0 + 1 - समानता सत्य है।

संख्या 0 इस समीकरण का एकमात्र मूल है।

उत्तर: 0.

आप अपनी समस्या का विस्तृत समाधान ऑर्डर कर सकते हैं!!!

एक त्रिकोणमितीय फलन (`sin x, cos x, tg x` या `ctg x`) के चिह्न के नीचे एक अज्ञात युक्त समानता को त्रिकोणमितीय समीकरण कहा जाता है, और हम उनके सूत्रों पर आगे विचार करेंगे।

सबसे सरल समीकरण हैं `sin x=a, cos x=a, tg x=a, ctg x=a`, जहां `x` पाया जाने वाला कोण है, `a` कोई संख्या है। आइए उनमें से प्रत्येक के लिए मूल सूत्र लिखें।

1. समीकरण `sin x=a`.

`|a|>1` के लिए इसका कोई समाधान नहीं है।

`|ए| के साथ \leq 1` में अनंत संख्या में समाधान हैं।

मूल सूत्र: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. समीकरण `cos x=a`

`|a|>1` के लिए - जैसा कि साइन के मामले में होता है, वास्तविक संख्याओं के बीच कोई समाधान नहीं होता है।

`|ए| के साथ \leq 1` में अनंत संख्या में समाधान हैं।

मूल सूत्र: `x=\pm arccos a + 2\pi n, n \in Z`

ग्राफ़ में साइन और कोसाइन के लिए विशेष मामले।

3. समीकरण `tg x=a`

`a` के किसी भी मान के लिए अनंत संख्या में समाधान हैं।

मूल सूत्र: `x=arctg a + \pi n, n \in Z`

4. समीकरण `ctg x=a`

इसमें `ए` के किसी भी मान के लिए अनंत संख्या में समाधान भी हैं।

मूल सूत्र: `x=arcctg a + \pi n, n \in Z`

तालिका में त्रिकोणमितीय समीकरणों की जड़ों के लिए सूत्र

साइनस के लिए:
कोसाइन के लिए:
स्पर्शरेखा और कोटैंजेंट के लिए:
व्युत्क्रम त्रिकोणमितीय फलन वाले समीकरणों को हल करने के सूत्र:

त्रिकोणमितीय समीकरणों को हल करने की विधियाँ

किसी भी त्रिकोणमितीय समीकरण के समाधान में दो चरण होते हैं:

• इसे सरलतम में बदलने के लिए उपयोग करना;
• मूलों और तालिकाओं के लिए उपरोक्त सूत्रों का उपयोग करके परिणामी सरल समीकरण को हल करें।

आइए उदाहरणों का उपयोग करके समाधान के मुख्य तरीकों पर विचार करें।

बीजगणितीय विधि.

इस विधि में किसी चर का प्रतिस्थापन तथा उसका समानता में प्रतिस्थापन किया जाता है।

उदाहरण। समीकरण को हल करें: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,

प्रतिस्थापन करें: `cos(x+\frac \pi 6)=y`, फिर `2y^2-3y+1=0`,

हम मूल पाते हैं: `y_1=1, y_2=1/2`, जिससे दो मामले आते हैं:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

उत्तर: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`।

गुणनखंडीकरण।

उदाहरण। समीकरण हल करें: `sin x+cos x=1`.

समाधान। समानता के सभी पदों को बाईं ओर ले जाएँ: `sin x+cos x-1=0`। का उपयोग करते हुए, हम बाईं ओर को रूपांतरित और गुणनखंडित करते हैं:

`sin x - 2sin^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sin x/2 (cos x/2-sin x/2)=0`,

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.

उत्तर: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

एक सजातीय समीकरण में कमी

सबसे पहले, आपको इस त्रिकोणमितीय समीकरण को दो रूपों में से एक में लाना होगा:

`a syn x+b cos x=0` (पहली डिग्री का सजातीय समीकरण) या `a syn^2 x + b syn x cos x +c cos^2 x=0` (दूसरी डिग्री का सजातीय समीकरण)।

फिर पहले मामले के लिए दोनों भागों को `cos x \ne 0` से विभाजित करें, और दूसरे के लिए `cos^2 x \ne 0` से विभाजित करें। हमें `tg x` के लिए समीकरण मिलते हैं: `a tg x+b=0` और `a tg^2 x + b tg x +c =0`, जिन्हें ज्ञात तरीकों का उपयोग करके हल किया जाना चाहिए।

उदाहरण। समीकरण हल करें: `2sin^2 x+sin x cos x - cos^2 x=1`.

समाधान। आइए दाएँ पक्ष को `1=sin^2 x+cos^2 x` के रूप में लिखें:

`2 पाप^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 पाप^2 x+sin x cos x - cos^2 x -` ` पाप^2 x - cos^2 x=0`

`sin^2 x+sin x cos x - 2 cos^2 x=0`.

यह दूसरी डिग्री का एक सजातीय त्रिकोणमितीय समीकरण है, इसके बाएँ और दाएँ पक्षों को `cos^2 x \ne 0` से विभाजित करने पर, हमें मिलता है:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) - \frac(2 cos^2 x)(cos^2 x)=0`

`tg^2 x+tg x - 2=0`. आइए प्रतिस्थापन `tg x=t` का परिचय दें, जिसके परिणामस्वरूप `t^2 + t - 2=0` होता है। इस समीकरण की जड़ें `t_1=-2` और `t_2=1` हैं। तब:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`।

उत्तर। `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.

हाफ कॉर्नर पर जाएं

उदाहरण। समीकरण हल करें: `11 पाप x - 2 cos x = 10`।

समाधान। दोहरे कोण सूत्रों को लागू करने पर, परिणाम है: `22 पाप (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 पाप^2 x/2=` `10 पाप^2 x /2 +10 cos^2 x/2`

`4 tg^2 x/2 - 11 tg x/2 +6=0`

ऊपर वर्णित बीजगणितीय विधि को लागू करने पर, हम प्राप्त करते हैं:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
2. `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`।

उत्तर। `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`।

एक सहायक कोण का परिचय

त्रिकोणमितीय समीकरण `a syn x + b cos x =c` में, जहां a,b,c गुणांक हैं और x एक चर है, हम दोनों भागों को `sqrt (a^2+b^2)` से विभाजित करते हैं:

`\frac a(sqrt (a^2+b^2)) syn x +` `\frac b(sqrt (a^2+b^2)) cos x =`\frac c(sqrt (a^2) +बी^2))`.

बाईं ओर के गुणांकों में साइन और कोसाइन के गुण हैं, अर्थात्, उनके वर्गों का योग 1 के बराबर है और उनका मापांक 1 से अधिक नहीं है। उन्हें निम्नानुसार निरूपित करें: `\frac a(sqrt (a^2+) b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2))= सी`, फिर:

`cos \varphi पाप x + पाप \varphi cos x =C`।

आइए निम्नलिखित उदाहरण पर करीब से नज़र डालें:

उदाहरण। समीकरण हल करें: `3sin x+4 cos x=2`.

समाधान। समीकरण के दोनों पक्षों को `sqrt (3^2+4^2)` ​​से विभाजित करने पर, हमें मिलता है:

`\frac (3 पाप x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))`

`3/5 पाप x+4/5 cos x=2/5`.

`3/5 = cos \varphi` , `4/5=sin \varphi` को निरूपित करें। चूँकि `sin \varphi>0`, `cos \varphi>0`, हम `\varphi=arcsin 4/5` को सहायक कोण के रूप में लेते हैं। फिर हम अपनी समानता को इस रूप में लिखते हैं:

`cos \varphi syn x+sin \varphi cos x=2/5`

ज्या के कोणों के योग के सूत्र को लागू करते हुए, हम अपनी समानता को निम्नलिखित रूप में लिखते हैं:

`sin(x+\varphi)=2/5`,

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

उत्तर। `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

भिन्नात्मक-तर्कसंगत त्रिकोणमितीय समीकरण

ये भिन्नों के साथ समानताएं हैं, जिनके अंश और हर में त्रिकोणमितीय कार्य होते हैं।

उदाहरण। प्रश्न हल करें। `\frac (sin x)(1+cos x)=1-cos x`.

समाधान। समीकरण के दाएँ पक्ष को `(1+cos x)` से गुणा और विभाजित करें। परिणामस्वरूप, हमें मिलता है:

`\frac ((sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=`\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`

`\frac (sin x-sin^2 x)(1+cos x)=0`

यह देखते हुए कि हर शून्य नहीं हो सकता, हमें `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z` मिलता है।

भिन्न के अंश को शून्य के बराबर करें: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. फिर `sin x=0` या `1-sin x=0`.

1. `sin x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`।

यह देखते हुए कि ` x \ne \pi+2\pi n, n \in Z`, समाधान हैं `x=2\pi n, n \in Z` और `x=\pi /2+2\pi n` , `n \in Z`.

उत्तर। `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`।

त्रिकोणमिति, और विशेष रूप से त्रिकोणमितीय समीकरण, ज्यामिति, भौतिकी और इंजीनियरिंग के लगभग सभी क्षेत्रों में उपयोग किए जाते हैं। अध्ययन 10वीं कक्षा में शुरू होता है, परीक्षा के लिए हमेशा कार्य होते हैं, इसलिए त्रिकोणमितीय समीकरणों के सभी सूत्रों को याद करने का प्रयास करें - वे निश्चित रूप से आपके काम आएंगे!

हालाँकि, आपको उन्हें याद रखने की भी आवश्यकता नहीं है, मुख्य बात सार को समझना और निष्कर्ष निकालने में सक्षम होना है। यह उतना कठिन नहीं है जितना लगता है। वीडियो देखकर आप खुद ही देख लीजिए.

वीडियो पाठ्यक्रम "गेट एन ए" में गणित में 60-65 अंकों से परीक्षा में सफल उत्तीर्ण होने के लिए आवश्यक सभी विषय शामिल हैं। प्रोफ़ाइल के सभी कार्य 1-13 गणित में उपयोग करें। गणित में बेसिक यूएसई पास करने के लिए भी उपयुक्त। यदि आप 90-100 अंकों के साथ परीक्षा उत्तीर्ण करना चाहते हैं, तो आपको भाग 1 को 30 मिनट में और गलतियों के बिना हल करना होगा!

कक्षा 10-11 के साथ-साथ शिक्षकों के लिए परीक्षा की तैयारी का पाठ्यक्रम। गणित में परीक्षा के भाग 1 (पहली 12 समस्याएं) और समस्या 13 (त्रिकोणमिति) को हल करने के लिए आपको जो कुछ भी चाहिए वह सब कुछ। और यह एकीकृत राज्य परीक्षा में 70 अंक से अधिक है, और न तो सौ अंक वाला छात्र और न ही कोई मानवतावादी इनके बिना रह सकता है।

सभी आवश्यक सिद्धांत. त्वरित तरीकेपरीक्षा के समाधान, जाल और रहस्य। FIPI कार्यों के बैंक से भाग 1 के सभी प्रासंगिक कार्यों का विश्लेषण किया गया है। पाठ्यक्रम पूरी तरह से USE-2018 की आवश्यकताओं का अनुपालन करता है।

पाठ्यक्रम में 5 बड़े विषय हैं, प्रत्येक विषय 2.5 घंटे का है। प्रत्येक विषय प्रारंभ से, सरल और स्पष्ट रूप से दिया गया है।

सैकड़ों परीक्षा कार्य। पाठ समस्याएँ और संभाव्यता सिद्धांत। समस्या समाधान एल्गोरिदम को याद रखना सरल और आसान है। ज्यामिति. सिद्धांत, संदर्भ सामग्री, सभी प्रकार के यूएसई कार्यों का विश्लेषण। स्टीरियोमेट्री। हल करने के लिए चालाक तरकीबें, उपयोगी चीट शीट, स्थानिक कल्पना का विकास। खरोंच से त्रिकोणमिति - कार्य 13 तक। रटने के बजाय समझना। जटिल अवधारणाओं की दृश्य व्याख्या. बीजगणित. मूल, घात और लघुगणक, कार्य और व्युत्पन्न। परीक्षा के दूसरे भाग की जटिल समस्याओं को हल करने का आधार।

आपकी निजता हमारे लिए महत्वपूर्ण है। इस कारण से, हमने एक गोपनीयता नीति विकसित की है जो बताती है कि हम आपकी जानकारी का उपयोग और भंडारण कैसे करते हैं। कृपया हमारी गोपनीयता नीति पढ़ें और यदि आपके कोई प्रश्न हों तो हमें बताएं।

व्यक्तिगत जानकारी का संग्रहण एवं उपयोग

व्यक्तिगत जानकारी से तात्पर्य उस डेटा से है जिसका उपयोग किसी विशिष्ट व्यक्ति की पहचान करने या उससे संपर्क करने के लिए किया जा सकता है।

जब भी आप हमसे संपर्क करेंगे तो आपसे किसी भी समय आपकी व्यक्तिगत जानकारी प्रदान करने के लिए कहा जा सकता है।

निम्नलिखित कुछ उदाहरण हैं कि हम किस प्रकार की व्यक्तिगत जानकारी एकत्र कर सकते हैं और हम ऐसी जानकारी का उपयोग कैसे कर सकते हैं।

हम कौन सी व्यक्तिगत जानकारी एकत्र करते हैं:

• जब आप साइट पर कोई आवेदन जमा करते हैं, तो हम आपका नाम, फ़ोन नंबर, ईमेल पता आदि सहित विभिन्न जानकारी एकत्र कर सकते हैं।

हम आपकी व्यक्तिगत जानकारी का उपयोग कैसे करते हैं:

• हमारे द्वारा एकत्र की गई व्यक्तिगत जानकारी हमें आपसे संपर्क करने और आपको अद्वितीय प्रस्तावों, प्रचारों और अन्य घटनाओं और आगामी घटनाओं के बारे में सूचित करने की अनुमति देती है।
• समय-समय पर, हम आपको महत्वपूर्ण सूचनाएं और संचार भेजने के लिए आपकी व्यक्तिगत जानकारी का उपयोग कर सकते हैं।
• हम व्यक्तिगत जानकारी का उपयोग आंतरिक उद्देश्यों के लिए भी कर सकते हैं, जैसे कि हमारे द्वारा प्रदान की जाने वाली सेवाओं को बेहतर बनाने और आपको हमारी सेवाओं के संबंध में सिफारिशें प्रदान करने के लिए ऑडिट, डेटा विश्लेषण और विभिन्न शोध करना।
• यदि आप किसी पुरस्कार ड्रा, प्रतियोगिता या इसी तरह के प्रोत्साहन में भाग लेते हैं, तो हम आपके द्वारा प्रदान की गई जानकारी का उपयोग ऐसे कार्यक्रमों को संचालित करने के लिए कर सकते हैं।

तीसरे पक्ष को प्रकटीकरण

हम आपसे प्राप्त जानकारी को तीसरे पक्ष को प्रकट नहीं करते हैं।

अपवाद:

• इस घटना में कि यह आवश्यक है - कानून के अनुसार, न्यायिक आदेश, कानूनी कार्यवाही में, और / या सार्वजनिक अनुरोधों या रूसी संघ के क्षेत्र में राज्य निकायों के अनुरोधों के आधार पर - अपनी व्यक्तिगत जानकारी का खुलासा करें। यदि हम यह निर्धारित करते हैं कि ऐसा प्रकटीकरण सुरक्षा, कानून प्रवर्तन, या अन्य सार्वजनिक हित उद्देश्यों के लिए आवश्यक या उचित है, तो हम आपके बारे में जानकारी का खुलासा भी कर सकते हैं।
• पुनर्गठन, विलय या बिक्री की स्थिति में, हम एकत्र की गई व्यक्तिगत जानकारी को संबंधित तीसरे पक्ष के उत्तराधिकारी को हस्तांतरित कर सकते हैं।

व्यक्तिगत जानकारी की सुरक्षा

हम आपकी व्यक्तिगत जानकारी को हानि, चोरी और दुरुपयोग के साथ-साथ अनधिकृत पहुंच, प्रकटीकरण, परिवर्तन और विनाश से बचाने के लिए - प्रशासनिक, तकनीकी और भौतिक सहित - सावधानियां बरतते हैं।

कंपनी स्तर पर अपनी गोपनीयता बनाए रखना

यह सुनिश्चित करने के लिए कि आपकी व्यक्तिगत जानकारी सुरक्षित है, हम अपने कर्मचारियों को गोपनीयता और सुरक्षा प्रथाओं के बारे में बताते हैं और गोपनीयता प्रथाओं को सख्ती से लागू करते हैं।