Najprostsze równania trygonometryczne to równania

Cos(x)=a, sin(x)=a, tg(x)=a, ctg(x)=a

Równanie cos(x) = a

Wyjaśnienie i uzasadnienie

1. Pierwiastki równania cosx = a. Kiedy | | > 1 równanie nie ma pierwiastków, ponieważ | cosx |< 1 для любого x (прямая y = а при а >1 lub o godz< -1 не пересекает график функцииy = cosx).

Niech | |< 1. Тогда прямая у = а пересекает график функции

y = cos x. W przedziale funkcja y = cos x zmniejsza się od 1 do -1. Ale funkcja malejąca przyjmuje każdą ze swoich wartości tylko w jednym punkcie swojej dziedziny definicji, dlatego równanie cos x = a ma tylko jeden pierwiastek na tym przedziale, który z definicji łuku cosinusa wynosi: x 1 = arccos a (i dla tego pierwiastka cos x = a).

Cosinus jest funkcją parzystą, więc na przedziale [-n; 0] równanie cos x = a także ma tylko jeden pierwiastek - liczbę przeciwną do x 1, czyli

x 2 = - arccos a.

Tak więc w przedziale [-n; n] (długość 2n) równanie cos x = a dla | |< 1 имеет только корни x = ±arccos а.

Funkcja y = cos x jest okresowa z okresem 2n, więc wszystkie inne pierwiastki różnią się od tych znalezionych przez 2np (n € Z). Otrzymujemy następujący wzór na pierwiastki równania cos x = i kiedy

x = ± arccos a + 2n, n £ Z.

1. Szczególne przypadki rozwiązania równania cosx = a.

Warto pamiętać o specjalnej notacji pierwiastków równania cos x = a when

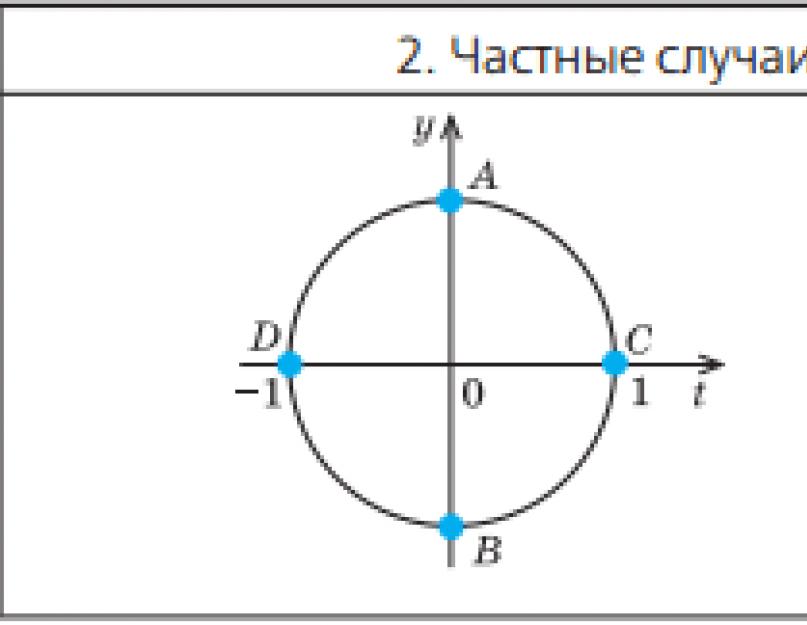
a \u003d 0, a \u003d -1, a \u003d 1, które można łatwo uzyskać, używając okręgu jednostkowego jako przewodnika.

Ponieważ cosinus jest równy odciętej odpowiedniego punktu na okręgu jednostkowym, otrzymujemy, że cos x = 0 wtedy i tylko wtedy, gdy odpowiadający punkt na okręgu jednostkowym jest punktem A lub punktem B.

Podobnie, cos x = 1 wtedy i tylko wtedy, gdy odpowiednim punktem okręgu jednostkowego jest punkt C, zatem

x = 2πp, k € Z.

Również cos x \u003d -1 wtedy i tylko wtedy, gdy odpowiednim punktem okręgu jednostkowego jest punkt D, a zatem x \u003d n + 2n,

Równanie sin(x) = a

Wyjaśnienie i uzasadnienie

1. Pierwiastki równania sinx = a. Kiedy | | > 1 równanie nie ma pierwiastków, ponieważ | sinx |< 1 для любого x (прямая y = а на рисунке при а >1 lub o godz< -1 не пересекает график функции y = sinx).

Główne metody rozwiązywania równań trygonometrycznych to: sprowadzanie równań do najprostszych (przy użyciu formuł trygonometrycznych), wprowadzanie nowych zmiennych oraz faktoring. Rozważmy ich zastosowanie na przykładach. Zwróć uwagę na projekt rozwiązania równań trygonometrycznych.

Warunkiem koniecznym do pomyślnego rozwiązania równań trygonometrycznych jest znajomość wzorów trygonometrycznych (temat 13 pracy 6).

Przykłady.

1. Równania redukujące do najprostszego.

1) Rozwiąż równanie

Rozwiązanie:

Odpowiadać:

2) Znajdź pierwiastki równania

(sinx + cosx) 2 = 1 – sinxcosx należący do segmentu .

Rozwiązanie:

Odpowiadać:

2. Równania redukujące do równań kwadratowych.

1) Rozwiąż równanie 2 sin 2 x - cosx -1 = 0.

Rozwiązanie: Używając wzoru sin 2 x \u003d 1 - cos 2 x, otrzymujemy

Odpowiadać:

2) Rozwiąż równanie cos 2x = 1 + 4 cosx.

Rozwiązanie: Korzystając ze wzoru cos 2x = 2 cos 2 x - 1, otrzymujemy

Odpowiadać:

3) Rozwiąż równanie tgx - 2ctgx + 1 = 0

Rozwiązanie:

Odpowiadać:

3. Równania jednorodne

1) Rozwiąż równanie 2sinx - 3cosx = 0

Rozwiązanie: Niech cosx = 0, potem 2sinx = 0 i sinx = 0 - sprzeczność z tym, że sin 2 x + cos 2 x = 1. Czyli cosx ≠ 0 i równanie można podzielić przez cosx. Dostać

Odpowiadać:

2) Rozwiąż równanie 1 + 7 cos 2 x = 3 sin 2x

Rozwiązanie:

Używając wzorów 1 = sin 2 x + cos 2 x i sin 2x = 2 sinxcosx, otrzymujemy

sin2x + cos2x + 7cos2x = 6sinxcosx
sin2x - 6sinxcosx+ 8cos2x = 0

Niech cosx = 0, potem sin 2 x = 0 i sinx = 0 - sprzeczność z tym, że sin 2 x + cos 2 x = 1.
Czyli cosx ≠ 0 i możemy podzielić równanie przez cos 2 x . Dostać

tg 2x – 6 tgx + 8 = 0
Oznacz tgx = y
r 2 – 6 r + 8 = 0
y1 = 4; y2=2
a) tanx = 4, x= arctg4 + 2 k, k
b) tgx = 2, x= arctg2 + 2 k, k .

Odpowiadać: arctg4 + 2 k, arctan2 + 2 k, k

4. Równania postaci a sinx + b cosx = z, z≠ 0.

1) Rozwiąż równanie.

Rozwiązanie:

Odpowiadać:

5. Równania rozwiązane przez faktoryzację.

1) Rozwiąż równanie sin2x - sinx = 0.

Pierwiastek równania f (X) = φ ( X) może służyć tylko jako liczba 0. Sprawdźmy to:

cos 0 = 0 + 1 - równość jest prawdziwa.

Liczba 0 jest jedynym pierwiastkiem tego równania.

Odpowiadać: 0.

Możesz zamówić szczegółowe rozwiązanie swojego problemu !!!

Równość zawierająca niewiadomą pod znakiem funkcji trygonometrycznej (`sin x, cos x, tg x` lub `ctg x`) nazywa się równaniem trygonometrycznym, a ich wzory rozważymy dalej.

Najprostsze równania to `sin x=a, cos x=a, tg x=a, ctg x=a`, gdzie `x` jest kątem do znalezienia, `a` jest dowolną liczbą. Napiszmy dla każdego z nich formuły pierwiastkowe.

1. Równanie „sin x=a”.

Dla `|a|>1` nie ma rozwiązań.

Z `|a| \leq 1` ma nieskończoną liczbę rozwiązań.

Wzór na pierwiastek: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Równanie `cos x=a`

Dla `|a|>1` - jak w przypadku sinusa, nie ma rozwiązań wśród liczb rzeczywistych.

Z `|a| \leq 1` ma nieskończoną liczbę rozwiązań.

Wzór pierwiastka: `x=\pm arccos a + 2\pi n, n \in Z`

Szczególne przypadki dla sinusa i cosinusa w wykresach.

3. Równanie `tg x=a`

Ma nieskończoną liczbę rozwiązań dla dowolnych wartości „a”.

Wzór na pierwiastek: `x=arctg a + \pi n, n \in Z`

4. Równanie `ctg x=a`

Posiada również nieskończoną ilość rozwiązań dla dowolnych wartości „a”.

Wzór na pierwiastek: `x=arcctg a + \pi n, n \in Z`

Wzory na pierwiastki równań trygonometrycznych w tabeli

Zatok:
Dla cosinusa:
Dla stycznej i cotangensa:
Wzory do rozwiązywania równań zawierających odwrotne funkcje trygonometryczne:

Metody rozwiązywania równań trygonometrycznych

Rozwiązanie dowolnego równania trygonometrycznego składa się z dwóch etapów:

• za pomocą przekonwertować go na najprostszy;
• rozwiąż powstałe proste równanie, korzystając z powyższych wzorów dla pierwiastków i tabel.

Rozważmy główne metody rozwiązania na przykładach.

metoda algebraiczna.

W tej metodzie dokonuje się zamiany zmiennej i jej podstawienia na równość.

Przykład. Rozwiąż równanie: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,

dokonaj zamiany: `cos(x+\frac \pi 6)=y`, następnie `2y^2-3y+1=0`,

znajdujemy pierwiastki: `y_1=1, y_2=1/2`, z których wynikają dwa przypadki:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Odpowiedź: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Faktoryzacja.

Przykład. Rozwiąż równanie: `sin x+cos x=1`.

Rozwiązanie. Przesuń w lewo wszystkie warunki równości: `sin x+cos x-1=0`. Używając , przekształcamy i rozkładamy na czynniki lewą stronę:

`sin x - 2sin^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sin x/2 (cos x/2-sin x/2)=0`,

1. `sin x/2 =0`, `x/2=\pi n`, `x_1=2\pi n`.
2. `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.

Odpowiedź: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Redukcja do równania jednorodnego

Najpierw musisz sprowadzić to równanie trygonometryczne do jednej z dwóch postaci:

`a sin x+b cos x=0` (jednorodne równanie pierwszego stopnia) lub `a sin^2 x + b sin x cos x +c cos^2 x=0` (jednorodne równanie drugiego stopnia).

Następnie podziel obie części przez `cos x \ne 0` dla pierwszego przypadku i przez `cos^2 x \ne 0` dla drugiego. Otrzymujemy równania dla `tg x`: `a tg x+b=0` oraz `a tg^2 x + b tg x +c =0`, które należy rozwiązać znanymi metodami.

Przykład. Rozwiąż równanie: `2 sin^2 x+sin x cos x - cos^2 x=1`.

Rozwiązanie. Zapiszmy prawą stronę jako `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x - cos^2 x -` ` sin^2 x - cos^2 x=0`

`sin^2 x+sin x cos x - 2 cos^2 x=0`.

Jest to jednorodne równanie trygonometryczne drugiego stopnia, dzieląc jego lewą i prawą stronę przez `cos^2 x \ne 0`, otrzymujemy:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) - \frac(2 cos^2 x)(cos^2 x)=0`

`tg^2 x+tg x - 2=0`. Wprowadźmy zamiennik `tg x=t`, w wyniku czego `t^2 + t - 2=0`. Pierwiastki tego równania to „t_1=-2” i „t_2=1”. Następnie:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \w Z`.

Odpowiadać. `x_1=arctg (-2)+\pi n`, `n \w Z`, `x_2=\pi/4+\pi n`, `n \w Z`.

Przejdź do połowy rogu

Przykład. Rozwiąż równanie: `11 sin x - 2 cos x = 10`.

Rozwiązanie. Stosując formuły podwójnego kąta, wynik jest następujący: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`

`4 tg^2 x/2 - 11 tg x/2 +6=0`

Stosując opisaną powyżej metodę algebraiczną otrzymujemy:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
2. `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Odpowiadać. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Wprowadzenie kąta pomocniczego

W równaniu trygonometrycznym `a sin x + b cos x =c`, gdzie a,b,c są współczynnikami, a x jest zmienną, dzielimy obie części przez `sqrt (a^2+b^2)`:

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2 +b^2))".

Współczynniki po lewej stronie mają właściwości sinusa i cosinusa, a mianowicie suma ich kwadratów wynosi 1, a ich moduł wynosi co najwyżej 1. Oznaczmy je następująco: `\frac a(sqrt (a^2+b^ 2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2))=C` , następnie:

`cos \varphi sin x + sin \varphi cos x =C`.

Przyjrzyjmy się bliżej następującemu przykładowi:

Przykład. Rozwiąż równanie: `3 sin x+4 cos x=2`.

Rozwiązanie. Dzieląc obie strony równania przez `sqrt (3^2+4^2)` ​​otrzymujemy:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))`

`3/5 sin x+4/5 cos x=2/5`.

Oznaczmy `3/5 = cos \varphi` , `4/5=sin \varphi`. Ponieważ `sin \varphi>0`, `cos \varphi>0` przyjmujemy `\varphi=arcsin 4/5` jako kąt pomocniczy. Następnie zapisujemy naszą równość w postaci:

`cos \varphi sin x+sin \varphi cos x=2/5`

Stosując wzór na sumę kątów dla sinusa, zapisujemy naszą równość w postaci:

`sin(x+\varphi)=2/5`,

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcsw 2/5-` `arcsin 4/5+ \pi n`, `n \w Z`.

Odpowiadać. `x=(-1)^n arcsw 2/5-` `arcsin 4/5+ \pi n`, `n \w Z`.

Ułamkowo-racjonalne równania trygonometryczne

Są to równości z ułamkami, w których licznikach i mianownikach znajdują się funkcje trygonometryczne.

Przykład. Rozwiązać równanie. `\frac (sin x)(1+cos x)=1-cos x`.

Rozwiązanie. Pomnóż i podziel prawą stronę równania przez `(1+cos x)`. W rezultacie otrzymujemy:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`

`\frac (sin x-sin^2 x)(1+cos x)=0`

Biorąc pod uwagę, że mianownik nie może wynosić zero, otrzymujemy `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.

Przyrównaj licznik ułamka do zera: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Następnie „sin x=0” lub „1-sin x=0”.

1. `sin x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

Biorąc pod uwagę, że ` x \ne \pi+2\pi n, n \in Z`, rozwiązaniami są `x=2\pi n, n \in Z` i `x=\pi /2+2\pi n` , `n \w Z`.

Odpowiadać. `x=2\pi n`, `n \w Z`, `x=\pi /2+2\pi n`, `n \w Z`.

Trygonometria, aw szczególności równania trygonometryczne, są używane w prawie wszystkich dziedzinach geometrii, fizyki i inżynierii. Nauka zaczyna się w 10 klasie, zawsze są zadania do egzaminu, więc postaraj się zapamiętać wszystkie wzory równań trygonometrycznych - na pewno Ci się przydadzą!

Jednak nie musisz ich nawet zapamiętywać, najważniejsze jest zrozumienie istoty i umiejętność wywnioskowania. Nie jest to takie trudne, jak się wydaje. Przekonaj się sam, oglądając wideo.

Kurs wideo „Get an A” zawiera wszystkie tematy niezbędne do pomyślnego zdania egzaminu z matematyki o 60-65 punktów. Całkowicie wszystkie zadania 1-13 z profilu USE w matematyce. Nadaje się również do zaliczenia podstawowego USE w matematyce. Jeśli chcesz zdać egzamin na 90-100 punktów, musisz rozwiązać część 1 w 30 minut i bez błędów!

Kurs przygotowujący do egzaminu dla klas 10-11, a także dla nauczycieli. Wszystko, czego potrzebujesz do rozwiązania części 1 egzaminu z matematyki (12 pierwszych zadań) i zadania 13 (trygonometria). A to ponad 70 punktów na Zjednoczonym Egzaminu Państwowym i ani stupunktowy student, ani humanista nie mogą się bez nich obejść.

Cała niezbędna teoria. Szybkie rozwiązania, pułapki i tajemnice egzaminu. Przeanalizowano wszystkie istotne zadania części 1 z zadań Banku FIPI. Kurs w pełni zgodny z wymaganiami USE-2018.

Kurs zawiera 5 dużych tematów po 2,5 godziny każdy. Każdy temat podany jest od podstaw, prosto i przejrzyście.

Setki zadań egzaminacyjnych. Problemy tekstowe i teoria prawdopodobieństwa. Proste i łatwe do zapamiętania algorytmy rozwiązywania problemów. Geometria. Teoria, materiał referencyjny, analiza wszystkich typów zadań USE. Stereometria. Sprytne sztuczki do rozwiązywania, przydatne ściągawki, rozwijanie wyobraźni przestrzennej. Trygonometria od podstaw - do zadania 13. Zrozumienie zamiast wkuwania. Wizualne wyjaśnienie złożonych pojęć. Algebra. Pierwiastki, potęgi i logarytmy, funkcja i pochodna. Baza do rozwiązywania złożonych problemów II części egzaminu.

Twoja prywatność jest dla nas ważna. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Przeczytaj naszą politykę prywatności i daj nam znać, jeśli masz jakiekolwiek pytania.

Gromadzenie i wykorzystywanie danych osobowych

Dane osobowe to dane, które można wykorzystać do zidentyfikowania konkretnej osoby lub skontaktowania się z nią.

Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie, gdy się z nami skontaktujesz.

Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić oraz sposobu, w jaki możemy je wykorzystywać.

Jakie dane osobowe zbieramy:

• Kiedy przesyłasz wniosek na stronie, możemy zbierać różne informacje, w tym imię i nazwisko, numer telefonu, adres e-mail itp.

Jak wykorzystujemy Twoje dane osobowe:

• Gromadzone przez nas dane osobowe pozwalają nam kontaktować się z Tobą i informować Cię o wyjątkowych ofertach, promocjach i innych wydarzeniach oraz nadchodzących wydarzeniach.
• Od czasu do czasu możemy wykorzystywać Twoje dane osobowe, aby wysyłać Ci ważne powiadomienia i komunikaty.
• Możemy również wykorzystywać dane osobowe do celów wewnętrznych, takich jak przeprowadzanie audytów, analiza danych i różne badania w celu ulepszenia świadczonych przez nas usług i udzielania rekomendacji dotyczących naszych usług.
• Jeśli weźmiesz udział w losowaniu nagród, konkursie lub podobnym programie motywacyjnym, możemy wykorzystać podane przez Ciebie informacje do administrowania takimi programami.

Ujawnianie osobom trzecim

Nie ujawniamy informacji otrzymanych od Ciebie stronom trzecim.

Wyjątki:

• W przypadku, gdy jest to konieczne - zgodnie z prawem, nakazem sądowym, w postępowaniu sądowym i / lub na podstawie publicznych żądań lub wniosków organów państwowych na terytorium Federacji Rosyjskiej - ujawnij swoje dane osobowe. Możemy również ujawnić informacje o Tobie, jeśli uznamy, że takie ujawnienie jest konieczne lub odpowiednie ze względów bezpieczeństwa, egzekwowania prawa lub z innych względów interesu publicznego.
• W przypadku reorganizacji, fuzji lub sprzedaży możemy przekazać zebrane przez nas dane osobowe odpowiedniemu następcy strony trzeciej.

Ochrona danych osobowych

Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – w celu ochrony Twoich danych osobowych przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także przed nieautoryzowanym dostępem, ujawnieniem, zmianą i zniszczeniem.

Zachowanie prywatności na poziomie firmy

Aby zapewnić bezpieczeństwo danych osobowych, informujemy naszych pracowników o praktykach dotyczących prywatności i bezpieczeństwa oraz ściśle egzekwujemy praktyki dotyczące prywatności.