Le equazioni trigonometriche più semplici sono le equazioni
Cos(x)=a, sin(x)=a, tg(x)=a, ctg(x)=a
Equazione cos(x) = a

Spiegazione e motivazione
- Le radici dell'equazione cosx = a. Quando | un | > 1 l'equazione non ha radici perché | cosx |< 1 для любого x (прямая y = а при а >1 o a< -1 не пересекает график функцииy = cosx).
Lasciate | un |< 1. Тогда прямая у = а пересекает график функции
y = cos x. Sull'intervallo, la funzione y = cos x diminuisce da 1 a -1. Ma una funzione decrescente assume ciascuno dei suoi valori solo in un punto del suo dominio di definizione, quindi l'equazione cos x = a ha una sola radice su questo intervallo, che, per definizione dell'arcocoseno, è: x 1 = arccos a (e per questa radice cos x = a).
Il coseno è una funzione pari, quindi sull'intervallo [-n; 0] l'equazione cos x = e ha anche una sola radice - il numero opposto a x 1, cioè
x 2 = -arcos a.
Quindi, sull'intervallo [-n; n] (lunghezza 2n) l'equazione cos x = a per | un |< 1 имеет только корни x = ±arccos а.
La funzione y = cos x è periodica con un periodo di 2n, quindi tutte le altre radici differiscono da quelle trovate per 2np (n € Z). Otteniamo la seguente formula per le radici dell'equazione cos x = e quando
x = ± arccos a + 2n, n £ Z.
- Casi particolari di risoluzione dell'equazione cosx = a.
È utile ricordare la notazione speciale per le radici dell'equazione cos x = a quando
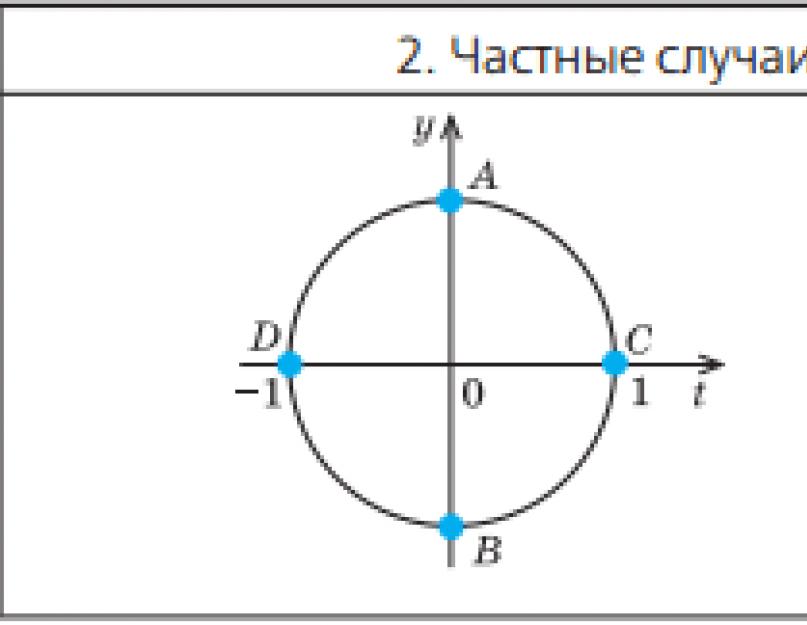
a \u003d 0, a \u003d -1, a \u003d 1, che può essere facilmente ottenuto utilizzando il cerchio unitario come guida.
Poiché il coseno è uguale all'ascissa del punto corrispondente sulla circonferenza unitaria, otteniamo che cos x = 0 se e solo se il punto corrispondente sulla circonferenza unitaria è il punto A o il punto B.
Allo stesso modo, cos x = 1 se e solo se il punto corrispondente della circonferenza unitaria è il punto C, quindi,
x = 2πp, k€ Z.
Anche cos x \u003d -1 se e solo se il punto corrispondente della circonferenza unitaria è il punto D, quindi x \u003d n + 2n,



Equazione sin(x) = a


Spiegazione e motivazione
- Le radici dell'equazione sinx = a. Quando | un | > 1 l'equazione non ha radici perché | sinx |< 1 для любого x (прямая y = а на рисунке при а >1 o a< -1 не пересекает график функции y = sinx).
I metodi principali per risolvere le equazioni trigonometriche sono: ridurre le equazioni a quelle più semplici (usando formule trigonometriche), introdurre nuove variabili e fattorizzare. Consideriamo la loro applicazione con esempi. Prestare attenzione alla progettazione della soluzione delle equazioni trigonometriche.
Una condizione necessaria per la riuscita soluzione delle equazioni trigonometriche è la conoscenza delle formule trigonometriche (argomento 13 del lavoro 6).
Esempi.
1. Equazioni che si riducono al più semplice.
1) Risolvi l'equazione
Soluzione:
Risposta:
2) Trova le radici dell'equazione
(sinx + cosx) 2 = 1 – sinxcosx appartenente al segmento .
Soluzione:
Risposta:
2. Equazioni che si riducono a equazioni quadratiche.
1) Risolvi l'equazione 2 sin 2 x - cosx -1 = 0.
Soluzione: Usando la formula sin 2 x \u003d 1 - cos 2 x, otteniamo
Risposta:
2) Risolvi l'equazione cos 2x = 1 + 4 cosx.
Soluzione: Usando la formula cos 2x = 2 cos 2 x - 1, otteniamo
Risposta:
3) Risolvi l'equazione tgx - 2ctgx + 1 = 0
Soluzione:
Risposta:
3. Equazioni omogenee
1) Risolvi l'equazione 2sinx - 3cosx = 0
Soluzione: Sia cosx = 0, quindi 2sinx = 0 e sinx = 0 - una contraddizione con il fatto che sin 2 x + cos 2 x = 1. Quindi cosx ≠ 0 e puoi dividere l'equazione per cosx. Ottenere
Risposta:
2) Risolvi l'equazione 1 + 7 cos 2 x = 3 sin 2x
Soluzione:
Usando le formule 1 = sin 2 x + cos 2 x e sin 2x = 2 sinxcosx, otteniamo
sin2x + cos2x + 7cos2x = 6sinxcosx
sin2x - 6sinxcosx+ 8cos2x = 0
Sia cosx = 0, quindi sin 2 x = 0 e sinx = 0 - una contraddizione con il fatto che sin 2 x + cos 2 x = 1.
Quindi cosx ≠ 0 e possiamo dividere l'equazione per cos 2 x .
Ottenere
tg 2x – 6 tgx + 8 = 0
Denota tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y2=2
a) tanx = 4, x= arctg4 + 2 K, K
b) tgx = 2, x= arctg2 + 2 K, K .
Risposta: arctg4 + 2 K, arctan2 + 2 k, k
4. Equazioni della forma un sinx + b cosx = con con≠ 0.
1) Risolvi l'equazione.
Soluzione:
Risposta:
5. Equazioni risolte per fattorizzazione.
1) Risolvi l'equazione sin2x - sinx = 0.
La radice dell'equazione f (X) = φ ( X) può servire solo come numero 0. Controlliamo questo:
cos 0 = 0 + 1 - l'uguaglianza è vera.
Il numero 0 è l'unica radice di questa equazione.
Risposta: 0.
Puoi ordinare una soluzione dettagliata al tuo problema !!!
Un'uguaglianza contenente un'incognita sotto il segno di una funzione trigonometrica (`sin x, cos x, tg x` o `ctg x`) è chiamata equazione trigonometrica e considereremo ulteriormente le loro formule.
Le equazioni più semplici sono `sin x=a, cos x=a, tg x=a, ctg x=a`, dove `x` è l'angolo da trovare, `a` è un numero qualsiasi. Scriviamo le formule radice per ciascuno di essi.
1. Equazione `sin x=a`.
Per `|a|>1` non ha soluzioni.
Con `|a| \leq 1` ha un numero infinito di soluzioni.
Formula radice: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Equazione `cos x=a`
Per `|a|>1` - come nel caso del seno, non ci sono soluzioni tra i numeri reali.
Con `|a| \leq 1` ha un numero infinito di soluzioni.
Formula radice: `x=\pm arccos a + 2\pi n, n \in Z`

Casi speciali per seno e coseno nei grafici. 
3. Equazione `tg x=a`
Ha un numero infinito di soluzioni per qualsiasi valore di `a`.
Formula radice: `x=arctg a + \pi n, n \in Z`

4. Equazione `ctg x=a`
Ha anche un numero infinito di soluzioni per qualsiasi valore di `a`.
Formula radice: `x=arcctg a + \pi n, n \in Z`

Formule per le radici delle equazioni trigonometriche nella tabella
Per seno:  Per coseno:
Per coseno:  Per tangente e cotangente:
Per tangente e cotangente:  Formule per la risoluzione di equazioni contenenti funzioni trigonometriche inverse:
Formule per la risoluzione di equazioni contenenti funzioni trigonometriche inverse:

Metodi per la risoluzione di equazioni trigonometriche
La soluzione di qualsiasi equazione trigonometrica consiste in due fasi:
- usando per convertirlo nel più semplice;
- risolvere la semplice equazione risultante usando le formule precedenti per le radici e le tabelle.
Consideriamo i principali metodi di soluzione usando esempi.
metodo algebrico.
In questo metodo viene eseguita la sostituzione di una variabile e la sua sostituzione in uguaglianza.
Esempio. Risolvi l'equazione: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
fare una sostituzione: `cos(x+\frac \pi 6)=y`, quindi `2y^2-3y+1=0`,
troviamo le radici: `y_1=1, y_2=1/2`, da cui seguono due casi:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.
Risposta: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Fattorizzazione.
Esempio. Risolvi l'equazione: `sin x+cos x=1`.
Soluzione. Sposta a sinistra tutti i termini di uguaglianza: `sin x+cos x-1=0`. Usando , trasformiamo e fattorizziamo il lato sinistro:
`peccato x - 2peccato^2 x/2=0`,
`2peccato x/2 cos x/2-2peccato^2 x/2=0`,
`2peccato x/2 (cos x/2-peccato x/2)=0`,
- `peccato x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.
Risposta: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Riduzione ad un'equazione omogenea
Innanzitutto, devi portare questa equazione trigonometrica in una delle due forme seguenti:
`a sin x+b cos x=0` (equazione omogenea di primo grado) o `a sin^2 x + b sin x cos x +c cos^2 x=0` (equazione omogenea di secondo grado).
Quindi dividi entrambe le parti per `cos x \ne 0` per il primo caso e per `cos^2 x \ne 0` per il secondo. Otteniamo le equazioni per `tg x`: `a tg x+b=0` e `a tg^2 x + b tg x +c =0`, che devono essere risolte usando metodi noti.
Esempio. Risolvi l'equazione: `2 sin^2 x+sin x cos x - cos^2 x=1`.
Soluzione. Scriviamo il lato destro come `1=sin^2 x+cos^2 x`:
`2 sin^2 x+peccato x cos x — cos^2 x=` `peccato^2 x+cos^2 x`,
`2 sin^2 x+peccato x cos x - cos^2 x -` ` sin^2 x - cos^2 x=0`
`peccato^2 x+peccato x cos x - 2 cos^2 x=0`.
Questa è un'equazione trigonometrica omogenea di secondo grado, dividendo i suoi lati sinistro e destro per `cos^2 x \ne 0`, otteniamo:
`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) - \frac(2 cos^2 x)(cos^2 x)=0`
`tg^2 x+tg x - 2=0`. Introduciamo la sostituzione `tg x=t`, come risultato `t^2 + t - 2=0`. Le radici di questa equazione sono `t_1=-2` e `t_2=1`. Quindi:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Risposta. `x_1=arco (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Vai a Mezzo angolo
Esempio. Risolvi l'equazione: `11 sin x - 2 cos x = 10`.
Soluzione. Applicando le formule del doppio angolo, il risultato è: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`
`4 tg^2 x/2 - 11 tg x/2 +6=0`
Applicando il metodo algebrico sopra descritto, otteniamo:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Risposta. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arco 3/4+2\pi n`, `n \in Z`.
Introduzione di un angolo ausiliario
Nell'equazione trigonometrica `a sin x + b cos x =c`, dove a,b,c sono coefficienti e x è una variabile, dividiamo entrambe le parti per `sqrt (a^2+b^2)`:
`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) +b^2))`.
I coefficienti sul lato sinistro hanno le proprietà di seno e coseno, cioè la somma dei loro quadrati è 1 e il loro modulo è al massimo 1. Indichiamoli come segue: `\frac a(sqrt (a^2+b^ 2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2))=C` , poi:
`cos \varphi sin x + sin \varphi cos x =C`.
Diamo un'occhiata più da vicino al seguente esempio:
Esempio. Risolvi l'equazione: `3 sin x+4 cos x=2`.
Soluzione. Dividendo entrambi i membri dell'equazione per `sqrt (3^2+4^2)`, otteniamo:
`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))`
`3/5 sin x+4/5 cos x=2/5`.
Denota `3/5 = cos \varphi` , `4/5=peccato \varphi`. Poiché `sin \varphi>0`, `cos \varphi>0`, prendiamo `\varphi=arcsin 4/5` come angolo ausiliario. Quindi scriviamo la nostra uguaglianza nella forma:
`cos \varphi sin x+sin \varphi cos x=2/5`
Applicando la formula per la somma degli angoli per il seno, scriviamo la nostra uguaglianza nella forma seguente:
`peccato(x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Risposta. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Equazioni trigonometriche frazionario-razionali
Si tratta di uguaglianze con frazioni, nei cui numeratori e denominatori sono presenti funzioni trigonometriche.
Esempio. Risolvi l'equazione. `\frac (peccato x)(1+cos x)=1-cos x`.
Soluzione. Moltiplica e dividi il lato destro dell'equazione per `(1+cos x)`. Di conseguenza, otteniamo:
`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`
`\frac (sin x-sin^2 x)(1+cos x)=0`
Dato che il denominatore non può essere zero, otteniamo `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Uguaglia il numeratore della frazione a zero: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Quindi `sin x=0` o `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-peccato x=0`, `peccato x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Dato che ` x \ne \pi+2\pi n, n \in Z`, le soluzioni sono `x=2\pi n, n \in Z` e `x=\pi /2+2\pi n` , `n \in Z`.
Risposta. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
La trigonometria, e in particolare le equazioni trigonometriche, sono utilizzate in quasi tutte le aree della geometria, della fisica e dell'ingegneria. Lo studio inizia al decimo anno, ci sono sempre compiti per l'esame, quindi cerca di ricordare tutte le formule delle equazioni trigonometriche: ti torneranno sicuramente utili!
Tuttavia, non è nemmeno necessario memorizzarli, l'importante è capirne l'essenza ed essere in grado di dedurli. Non è così difficile come sembra. Guarda tu stesso guardando il video.
Il videocorso "Prendi una A" include tutti gli argomenti necessari per il superamento dell'esame di matematica con 60-65 punti. Completamente tutte le attività 1-13 del profilo USE in matematica. Adatto anche per il superamento del Basic USE in matematica. Se vuoi superare l'esame con 90-100 punti, devi risolvere la parte 1 in 30 minuti e senza errori!
Corso di preparazione all'esame per le classi 10-11, oltre che per docenti. Tutto il necessario per risolvere la parte 1 dell'esame di matematica (i primi 12 problemi) e il problema 13 (trigonometria). E questo è più di 70 punti all'Esame di Stato Unificato, e né uno studente da cento punti né un umanista possono farne a meno.
Tutta la teoria necessaria. Soluzioni rapide, trappole e segreti dell'esame. Sono stati analizzati tutti i compiti rilevanti della parte 1 dei compiti della Banca della FIPI. Il corso è pienamente conforme ai requisiti dell'USE-2018.
Il corso contiene 5 grandi argomenti, 2,5 ore ciascuno. Ogni argomento è dato da zero, in modo semplice e chiaro.
Centinaia di compiti d'esame. Problemi di testo e teoria della probabilità. Algoritmi di problem solving semplici e facili da ricordare. Geometria. Teoria, materiale di riferimento, analisi di tutti i tipi di compiti USE. Stereometria. Trucchi astuti per la risoluzione, utili cheat sheet, sviluppo dell'immaginazione spaziale. Trigonometria da zero - al compito 13. Capire invece di stipare. Spiegazione visiva di concetti complessi. Algebra. Radici, potenze e logaritmi, funzione e derivata. Base per la risoluzione di problemi complessi della 2a parte dell'esame.
La tua privacy è importante per noi. Per questo motivo, abbiamo sviluppato un'Informativa sulla privacy che descrive come utilizziamo e memorizziamo le tue informazioni. Si prega di leggere la nostra politica sulla privacy e di farci sapere se avete domande.
Raccolta e utilizzo delle informazioni personali
Le informazioni personali si riferiscono a dati che possono essere utilizzati per identificare o contattare una persona specifica.
È possibile che ti venga chiesto di fornire le tue informazioni personali in qualsiasi momento quando ci contatti.
Di seguito sono riportati alcuni esempi dei tipi di informazioni personali che potremmo raccogliere e di come potremmo utilizzare tali informazioni.
Quali informazioni personali raccogliamo:
- Quando invii una domanda sul sito, potremmo raccogliere varie informazioni, incluso il tuo nome, numero di telefono, indirizzo e-mail, ecc.
Come utilizziamo le tue informazioni personali:
- Le informazioni personali che raccogliamo ci consentono di contattarti e informarti su offerte uniche, promozioni e altri eventi e eventi imminenti.
- Di tanto in tanto, potremmo utilizzare le tue informazioni personali per inviarti avvisi e comunicazioni importanti.
- Possiamo anche utilizzare le informazioni personali per scopi interni, come condurre audit, analisi dei dati e ricerche varie al fine di migliorare i servizi che forniamo e fornire consigli sui nostri servizi.
- Se partecipi a un'estrazione a premi, un concorso o un incentivo simile, potremmo utilizzare le informazioni fornite per amministrare tali programmi.
Divulgazione a terzi
Non divulghiamo le informazioni ricevute da te a terzi.
Eccezioni:
- Nel caso in cui sia necessario - in conformità con la legge, l'ordine giudiziario, in procedimenti legali e/o sulla base di richieste pubbliche o richieste di enti statali nel territorio della Federazione Russa - divulgare le tue informazioni personali. Potremmo anche divulgare informazioni su di te se stabiliamo che tale divulgazione è necessaria o appropriata per motivi di sicurezza, applicazione della legge o altri motivi di interesse pubblico.
- In caso di riorganizzazione, fusione o vendita, potremmo trasferire le informazioni personali che raccogliamo al successore di terze parti pertinente.
Protezione delle informazioni personali
Adottiamo precauzioni, comprese quelle amministrative, tecniche e fisiche, per proteggere le tue informazioni personali da perdita, furto e uso improprio, nonché da accesso, divulgazione, alterazione e distruzione non autorizzati.
Mantenere la privacy a livello aziendale
Per garantire che le tue informazioni personali siano al sicuro, comunichiamo le pratiche di privacy e sicurezza ai nostri dipendenti e applichiamo rigorosamente le pratiche sulla privacy.