Vienkāršākie trigonometriskie vienādojumi ir vienādojumi

Cos(x)=a, sin(x)=a, tg(x)=a, ctg(x)=a

Vienādojums cos(x) = a

Paskaidrojums un pamatojums

1. Vienādojuma saknes cosx = a. Kad | a | > 1 vienādojumam nav sakņu, jo | cosx |< 1 для любого x (прямая y = а при а >1 vai pie a< -1 не пересекает график функцииy = cosx).

Ļaujiet | a |< 1. Тогда прямая у = а пересекает график функции

y = cos x. Intervālā funkcija y = cos x samazinās no 1 līdz -1. Bet dilstoša funkcija katru no savām vērtībām iegūst tikai vienā definīcijas apgabala punktā, tāpēc vienādojumam cos x = a šajā intervālā ir tikai viena sakne, kas pēc loka kosinusa definīcijas ir: x 1 = arccos a (un šai saknei cos x = a).

Kosinuss ir pāra funkcija, tāpēc uz intervāla [-n; 0] vienādojums cos x = un tam ir tikai viena sakne - skaitlis, kas ir pretējs x 1, tas ir

x 2 = -arccos a.

Tādējādi uz intervāla [-n; n] (garums 2n) vienādojums cos x = a | a |< 1 имеет только корни x = ±arccos а.

Funkcija y = cos x ir periodiska ar periodu 2n, tāpēc visas pārējās saknes atšķiras no tām, kuras atrod ar 2np (n € Z). Mēs iegūstam šādu formulu vienādojuma cos x = un kad saknēm

x = ± arccos a + 2n, n £ Z.

1. Īpaši vienādojuma cosx = a risināšanas gadījumi.

Ir lietderīgi atcerēties īpašo apzīmējumu vienādojuma cos x = a kad saknēm

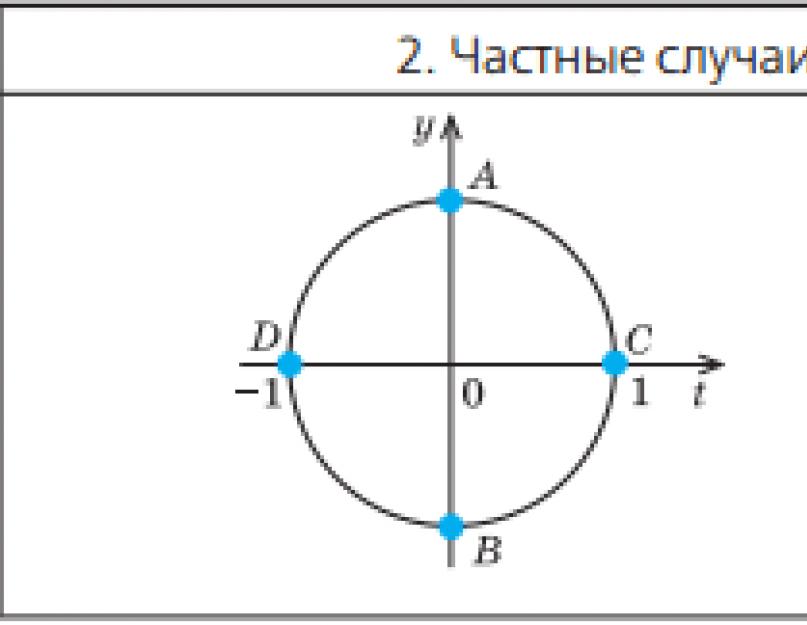
a \u003d 0, a \u003d -1, a \u003d 1, ko var viegli iegūt, kā ceļvedi izmantojot vienības apli.

Tā kā kosinuss ir vienāds ar vienības apļa atbilstošā punkta abscisu, mēs iegūstam, ka cos x = 0 tad un tikai tad, ja atbilstošais punkts uz vienības apļa ir punkts A vai punkts B.

Līdzīgi cos x = 1 tad un tikai tad, ja atbilstošais vienības apļa punkts ir punkts C, tāpēc

x = 2πp, k € Z.

Arī cos x \u003d -1 tad un tikai tad, ja vienības apļa atbilstošais punkts ir punkts D, tādējādi x \u003d n + 2n,

Vienādojums sin(x) = a

Paskaidrojums un pamatojums

1. Saknes vienādojumam sinx = a. Kad | a | > 1 vienādojumam nav sakņu, jo | sinx |< 1 для любого x (прямая y = а на рисунке при а >1 vai pie a< -1 не пересекает график функции y = sinx).

Galvenās metodes trigonometrisko vienādojumu risināšanai ir: vienādojumu samazināšana līdz vienkāršākajiem (izmantojot trigonometriskās formulas), jaunu mainīgo ieviešana un faktorings. Apskatīsim to pielietojumu ar piemēriem. Pievērsiet uzmanību trigonometrisko vienādojumu risinājuma dizainam.

Nepieciešams nosacījums veiksmīgam trigonometrisko vienādojumu risinājumam ir trigonometrisko formulu zināšanas (6. darba 13. tēma).

Piemēri.

1. Reducēšana uz vienkāršākajiem vienādojumiem.

1) Atrisiniet vienādojumu

Risinājums:

Atbilde:

2) Atrodiet vienādojuma saknes

(sinx + cosx) 2 = 1 – segmentam piederošais sinxcosx .

Risinājums:

Atbilde:

2. Vienādojumi, kas reducēti uz kvadrātvienādojumiem.

1) Atrisiniet vienādojumu 2 sin 2 x - cosx -1 = 0.

Risinājums: Izmantojot formulu sin 2 x \u003d 1 - cos 2 x, mēs iegūstam

Atbilde:

2) Atrisiniet vienādojumu cos 2x = 1 + 4 cosx.

Risinājums: Izmantojot formulu cos 2x = 2 cos 2 x - 1, mēs iegūstam

Atbilde:

3) Atrisiniet vienādojumu tgx - 2ctgx + 1 = 0

Risinājums:

Atbilde:

3. Homogēni vienādojumi

1) Atrisiniet vienādojumu 2sinx - 3cosx = 0

Risinājums: Lai cosx = 0, tad 2sinx = 0 un sinx = 0 - pretruna ar to, ka sin 2 x + cos 2 x = 1. Tātad cosx ≠ 0 un vienādojumu var dalīt ar cosx. gūt

Atbilde:

2) Atrisiniet vienādojumu 1 + 7 cos 2 x = 3 sin 2x

Risinājums:

Izmantojot formulas 1 = sin 2 x + cos 2 x un sin 2x = 2 sinxcosx, mēs iegūstam

sin2x + cos2x + 7cos2x = 6sinxcosx
sin2x — 6sinxcosx+ 8cos2x = 0

Lai cosx = 0, tad sin 2 x = 0 un sinx = 0 - pretruna ar to, ka sin 2 x + cos 2 x = 1.
Tātad cosx ≠ 0 un mēs varam dalīt vienādojumu ar cos 2 x . gūt

tg 2x – 6 tgx + 8 = 0
Apzīmējiet tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y2=2
a) tanx = 4, x = arctg4 + 2 k, k
b) tgx = 2, x = arctg2 + 2 k, k .

Atbilde: arctg4+2 k, arctan2 + 2 labi labi

4. Formas vienādojumi a sinx + b cosx = ar, ar≠ 0.

1) Atrisiniet vienādojumu.

Risinājums:

Atbilde:

5. Faktorizācijas vienādojumi.

1) Atrisiniet vienādojumu sin2x - sinx = 0.

Vienādojuma sakne f (X) = φ ( X) var kalpot tikai kā skaitlis 0. Pārbaudīsim šo:

cos 0 = 0 + 1 - vienādība ir patiesa.

Skaitlis 0 ir vienīgā šī vienādojuma sakne.

Atbilde: 0.

Jūs varat pasūtīt detalizētu savas problēmas risinājumu!!!

Vienādību, kas satur nezināmo zem trigonometriskās funkcijas zīme (`sin x, cos x, tg x` vai `ctg x`), sauc par trigonometrisko vienādojumu, un mēs tālāk aplūkosim to formulas.

Vienkāršākie vienādojumi ir “sin x=a, cos x=a, tg x=a, ctg x=a”, kur “x” ir atrodamais leņķis, bet “a” ir jebkurš skaitlis. Uzrakstīsim katrai no tām saknes formulas.

1. Vienādojums "sin x=a".

`|a|>1` tam nav risinājumu.

Ar `|a| \leq 1` ir bezgalīgs atrisinājumu skaits.

Saknes formula: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Vienādojums cos x=a

`|a|>1` — tāpat kā sinusa gadījumā, starp reāliem skaitļiem nav atrisinājumu.

Ar `|a| \leq 1` ir bezgalīgs atrisinājumu skaits.

Saknes formula: `x=\pm arccos a + 2\pi n, n \in Z`

Īpaši gadījumi sinusam un kosinusam grafikos.

3. Vienādojums “tg x=a”.

Ir bezgalīgs skaits risinājumu jebkurai “a” vērtībai.

Saknes formula: `x=arctg a + \pi n, n \in Z`

4. Vienādojums “ctg x=a”.

Tam ir arī bezgalīgs skaits risinājumu jebkurai “a” vērtībai.

Saknes formula: `x=arcctg a + \pi n, n \in Z`

Formulas trigonometrisko vienādojumu saknēm tabulā

Sinusam:
Kosinusam:
Pieskarei un kotangensei:
Formulas vienādojumu risināšanai, kas satur apgrieztas trigonometriskās funkcijas:

Trigonometrisko vienādojumu risināšanas metodes

Jebkura trigonometriskā vienādojuma atrisināšana sastāv no diviem posmiem:

• izmantojot, lai to pārvērstu par vienkāršāko;
• atrisiniet iegūto vienkāršo vienādojumu, izmantojot iepriekš minētās sakņu un tabulu formulas.

Apsvērsim galvenās risinājuma metodes, izmantojot piemērus.

algebriskā metode.

Šajā metodē tiek veikta mainīgā aizstāšana un tā aizstāšana ar vienādību.

Piemērs. Atrisiniet vienādojumu: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0,

veiciet nomaiņu: "cos(x+\frac \pi 6)=y", pēc tam "2y^2-3y+1=0",

mēs atrodam saknes: `y_1=1, y_2=1/2`, no kurām izriet divi gadījumi:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Atbilde: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Faktorizācija.

Piemērs. Atrisiniet vienādojumu: `sin x+cos x=1`.

Risinājums. Pārvietojiet pa kreisi visus vienlīdzības nosacījumus: "sin x+cos x-1=0". Izmantojot , mēs pārveidojam un faktorizējam kreiso pusi:

"sin x - 2sin^2 x/2=0",

"2sin x/2 cos x/2-2sin^2 x/2=0",

"2sin x/2 (cos x/2-sin x/2)=0",

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. "cos x/2-sin x/2=0", "tg x/2=1", "x/2=arctg 1+ \pi n", "x/2=\pi/4+ \pi n" , `x_2=\pi/2+ 2\pi n`.

Atbilde: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Reducēšana uz homogēnu vienādojumu

Pirmkārt, šis trigonometriskais vienādojums ir jāsadala vienā no divām formām:

`a sin x+b cos x=0` (pirmās pakāpes homogēns vienādojums) vai `a sin^2 x + b sin x cos x +c cos^2 x=0` (otrās pakāpes homogēns vienādojums).

Pēc tam sadaliet abas daļas ar “cos x \ne 0” pirmajā gadījumā un ar “cos^2 x \ ne 0” otrajā gadījumā. Mēs iegūstam `tg x` vienādojumus: `a tg x+b=0` un `a tg^2 x + b tg x +c =0`, kas jāatrisina, izmantojot zināmas metodes.

Piemērs. Atrisiniet vienādojumu: `2 sin^2 x+sin x cos x - cos^2 x=1`.

Risinājums. Labajā pusē rakstīsim kā `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x',

`2 sin^2 x+sin x cos x - cos^2 x -` ` sin^2 x - cos^2 x=0`

`sin^2 x+sin x cos x — 2 cos^2 x=0`.

Šis ir homogēns otrās pakāpes trigonometriskais vienādojums, kura kreiso un labo pusi dalot ar `cos^2 x \ne 0`, iegūstam:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) - \frac(2 cos^2 x)(cos^2 x)=0

`tg^2 x+tg x - 2=0'. Ieviesīsim aizstāšanu `tg x=t`, kā rezultātā `t^2 + t - 2=0`. Šī vienādojuma saknes ir `t_1=-2` un `t_2=1`. Pēc tam:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z.

Atbilde. `x_1=arctg (-2)+\pi n`, `n \in Z, `x_2=\pi/4+\pi n`, `n \in Z`.

Dodieties uz Half Corner

Piemērs. Atrisiniet vienādojumu: `11 sin x - 2 cos x = 10`.

Risinājums. Lietojot dubultā leņķa formulas, rezultāts ir: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`

`4 tg^2 x/2 — 11 tg x/2 +6=0

Izmantojot iepriekš aprakstīto algebrisko metodi, mēs iegūstam:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z',
2. `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Atbilde. `x_1=2 arctg 2+2\pi n, n \in Z, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Palīgleņķa ieviešana

Trigonometriskajā vienādojumā `a sin x + b cos x =c`, kur a,b,c ir koeficienti un x ir mainīgais, mēs abas daļas sadalām ar `sqrt (a^2+b^2)`:

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) +b^2))".

Koeficientiem kreisajā pusē ir sinusa un kosinusa īpašības, proti, to kvadrātu summa ir 1 un modulis ir ne vairāk kā 1. Apzīmēsim tos šādi: `\frac a(sqrt (a^2+b^ 2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2))=C` , tad:

`cos \varphi sin x + sin \varphi cos x =C`.

Apskatīsim tuvāk šādu piemēru:

Piemērs. Atrisiniet vienādojumu: `3 sin x+4 cos x=2`.

Risinājums. Sadalot abas vienādojuma puses ar `sqrt (3^2+4^2)`, iegūstam:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))".

"3/5 sin x+4/5 cos x=2/5".

Apzīmē `3/5 = cos \varphi` , `4/5=sin \varphi`. Tā kā `sin \varphi>0`, `cos \varphi>0`, mēs ņemam `\varphi=arcsin 4/5` kā palīgleņķi. Tad mēs rakstām savu vienādību formā:

`cos \varphi sin x+sin \varphi cos x=2/5`

Piemērojot sinusa leņķu summas formulu, mēs rakstām savu vienādību šādā formā:

`sin(x+\varphi)=2/5,

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Atbilde. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Frakcionāli-racionālie trigonometriskie vienādojumi

Tās ir vienādības ar daļskaitļiem, kuru skaitītājos un saucējos ir trigonometriskās funkcijas.

Piemērs. Atrisiniet vienādojumu. `\frac (sin x)(1+cos x)=1-cos x.

Risinājums. Reiziniet un sadaliet vienādojuma labo pusi ar (1+cos x)”. Rezultātā mēs iegūstam:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0

`\frac (sin x-sin^2 x)(1+cos x)=0

Ņemot vērā, ka saucējs nevar būt nulle, mēs iegūstam `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z.

Pielīdziniet daļskaitļa skaitītāju nullei: "sin x-sin^2 x=0", "sin x(1-sin x)=0". Pēc tam “sin x=0” vai “1-sin x=0”.

1. `sin x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

Ņemot vērā, ka ` x \ne \pi+2\pi n, n \in Z, risinājumi ir `x=2\pi n, n \in Z` un `x=\pi /2+2\pi n` , `n \in Z`.

Atbilde. "x=2\pi n", "n \in Z", "x=\pi /2+2\pi n", "n \in Z".

Trigonometrija un jo īpaši trigonometriskie vienādojumi tiek izmantoti gandrīz visās ģeometrijas, fizikas un inženierzinātņu jomās. Mācības sākas 10. klasē, eksāmenam vienmēr ir uzdevumi, tāpēc centies atcerēties visas trigonometrisko vienādojumu formulas – tās tev noteikti noderēs!

Tomēr jums tie pat nav jāiegaumē, galvenais ir saprast būtību un spēt secināt. Tas nav tik grūti, kā šķiet. Pārliecinies pats, noskatoties video.

Videokursā "Saņem A" iekļautas visas tēmas, kas nepieciešamas matemātikas eksāmena sekmīgai nokārtošanai par 60-65 punktiem. Pilnīgi visi profila USE uzdevumi 1-13 matemātikā. Piemērots arī matemātikas pamatizmantošanas kursa nokārtošanai. Ja vēlies eksāmenu nokārtot ar 90-100 punktiem, 1.daļa jāatrisina 30 minūtēs un bez kļūdām!

Sagatavošanas kurss eksāmenam 10.-11.klasei, kā arī skolotājiem. Viss nepieciešamais, lai atrisinātu eksāmena 1. daļu matemātikā (pirmās 12 problēmas) un 13. uzdevumu (trigonometrija). Un tas ir vairāk nekā 70 punkti vienotajā valsts eksāmenā, un bez tiem nevar iztikt ne simt ballu students, ne humānists.

Visa nepieciešamā teorija. Eksāmena ātrie risinājumi, lamatas un noslēpumi. Analizēti visi būtiskie FIPI bankas 1. daļas uzdevumi. Kurss pilnībā atbilst USE-2018 prasībām.

Kursā ir 5 lielas tēmas, katra 2,5 stundas. Katra tēma ir dota no nulles, vienkārši un skaidri.

Simtiem eksāmenu uzdevumu. Teksta problēmas un varbūtību teorija. Vienkārši un viegli iegaumējami problēmu risināšanas algoritmi. Ģeometrija. Teorija, izziņas materiāls, visu veidu USE uzdevumu analīze. Stereometrija. Viltīgi triki risināšanai, noderīgas blēžu lapas, telpiskās iztēles attīstīšana. Trigonometrija no nulles - līdz 13. uzdevumam. Sapratne, nevis pieblīvēšanās. Sarežģītu jēdzienu vizuāls skaidrojums. Algebra. Saknes, pakāpes un logaritmi, funkcija un atvasinājums. Eksāmena 2. daļas sarežģītu uzdevumu risināšanas bāze.

Jūsu privātums mums ir svarīgs. Šī iemesla dēļ mēs esam izstrādājuši Privātuma politiku, kurā aprakstīts, kā mēs izmantojam un uzglabājam jūsu informāciju. Lūdzu, izlasiet mūsu privātuma politiku un informējiet mūs, ja jums ir kādi jautājumi.

Personiskās informācijas vākšana un izmantošana

Personiskā informācija attiecas uz datiem, kurus var izmantot, lai identificētu vai sazinātos ar konkrētu personu.

Jums var tikt lūgts sniegt savu personisko informāciju jebkurā laikā, kad sazināsieties ar mums.

Tālāk ir sniegti daži piemēri par to, kāda veida personas informāciju mēs varam vākt un kā mēs varam izmantot šādu informāciju.

Kādu personas informāciju mēs apkopojam:

• Kad jūs iesniedzat pieteikumu vietnē, mēs varam apkopot dažādu informāciju, tostarp jūsu vārdu, tālruņa numuru, e-pasta adresi utt.

Kā mēs izmantojam jūsu personisko informāciju:

• Mūsu apkopotā personas informācija ļauj mums sazināties ar jums un informēt par unikāliem piedāvājumiem, akcijām un citiem notikumiem un gaidāmajiem pasākumiem.
• Laiku pa laikam mēs varam izmantot jūsu personisko informāciju, lai nosūtītu jums svarīgus paziņojumus un paziņojumus.
• Mēs varam izmantot personas informāciju arī iekšējiem mērķiem, piemēram, auditu, datu analīzes un dažādu pētījumu veikšanai, lai uzlabotu mūsu sniegtos pakalpojumus un sniegtu jums ieteikumus par mūsu pakalpojumiem.
• Ja piedalāties balvu izlozē, konkursā vai līdzīgā stimulā, mēs varam izmantot jūsu sniegto informāciju, lai pārvaldītu šādas programmas.

Izpaušana trešajām personām

Mēs neizpaužam no jums saņemto informāciju trešajām personām.

Izņēmumi:

• Gadījumā, ja tas ir nepieciešams - saskaņā ar likumu, tiesas rīkojumu, tiesvedībā un/vai pamatojoties uz publiskiem pieprasījumiem vai valsts iestāžu pieprasījumiem Krievijas Federācijas teritorijā - izpaust savu personas informāciju. Mēs varam arī izpaust informāciju par jums, ja konstatēsim, ka šāda izpaušana ir nepieciešama vai piemērota drošības, tiesībaizsardzības vai citu sabiedrības interešu apsvērumu dēļ.
• Reorganizācijas, apvienošanas vai pārdošanas gadījumā mēs varam nodot mūsu apkopoto personas informāciju attiecīgajai trešajai personai, kas pārņēmusi.

Personiskās informācijas aizsardzība

Mēs veicam piesardzības pasākumus, tostarp administratīvus, tehniskus un fiziskus, lai aizsargātu jūsu personisko informāciju pret pazaudēšanu, zādzību un ļaunprātīgu izmantošanu, kā arī no nesankcionētas piekļuves, izpaušanas, pārveidošanas un iznīcināšanas.

Jūsu privātuma saglabāšana uzņēmuma līmenī

Lai nodrošinātu jūsu personiskās informācijas drošību, mēs saviem darbiniekiem paziņojam par privātuma un drošības praksi un stingri īstenojam privātuma praksi.