Die einfachsten trigonometrischen Gleichungen sind die Gleichungen
Cos(x)=a, sin(x)=a, tg(x)=a, ctg(x)=a
Gleichung cos(x) = a

Erklärung und Begründung
- Die Wurzeln der Gleichung cosx = a. Wann | ein | > 1 hat die Gleichung keine Wurzeln, weil | cosx |< 1 для любого x (прямая y = а при а >1 oder bei a< -1 не пересекает график функцииy = cosx).
Lassen Sie | ein |< 1. Тогда прямая у = а пересекает график функции
y = cos x. Auf dem Intervall nimmt die Funktion y = cos x von 1 auf -1 ab. Aber eine abnehmende Funktion nimmt jeden ihrer Werte nur an einem Punkt ihres Definitionsbereichs an, daher hat die Gleichung cos x = a nur eine Wurzel auf diesem Intervall, die nach Definition des Arkuskosinus ist: x 1 = arccos a (und für diese Wurzel cos x = a).
Cosinus ist eine gerade Funktion, also auf dem Intervall [-n; 0] die Gleichung cos x = und hat auch nur eine Wurzel, nämlich die Zahl, die x 1 entgegengesetzt ist
x 2 = -arccos a.
Somit wird im Intervall [-n; n] (Länge 2n) die Gleichung cos x = a für | ein |< 1 имеет только корни x = ±arccos а.
Die Funktion y = cos x ist periodisch mit einer Periode von 2n, daher unterscheiden sich alle anderen Wurzeln von denen, die durch 2np (n € Z) gefunden werden. Wir erhalten die folgende Formel für die Wurzeln der Gleichung cos x = und when
x = ± arccos a + 2n, n £ Z.
- Sonderfälle der Lösung der Gleichung cosx = a.
Es ist nützlich, sich an die spezielle Notation für die Wurzeln der Gleichung cos x = a when zu erinnern
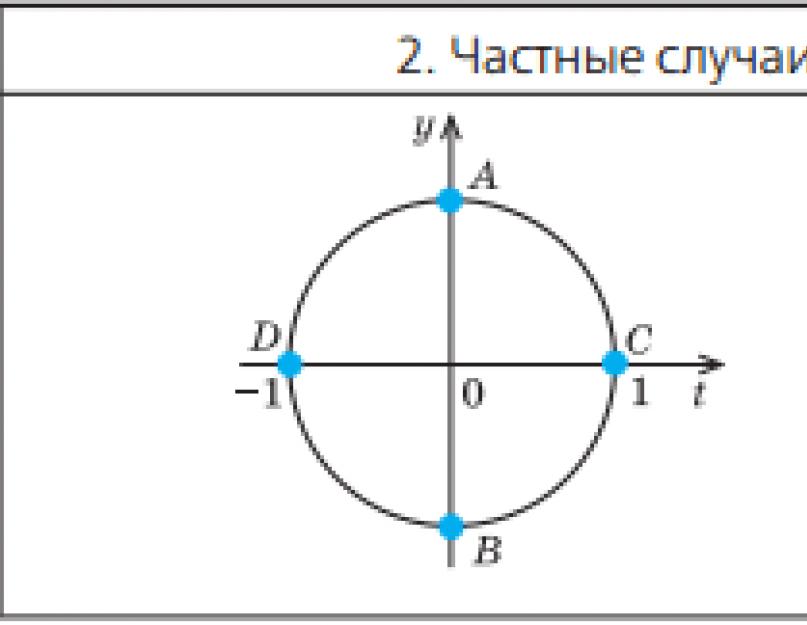
a \u003d 0, a \u003d -1, a \u003d 1, die sich leicht anhand des Einheitskreises als Richtlinie ermitteln lässt.
Da der Kosinus gleich der Abszisse des entsprechenden Punkts auf dem Einheitskreis ist, erhalten wir genau dann cos x = 0, wenn der entsprechende Punkt auf dem Einheitskreis Punkt A oder Punkt B ist.
In ähnlicher Weise ist cos x = 1 genau dann, wenn der entsprechende Punkt des Einheitskreises der Punkt C ist, daher
x = 2πp, k € Z.
Auch cos x \u003d -1 genau dann, wenn der entsprechende Punkt des Einheitskreises der Punkt D ist, also x \u003d n + 2n,



Gleichung sin(x) = a


Erklärung und Begründung
- Die Wurzeln der Gleichung sinx = a. Wann | ein | > 1 hat die Gleichung keine Wurzeln, weil | Sünde |< 1 для любого x (прямая y = а на рисунке при а >1 oder bei a< -1 не пересекает график функции y = sinx).
Die Hauptmethoden zum Lösen trigonometrischer Gleichungen sind: Reduzieren von Gleichungen auf die einfachsten (unter Verwendung trigonometrischer Formeln), Einführen neuer Variablen und Faktorisieren. Betrachten wir ihre Anwendung anhand von Beispielen. Achten Sie auf das Design der Lösung trigonometrischer Gleichungen.
Eine notwendige Voraussetzung für das erfolgreiche Lösen trigonometrischer Gleichungen ist die Kenntnis trigonometrischer Formeln (Thema 13 von Arbeit 6).
Beispiele.
1. Aufs Einfachste reduzierende Gleichungen.
1) Lösen Sie die Gleichung
Lösung:
Antworten:
2) Finden Sie die Wurzeln der Gleichung
(sinx + cosx) 2 = 1 – sinxcosx gehört zum Segment .
Lösung:
Antworten:
2. Gleichungen, die sich auf quadratische Gleichungen reduzieren.
1) Lösen Sie die Gleichung 2 sin 2 x - cosx -1 = 0.
Lösung: Mit der Formel sin 2 x \u003d 1 - cos 2 x erhalten wir
Antworten:
2) Lösen Sie die Gleichung cos 2x = 1 + 4 cosx.
Lösung: Mit der Formel cos 2x = 2 cos 2 x - 1 erhalten wir
Antworten:
3) Lösen Sie die Gleichung tgx - 2ctgx + 1 = 0
Lösung:
Antworten:
3. Homogene Gleichungen
1) Lösen Sie die Gleichung 2sinx - 3cosx = 0
Lösung: Sei cosx = 0, dann 2sinx = 0 und sinx = 0 - ein Widerspruch dazu, dass sin 2 x + cos 2 x = 1 ist. Also ist cosx ≠ 0 und du kannst die Gleichung durch cosx teilen. Erhalten
Antworten:
2) Lösen Sie die Gleichung 1 + 7 cos 2 x = 3 sin 2x
Lösung:
Mit den Formeln 1 = sin 2 x + cos 2 x und sin 2x = 2 sinxcosx erhalten wir
sin2x + cos2x + 7cos2x = 6sinxcosx
sin2x - 6sinxcosx+ 8cos2x = 0
Sei cosx = 0, dann sin 2 x = 0 und sinx = 0 - ein Widerspruch zu der Tatsache, dass sin 2 x + cos 2 x = 1 ist.
Also cosx ≠ 0 und wir können die Gleichung durch cos 2 x teilen .
Erhalten
tg 2x – 6 tgx + 8 = 0
Bezeichne tgx = y
j 2 – 6 j + 8 = 0
y1 = 4; y2=2
a) tanx = 4, x= arctg4 + 2 k, k
b) tgx = 2, x= arctg2 + 2 k, k .
Antworten: arctg4 + 2 k, arctan2 + 2 k, k
4. Gleichungen der Form a sinx + b cos = mit mit≠ 0.
1) Lösen Sie die Gleichung.
Lösung:
Antworten:
5. Durch Faktorisierung gelöste Gleichungen.
1) Lösen Sie die Gleichung sin2x - sinx = 0.
Die Wurzel der Gleichung f (X) = φ ( X) kann nur als Zahl 0 dienen. Lassen Sie uns dies überprüfen:
cos 0 = 0 + 1 - die Gleichheit ist wahr.
Die Zahl 0 ist die einzige Wurzel dieser Gleichung.
Antworten: 0.
Sie können eine detaillierte Lösung Ihres Problems bestellen !!!
Eine Gleichung, die eine Unbekannte unter dem Vorzeichen einer trigonometrischen Funktion (`sin x, cos x, tg x` oder `ctg x`) enthält, wird als trigonometrische Gleichung bezeichnet, und wir werden ihre Formeln weiter betrachten.
Die einfachsten Gleichungen sind `sin x=a, cos x=a, tg x=a, ctg x=a`, wobei `x` der zu findende Winkel ist, `a` eine beliebige Zahl. Lassen Sie uns die Wurzelformeln für jeden von ihnen schreiben.
1. Gleichung „sin x=a“.
Für `|a|>1` hat es keine Lösungen.
Mit `|a| \leq 1` hat unendlich viele Lösungen.
Wurzelformel: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Gleichung `cos x=a`
Für `|a|>1` gibt es - wie beim Sinus - keine Lösungen unter reellen Zahlen.
Mit `|a| \leq 1` hat unendlich viele Lösungen.
Wurzelformel: `x=\pm arccos a + 2\pi n, n \in Z`

Sonderfälle für Sinus und Cosinus in Graphen. 
3. Gleichung „tg x=a“.
Hat unendlich viele Lösungen für beliebige Werte von `a`.
Wurzelformel: `x=arctg a + \pi n, n \in Z`

4. Gleichung „ctg x=a“.
Es hat auch unendlich viele Lösungen für beliebige Werte von `a`.
Wurzelformel: `x=arcctg a + \pi n, n \in Z`

Formeln für die Wurzeln trigonometrischer Gleichungen in der Tabelle
Für Nebenhöhlen:  Für Kosinus:
Für Kosinus:  Für Tangens und Kotangens:
Für Tangens und Kotangens:  Formeln zum Lösen von Gleichungen mit inversen trigonometrischen Funktionen:
Formeln zum Lösen von Gleichungen mit inversen trigonometrischen Funktionen:

Methoden zum Lösen trigonometrischer Gleichungen
Die Lösung einer trigonometrischen Gleichung besteht aus zwei Schritten:
- Verwenden, um es in das einfachste umzuwandeln;
- Lösen Sie die resultierende einfache Gleichung unter Verwendung der obigen Formeln für die Wurzeln und Tabellen.
Betrachten wir die wichtigsten Lösungsmethoden anhand von Beispielen.
algebraische Methode.
Bei dieser Methode erfolgt die Ersetzung einer Variablen und ihre Substitution in Gleichheit.
Beispiel. Lösen Sie die Gleichung: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
Ersetzen: `cos(x+\frac \pi 6)=y`, dann `2y^2-3y+1=0`,
wir finden die Wurzeln: `y_1=1, y_2=1/2`, woraus zwei Fälle folgen:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.
Antwort: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Faktorisierung.
Beispiel. Lösen Sie die Gleichung: `sin x+cos x=1`.
Lösung. Alle Gleichheitsterme nach links verschieben: `sin x+cos x-1=0`. Mit transformieren und faktorisieren wir die linke Seite:
`sünde x - 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.
Antwort: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Reduktion auf eine homogene Gleichung
Zuerst müssen Sie diese trigonometrische Gleichung in eine von zwei Formen bringen:
`a sin x+b cos x=0` (homogene Gleichung ersten Grades) oder `a sin^2 x + b sin x cos x +c cos^2 x=0` (homogene Gleichung zweiten Grades).
Teilen Sie dann beide Teile durch `cos x \ne 0` für den ersten Fall und durch `cos^2 x \ne 0` für den zweiten. Wir erhalten Gleichungen für `tg x`: `a tg x+b=0` und `a tg^2 x + b tg x +c =0`, die mit bekannten Methoden gelöst werden müssen.
Beispiel. Lösen Sie die Gleichung: `2 sin^2 x+sin x cos x - cos^2 x=1`.
Lösung. Schreiben wir die rechte Seite als `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x - cos^2 x -` ` sin^2 x - cos^2 x=0`
`sin^2 x+sin x cos x - 2 cos^2 x=0`.
Dies ist eine homogene trigonometrische Gleichung zweiten Grades, deren linke und rechte Seite durch `cos^2 x \ne 0` dividiert wird, erhalten wir:
`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) - \frac(2 cos^2 x)(cos^2 x)=0`
`tg^2 x+tg x - 2=0`. Führen wir die Ersetzung `tg x=t` ein, als Ergebnis `t^2 + t - 2=0`. Die Wurzeln dieser Gleichung sind `t_1=-2` und `t_2=1`. Dann:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, `n \in Z`.
Antworten. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Gehe zur halben Ecke
Beispiel. Lösen Sie die Gleichung: `11 sin x - 2 cos x = 10`.
Lösung. Bei Anwendung der Doppelwinkelformeln lautet das Ergebnis: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`
`4 tg^2 x/2 - 11 tg x/2 +6=0`
Mit der oben beschriebenen algebraischen Methode erhalten wir:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Antworten. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Einführung eines Hilfswinkels
In der trigonometrischen Gleichung `a sin x + b cos x =c`, wo a,b,c Koeffizienten und x eine Variable sind, dividieren wir beide Teile durch `sqrt (a^2+b^2)`:
`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2 +b^2))`.
Die Koeffizienten auf der linken Seite haben die Eigenschaften von Sinus und Cosinus, nämlich die Summe ihrer Quadrate ist 1 und ihr Betrag ist höchstens 1. Nennen wir sie wie folgt: `\frac a(sqrt (a^2+b^ 2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2))=C` , dann:
`cos \varphi sin x + sin \varphi cos x =C`.
Schauen wir uns das folgende Beispiel genauer an:
Beispiel. Lösen Sie die Gleichung: `3 sin x+4 cos x=2`.
Lösung. Teilen wir beide Seiten der Gleichung durch `sqrt (3^2+4^2)`, erhalten wir:
`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))‘
`3/5 sin x+4/5 cos x=2/5`.
Bezeichne `3/5 = cos \varphi` , `4/5=sin \varphi`. Da `sin \varphi>0`, `cos \varphi>0` ist, nehmen wir als Hilfswinkel `\varphi=arcsin 4/5`. Dann schreiben wir unsere Gleichheit in der Form:
`cos \varphi sin x+sin \varphi cos x=2/5`
Mit der Winkelsummenformel für den Sinus schreiben wir unsere Gleichheit in folgender Form:
`sin(x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Antworten. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Bruchrationale trigonometrische Gleichungen
Dies sind Gleichheiten mit Brüchen, in deren Zählern und Nennern sich trigonometrische Funktionen befinden.
Beispiel. Löse die Gleichung. `\frac (sin x)(1+cos x)=1-cos x`.
Lösung. Multipliziere und dividiere die rechte Seite der Gleichung mit `(1+cos x)`. Als Ergebnis erhalten wir:
`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`
`\frac (sin x-sin^2 x)(1+cos x)=0`
Da der Nenner nicht Null sein kann, erhalten wir `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Den Zähler des Bruchs mit Null gleichsetzen: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Dann `sin x=0` oder `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Da ` x \ne \pi+2\pi n, n \in Z` ist, sind die Lösungen `x=2\pi n, n \in Z` und `x=\pi /2+2\pi n` , `n \in Z`.
Antworten. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Trigonometrie und insbesondere trigonometrische Gleichungen werden in fast allen Bereichen der Geometrie, Physik und Ingenieurwissenschaften verwendet. Das Studium beginnt in der 10. Klasse, es gibt immer Aufgaben für die Prüfung. Versuchen Sie also, sich alle Formeln trigonometrischer Gleichungen zu merken - sie werden Ihnen auf jeden Fall nützlich sein!
Sie müssen sie jedoch nicht einmal auswendig lernen, die Hauptsache ist, die Essenz zu verstehen und daraus schließen zu können. Es ist nicht so schwierig, wie es scheint. Überzeugen Sie sich selbst, indem Sie sich das Video ansehen.
Der Videokurs "Get an A" beinhaltet alle Themen, die für das erfolgreiche Bestehen der Prüfung in Mathematik mit 60-65 Punkten notwendig sind. Erledigen Sie alle Aufgaben 1-13 des Profils USE in Mathematik. Auch zum Bestehen der Basic USE in Mathematik geeignet. Wer die Prüfung mit 90-100 Punkten bestehen will, muss Teil 1 in 30 Minuten und ohne Fehler lösen!
Prüfungsvorbereitungskurs für die Klassen 10-11, sowie für Lehrkräfte. Alles, was Sie brauchen, um Teil 1 der Prüfung in Mathematik (die ersten 12 Aufgaben) und Aufgabe 13 (Trigonometrie) zu lösen. Und das sind mehr als 70 Punkte im Einheitlichen Staatsexamen, und darauf kann weder ein Hundertpunkte-Student noch ein Humanist verzichten.
Die ganze notwendige Theorie. Schnelle Lösungen, Fallen und Geheimnisse der Prüfung. Alle relevanten Aufgaben von Teil 1 der Bank of FIPI-Aufgaben wurden analysiert. Der Kurs entspricht vollständig den Anforderungen des USE-2018.
Der Kurs beinhaltet 5 große Themen zu je 2,5 Stunden. Jedes Thema ist von Grund auf neu, einfach und übersichtlich.
Hunderte von Prüfungsaufgaben. Textprobleme und Wahrscheinlichkeitstheorie. Einfache und leicht zu merkende Problemlösungsalgorithmen. Geometrie. Theorie, Referenzmaterial, Analyse aller Arten von USE-Aufgaben. Stereometrie. Schlaue Tricks zum Lösen, nützliche Spickzettel, Entwicklung des räumlichen Vorstellungsvermögens. Trigonometrie von Grund auf - zu Aufgabe 13. Verstehen statt pauken. Visuelle Erklärung komplexer Konzepte. Algebra. Wurzeln, Potenzen und Logarithmen, Funktion und Ableitung. Basis zur Lösung komplexer Probleme des 2. Teils der Prüfung.
Ihre Privatsphäre ist uns wichtig. Aus diesem Grund haben wir eine Datenschutzrichtlinie entwickelt, die beschreibt, wie wir Ihre Informationen verwenden und speichern. Bitte lesen Sie unsere Datenschutzerklärung und lassen Sie uns wissen, wenn Sie Fragen haben.
Erhebung und Verwendung personenbezogener Daten
Personenbezogene Daten sind Daten, mit denen eine bestimmte Person identifiziert oder kontaktiert werden kann.
Sie können jederzeit um die Angabe Ihrer persönlichen Daten gebeten werden, wenn Sie uns kontaktieren.
Im Folgenden finden Sie einige Beispiele für die Arten von personenbezogenen Daten, die wir möglicherweise erfassen, und wie wir diese Daten möglicherweise verwenden.
Welche personenbezogenen Daten wir erheben:
- Wenn Sie eine Bewerbung auf der Website einreichen, erfassen wir möglicherweise verschiedene Informationen, einschließlich Ihres Namens, Ihrer Telefonnummer, Ihrer E-Mail-Adresse usw.
Wie wir Ihre personenbezogenen Daten verwenden:
- Die von uns gesammelten personenbezogenen Daten ermöglichen es uns, Sie zu kontaktieren und Sie über einzigartige Angebote, Werbeaktionen und andere Veranstaltungen und bevorstehende Veranstaltungen zu informieren.
- Von Zeit zu Zeit können wir Ihre personenbezogenen Daten verwenden, um Ihnen wichtige Mitteilungen und Mitteilungen zu senden.
- Wir können personenbezogene Daten auch für interne Zwecke verwenden, z. B. zur Durchführung von Audits, Datenanalysen und verschiedenen Recherchen, um die von uns angebotenen Dienstleistungen zu verbessern und Ihnen Empfehlungen zu unseren Dienstleistungen zu geben.
- Wenn Sie an einer Verlosung, einem Wettbewerb oder einem ähnlichen Anreiz teilnehmen, können wir die von Ihnen bereitgestellten Informationen verwenden, um solche Programme zu verwalten.
Weitergabe an Dritte
Wir geben die von Ihnen erhaltenen Informationen nicht an Dritte weiter.
Ausnahmen:
- Für den Fall, dass es erforderlich ist - in Übereinstimmung mit dem Gesetz, der gerichtlichen Anordnung, in Gerichtsverfahren und / oder aufgrund öffentlicher Anfragen oder Anfragen staatlicher Stellen im Hoheitsgebiet der Russischen Föderation - Ihre personenbezogenen Daten offenzulegen. Wir können auch Informationen über Sie offenlegen, wenn wir feststellen, dass eine solche Offenlegung aus Gründen der Sicherheit, der Strafverfolgung oder aus anderen Gründen des öffentlichen Interesses notwendig oder angemessen ist.
- Im Falle einer Umstrukturierung, Fusion oder eines Verkaufs können wir die von uns erfassten personenbezogenen Daten an den entsprechenden Drittnachfolger übertragen.
Schutz personenbezogener Daten
Wir treffen Vorkehrungen – einschließlich administrativer, technischer und physischer – zum Schutz Ihrer personenbezogenen Daten vor Verlust, Diebstahl und Missbrauch sowie vor unbefugtem Zugriff, Offenlegung, Änderung und Zerstörung.
Wahrung Ihrer Privatsphäre auf Unternehmensebene
Um sicherzustellen, dass Ihre personenbezogenen Daten sicher sind, kommunizieren wir Datenschutz- und Sicherheitspraktiken an unsere Mitarbeiter und setzen Datenschutzpraktiken strikt durch.