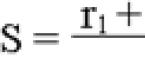Числа Фибоначчи.

При решении многих комбинаторных задач применяют метод сведения данной задачи к задаче касающегося меньшего числа элементов. Например, можно вывести формулу для числа перестановок:

Отсюда видно, что всегда может быть сведён к факториалу от меньшего числа.

Хорошей иллюстрацией к построению рекуррентных соотношений является задача Фибоначчи. В своей книге в 1202 г. итальянский математик Фибоначчи привел следующую задачу. Пара кроликов приносит приплод раз в месяц двух крольчат (самку и самца), причём новорождённые крольчата через два месяца после рождения сами приносят приплод. Сколько кроликов появится через год, если в начале была одна пара кроликов.

Из условия задачи следует, что через месяц будет две пары кроликов, через два месяца приплод даст только первая пара кроликов, появившихся два месяца назад, поэтому всего будет 3 пары кроликов. Ещё через месяц будет уже 5 пар. И так далее.

Обозначим через количество пар кроликов по истечении месяцев с начала года. Тогда через месяц количество пар кроликов можно найти по формуле:

Эта зависимость называется рекуррентным соотношением . Слово «рекурсия» означает возврат назад (в нашем случае – возврат к предыдущим результатам).

По условию, и , тогда по соотношению имеем: , , и т.д., .

Определение 1: Числа называются числами Фибоначчи . Это – известная в математике последовательность чисел:

1, 1, 2, 3, 5, 8, 13, 21, ...

В этой последовательности каждое последующее число является суммой двух предыдущих чисел. И в рекуррентном соотношении также последующий член находится как сумма двух предыдущих членов.

Установим связь между числами Фибоначчи и комбинаторной задачей. Пусть требуется найти число - последовательностей, состоящих из нулей и единиц, в которых никакие две единицы не стоят подряд.

Возьмем любую такую последовательность и сопоставим ей пару кроликов по следующему правилу: единицам соответствуют месяцы появления на свет одной из пар «предков» данной пары (включая и исходную), а нулями – все остальные месяцы. Например, последовательность устанавливает такую «генеалогию» – сама пара появилась в конце 11-го месяца, ее родители в конце 7-го месяца, «дед» – в конце 5-го месяца, и «прадед» в конце 2-го месяца. Первоначальная пара шифруется последовательностью . Ни в одной последовательности две единицы не могут стоять подряд – только что появившаяся пара не может принести приплод через месяц. Очевидно, различным последовательностям отвечают различные пары и обратно.

Таким образом, число последовательностей с указанными свойствами, равно .

Теорема 1: Число находится как сумма биномиальных коэффициентов:. Если – нечетно, то . Если – четно, то . Иначе: – целая часть числа .

Доказательство: В самом деле, - число всех последовательностей из 0 и 1, в которых никакие две единицы не стоят рядом. Число таких последовательностей, содержащих ровно единиц и нулей, равно , при этом , тогда изменяется от 0 до . Применяя правило суммы, получаем данную сумму.

Это равенство можно доказать иначе. Обозначим:

Из равенства , следует, что . Кроме этого, ясно, что и . Так как обе последовательности и удовлетворяют рекуррентному соотношению , то , и .

Определение 2: Рекуррентное соотношение имеет порядок , если оно позволяет вычислять через предыдущих членов последовательности: .

Например, – рекуррентное соотношение второго порядка, а рекуррентное соотношение 3-го порядка. Соотношение Фибоначчи является соотношением второго порядка.

Определение 3:Решением рекуррентного соотношения является последовательность, удовлетворяющая этому соотношению.

Если задано рекуррентное соотношение ‑ го порядка, то ему удовлетворяют бесконечно много последовательностей, т.к. первые элементов можно задать произвольно. Но если первые элементов заданы, то остальные члены определяются однозначно.

Например, соотношению Фибоначчи кроме рассмотренной выше последовательности 1, 1, 2, 3, 5, 8, 13, 21, ..., могут удовлетворять также и другие последовательности. К примеру, последовательность 2, 2, 4, 8, 12,... строится по тому же принципу. Но если задать начальные члены (их в последовательности Фибоначчи - 2), то решение определяется однозначно. Начальных членов берут столько, каков порядок соотношения.

По известным рекуррентным соотношениям и начальным членам можно выписывать члены последовательности один за другим и таким путем мы можем получить любой её член. Но во многих случаях, нам не нужны все предыдущие члены, а необходим один определенный член. В этом случае удобнее иметь формулу ‑ го члена последовательности.

Мы будем говорить, что некоторая последовательность является решением данного рекуррентного соотношения, если при подстановке этой последовательности соотношение тождественно выполняется.

Например, последовательность является одним из решений соотношения: . Это легко проверить обычной подстановкой.

Определение 4: Решение рекуррентного соотношения ‑ го порядка называется общим , если оно зависит от произвольных постоянных , меняя которые, можно получить любое решение данного соотношения.

Например, для соотношения общим решение будет .

В самом деле, легко проверяется, что оно будет решением нашего соотношения. Покажем, что любое решение можно получить в таком виде. Пусть и – произвольны.

Тогда найдутся такие и , что

Очевидно, для любых , система уравнений имеет единственное решение.

Определение 5: Рекуррентное соотношение называется линейным , если оно записывается в виде:

где - числовые коэффициенты.

Для решения произвольных рекуррентных соотношений общих правил, вообще говоря, нет. Однако для решения линейных рекуррентных соотношений есть общие правила решения.

Рассмотрим сначала соотношение 2-го порядка .

Решение этого соотношения основано на следующих утверждениях.

Теорема 2: Если и - являются решением данного рекуррентного соотношения 2-го порядка, то для любых чисел и последовательность также является решением этого соотношения.

Теорема 3: Если число является корнем квадратного уравнения , то последовательность является решением рекуррентного соотношения .

Из теорем 2, 3 вытекает следующее правило решения линейных рекуррентных соотношений 2-го порядка.

Пусть дано рекуррентное соотношение .

1) Составим квадратное уравнение , которое называется характеристическим для данного соотношения. Найдём все корни этого уравнения (даже кратные и комплексные).

2) Составим общее решение рекуррентного соотношения. Его структура зависит от вида корней (одинаковые они или различные).

а) Если это соотношение имеет два различных корня и , то общее решение соотношения имеет вид .

Действительно, из теорем 2, 3 следует, что - решение и система уравнений

Имеет единое решение, т.к. при условии .

Например, для чисел Фибоначчи, имеем . Характеристическое уравнение имеет вид: . Решая последнее уравнение, получим корни:, .

Если все корни характеристического уравнения различны, то общее решение имеет вид: .

Если же, например, , то этому корню соответствуют решения:

данного рекуррентного соотношения. В общем решении этому корню соответствует часть .

Например , решая рекуррентное соотношение:

составляем характеристическое уравнение вида: .

Его корни , . Поэтому общее решение есть.

При большом объеме совокупности данных наблюдения х конечные методы решения уравнения правдоподобия приводят к значительным вычислительным трудностям, связанным с необходимостью запомина­ния большого числа исходных данных и промежуточных результатов вычислений. В связи с этим особый интерес представляют рекуррентные методы, в которых оценка максимального правдоподобия вычисляется по шагам с постепенно увеличивающейся точностью, причем каждый шаг связан с получением новых данных наблюдения, а рекуррентная проце­дура строится так, чтобы хранить в памяти по возможности наименьшее количество данных от предыдущих шагов. Дополнительным и весьма существенным с практической точки зрения преимуществом рекуррент­ных методов является готовность к выдаче результата на любом про­межуточном шаге.

Это обусловливает целесообразность применения рекуррентных ме­тодов даже в тех случаях, если удается получить точное решение урав­нения максимального правдоподобия конечным методом, и делает их еще более ценными, когда невозможно найти точное аналитическое вы­ражение для оценки максимального правдоподобия.

Пусть совокупность данных наблюдения представляет собой по­следовательность для описания которой введем вектор . (Как всегда, каждая его компонента , в свою очередь, может быть вектором, отрезком случайного процесса и т. д.). Пусть - функция правдоподобия, а

ее логарифм. Последний всегда можно представить в виде

Логарифм функции правдоподобия для совокупности данных наблю­дения без последнего значения, а

Логарифм условной плотности вероятности значения при заданных значениях и .

Представление (7,5.16) для логарифма функции правдоподобия яв­ляется основой для получения рекуррентной процедуры вычисления оценки максимального правдоподобия. Рассмотрим регулярный случай. При этом оценка максимального правдоподобия может быть найдена как решение уравнения

которое отличается от (7.1.6) только введением индекса п у логарифма функции правдоподобия.

Обозначим решение этого уравнения через подчеркнув тем са­мым, что эта оценка получена по совокупности данных наблюдения . Аналогично обозначим через решение уравнения- оценку максимального правдоподобия, полученную по совокупности данных .

Уравнение (7.5.19) можно переписать с учетом (7.5.16) в следующем виде:

Разложим левую часть (7.5.20) в ряд Тейлора в окрестности точки . При этом

(7.5.22)

Вектор градиента функции в точке ; слагаемое обращается в нуль благодаря тому, что , является решением уравнения правдоподобия для предыдущего (п - 1)-го шага:

Симметричная матрица вторых производных логарифма функции правдоподобия в точке , взятая с обратным знаком, аненапи­санные члены разложения имеют квадратичный и более высокий поря­док малости относительно разности . Пренебрегая этими по­следними, получаем следующее приближенное решение уравнения ма­ксимального правдоподобия:

где - матрица, обратная .

Это решение представлено в форме рекуррентного соотношения, определяющего очередное значение оценки через оценку на предыдущем шаге и поправку , зависящую от имеющихся данных наблюдения непосредственно и через предыдущую оценку. Поправка формируется как произведение градиента логарифма условной плотно­сти вероятности вновь полученного значения х n в точке , равной предыдущей оценке, на весовую матрицу . По­следняя определяется выражением (7.5.23) и также зависит от оценки на предыдущем шаге, а ее зависимость от новых данных наблюдения целиком определяется видом логарифма условной плотности веро­ятности .

По форме соотношение (7.5.24) очень похоже на (7.5.8), реализую­щее итеративный способ вычисления оценки максимального правдоподо­бия по методу Ньютона. Однако на самом деле они существенно отли­чаются друг от друга. В (7.5.8) поправка к предыдущему значению оцен­ки определяется величиной градиента логарифма всей функции правдо­подобия, который всегда зависит от всех имеющихся данных наблюде­ния , что требует запоминания всей этой совокупности. В соответствии с (7.5.24) поправка к определяется величиной гра­диента , который благодаря свойствам условной плотности вероятностифактически зависит только от тех значений (), которые находятся в сильной статистической связи с х n . Это различие является следствием специального выбора предыдущего приближения как оценки максимального правдоподобия, найденной по уменьшенной на одно значение совокупности данных наблюдения , и особенно ярко проявляется при независимых значениях (). В этом последнем случае

благодаря чему зависит только от и х n , а градиент - только от предыдущего значения оценки и вновь полученных на п- мшаге данных наблюдения . Поэтому при незави­симых значениях для формирования вектора не требуется запо­минать с предыдущего шага никакой иной информации, кроме значения оценки .

Аналогично, в случае марковской последовательности данных на­блюдения, то есть при

вектор зависит только от , текущего и одного предыдущего значения .В этом случае для вычисления требуется запомнить с предыдущего шага, помимо значения , еще только значение , но не всю совокупность данных наблюдения, как в ите­ративной процедуре. В общем случае для вычисления может потребоваться запоминание большего числа предыдущих значений (), однако из-за необходимости учета только тех значе­ний , которые статистически зависимы с , это число практически всегда меньше полного объема совокупности данных наблюдения . Так, если вектор описывает временную последователь­ность, то количество подлежащих запоминанию членов этой последова­тельности определяется временем ее корреляции, а относительная их доля убывает обратно пропорционально n , как и в случае независимых значений .

Рассмотрим теперь структуру весовой матрицы , входящей в ре­куррентное соотношение (7.5.24). Согласно определению (7.5.23), из-за наличия слагаемого она, вообще говоря, зависит от всех значений даже при независимых значениях , что ли­шает рекуррентное соотношение (7.5.24) преимуществ, связанных с воз­можным сокращением количества запоминаемых с предыдущего шага данных. Существует несколько способов приближенного вычисления ма­трицы , которые устраняют этот недостаток.

Первый из них основан на более последовательном использовании основного предположения о малом различии двух очередных значений оценки и , которое является основой для получения рекур­рентного соотношения (7.5.24). Это позволяет получить аналогичное ре­куррентное соотношение для весовой матрицы .Действительно, используя малость из (7.5.23), имеем

Введя обозначение

из (7.5.24) и (7.5.25) получим систему рекуррентных соотношений для вектора и весовой матрицы

Эта система совместно с начальными значениями и полностью определяет значение оценки на любом шаге, требуя на каждом из них вычисления только градиента и матрицы вторых производных от логарифма условной плотности вероятности для текущего наблюдаемого значения . Начальные значе­ния выбираются с учетом имеющихся априорных данных о возможных значениях и диапазоне изменения параметров , а при полном отсутст­вии этих данных принимаются нулевыми (,).

При независимых значениях система рекуррентных соотношений (7.5.27), очевидно, описывает многомерный (размерности ) марковский случайный процесс, компонента которого сходит­ся к истинному значению параметра , а компонента сходится к ин­формационной матрице Фишера (7.3.8), где - истинное значение оцениваемого параметра, и неограниченно увеличивается с ростом п. Аналогичные свойства сходимости система (7.5.27) имеет и при более общихусловиях, если последовательность явля­ется эргодической.

Второй из упомянутых способов основан на замене матрицы вторых производных от логарифма функции правдоподобия ее матема­тическим ожиданием - информационной матрицей Фишера, которая с учетом (7.5.16) может быть записана в виде:

где аналогично (7.5.26)

Заменяя в (7.5.24) матрицу матрицей , получаем ре­куррентное соотношение

для приближенного вычисления оценок максимального правдоподобия, предложенное Сакрисоном (в оригинале для независимых одина­ково распределенных , когда и . Это рекуррентное соотношение проще системы (7.5.27), поскольку оптимальная весовая матрица заменена ее мате­матическим ожиданием, и для ее нахождения не требуются имеющиеся данные наблюдения, кроме тех, которые сконцентрированы в значении оценки . В то же время очевидно, что подобная замена означает необходимость выполнения дополнительного по сравнению с (7.5.27) требования близости матрицы вторых производных к своему математи­ческому ожиданию.

Если плотность распределения вероятности и матри­ца меняются от шага к шагу, прямое нахождение на каждом шаге может потребовать слишком большого числа вычисле­ний. При этом за счет дополнительного уменьшения точности ре­зультатов, определяемого неравенством нулю малых разностей , можно перейти к рекуррентному вычислению приближен­ного значения матрицы . Возвращаясь к прежнему обозначе­нию для этого приближенного значения, получаем еще одну систему рекуррентных соотношений

Математическое ожидание матрицы (информационная матри­ца Фишера для одного наблюдения ), взятое в точке . Эта система отличается от (7.5.27) тем, что во втором из рекуррентных соот­ношений (7.5.31) не участвуют непосредственно данные наблюдения .

Любая из рассмотренных выше систем рекуррентных соотношений является совершенно точной, если функция квадратично зависит от , и дополнительно матрица вторых производных не зависит от . Фактически это соответствует случаю независимых нормально рас­пределенных (не обязательно одинаково) значений с неизвестным математическим ожиданием , которое и представляет собой оценивае­мый параметр.

Система рекуррентных соотношений (7.5.24) дает точное решение уравнения максимального правдоподобия в гораздо более широких условиях при единственном требовании, чтобы функция квадра­тично зависела от . При этом зависимость от произвольна, что соответствует широкому классу распределений вероятности совокуп­ности как с независимыми, так и с зависимыми значениями.

Наряду с рассмотренными общими способами существует еще ряд методов выбора матрицы весовых коэффициентов в рекуррентном соотношении (7.5.24), приспособленных к тем или иным конкретным ограничениям. Простейшим из них является выбор в виде диагональной матрицы, так что , (I - единичная матрица), где - убывающая последовательность чис­ловых коэффициентов, выбираемая независимо от свойств функции правдоподобия так же, как в процедуре стохастической аппроксимации Робинса - Монро, которая будет рассмотрена в следующих главах.

Стоит отметить, что любые итерационные или рекуррентные про­цедуры нахождения оценок максимального правдоподобия в общем случае являются приближенными. Поэтому, вообще говоря, для оценок, получающихся в результате применения этих процедур, состоятельность, асимптотическую эффективность и асимптотическую нормальность нуж­но доказывать заново. Для итеративных процедур необходимые свой­ства оценок гарантируются тем, что в принципе такие процедуры при соответствующем числе итераций дают решение уравнения правдоподо­бия с любой наперед заданной точностью. Для рекуррентных процедур типа (7.5.27), (7.5.30), (7.5.31) и других имеются специальные доказа­тельства. При этом, помимо требования регулярности, предъявляются некоторые дополнительные требования:

На поведение функции (7.2.2) при различных значениях ||, для достижения с помощью рекуррентной процедуры глобаль­ного максимума этой функции в точке , соответствующей истинно­му значению параметра;

На порядок роста вторых моментов производных логарифма функции правдоподобия при больших по модулю значениях . Эти тре­бования являются следствием более общих усло­вий сходимости в точку всех или части компонент марковского случай­ного процесса, к которому приводит та или иная рекуррентная про­цедура.

В заключение отметим также, что в том случае, когда существует точное решение уравнения максимального правдоподобия, оно практиче­ски всегда может быть представлено в рекуррентном виде. Приведем два простых разнородных примера. Так, элементарная оценка неизвест­ного математического ожидания нормальной случайной величины по совокупности n ее выборочных значений в виде арифме­тического среднего

является оценкой максимального правдоподобия и может быть пред­ставлена в рекуррентном виде:

что является самым простым частным случаем (7.5.30) при

Другой пример - это нерегулярная оценка максимального правдо­подобия для параметра - ширины прямоугольного распределения – из (7.4.2), которая также может быть определена рекуррентным соот­ношением

с начальным условием . Это рекуррентное соотношение уже дру­гого типа: его правую часть нельзя представить в виде суммы предыду­щей оценки и малой поправки, что является следствием нерегулярности этого примера; однако оно обладает всеми преимуществами рекуррент­ного подхода: требует запоминания с предыдущего шага всего одного числа - оценки - и резко сокращает перебор до одного сравнения свместо сравнения всех значений .

Приведенные примеры иллюстрируют преимущества рекуррентных методов даже в том случае, когда уравнение максимального правдопо­добия допускает точное решение, ибо простота аналитического пред­ставления результата не тождественна вычислительной простоте его по­лучения.

7.5.3. Переход к непрерывному времени. Дифференциальные уравнения для оценок максимального правдоподобия

Рассмотрим теперь специальный случай, когда имеющиеся данные наблюдения х описываются не совокупностью выборочных точек , а представляют собой отрезок реализации некоторого процесса , зависящего от параметров , заданный на интервале , при­чем длина этого интервала может увеличиваться при наблюдении (мо­мент времени t является переменным).

Для статистического описания данных наблюдения в этом случае вводится функционал отношения правдоподобия, представляющий собой предел при , maxотношения плотности распределе­ния вероятности совокупности значений при произ­вольно заданном значении к аналогичной плотности вероятности при некотором фиксированном значении , а в некоторых случаях, когда допускает представление , где - случай­ный процесс, не зависящий от , к плотности вероятности совокупности значений при условии, что . Использование функционала отношения правдоподобия позволяет исключить формальные труд­ности определения плотности вероятности, возникающие при переходе к непрерывному времени.

Логарифм функционала отношения правдоподобия может быть представлен в виде

где - некоторый функционал процесса на интервале . В некоторых случаях функционал вырождается в функ­цию, зависящую только от значения . Так, если

где - известная функция времени и параметров , а - дельта-коррелированный случайный процесс («белый» шум) со спек­тральной плотностью N o ,то, выбирая в качестве знаменателя отношения правдоподобия распределения вероятности х при , будем иметь

Пусть - оценка максимального правдоподобия параметра , построенная по реализации процесса на интервале ,то есть решение уравнения максимального правдоподобия

Дифференцируя левую часть этого уравнения по времени, получаем

Вводя обозначения

и решая уравнение (7.5.42) относительно , получаем диффе­ренциальное уравнение для оценки максимального правдоподобия

Матрица , в свою очередь, согласно (7.5.37) определяется диффе­ренциальным уравнением

Так же, как в дискретном случае, матрица в (7.5.45), (7.5.47) мо­жет быть заменена своим математическим ожиданием - информационной матрицей Фишера при значении , а диф­ференциальное уравнение (7.5.46) для весовой матрицы - урав­нением

где аналогично дискретному случаю

Математическое ожидание матрицы вторых производных .

Совокупность дифференциальных уравнений (7.5.45), (7.5.46) или (7.5.45), (7.5.48) совместно с начальными условиями, относительно вы­бора которых остается в силе все сказанное для дискретного случая, полностью определяет оценку максимального правдоподобия для любого момента времени. Эта совокупность может быть смоделирована с помощью соответствующих, вообще говоря, нелинейных аналоговых устройств или при подходящей дискретизации по времени решена с по­мощью ЭВМ. Отметим в заключение одну из модификаций этих урав­нений, позволяющую избежать необходимости обращения матрицы .

Вводя обозначение

, где I

и дифференцируя по времени соотношение , где I - единич­ная матрица, получаем с помощью (7.5.46) дифференциальное уравне­ние, определяющее непосредственно матрицу :

(и аналогично при замене на ), которое совместно с уравнением (7.5.45)

определяет оценку , не требуя обращения матриц. При этом имеет место переход от простейшего линейного дифференциального уравнения (7.5.46) к нелинейному относительно дифференциальному уравне­нию (7.5.51) типа Риккати.

Общим решением рекуррентного соотношения (1) называется множество всех последовательностей, удовлетворяющих этому соотношению.

Частным решением соотношения (1) называется одна из последовательностей, удовлетворяющих этому соотношению.

Пример 1¢. Последовательность a n =a 0 +nd a n =a n - 1 +d . Это - формула общего члена арифметической прогрессии с разностью d и с начальным членом прогрессии a 0 .

Пример 2¢. Последовательность b n =b 0 ×q n является общим решением соотношения b n =b n - 1 ×q . Это - формула общего члена геометрической прогрессии со знаменателем q ¹0 и с начальным членом прогрессии b 0 .

Пример 3¢. Так называемая формула Бине j n =является частным решением соотношения j n =j n - 2 +j n - 1 при j 0 =j 1 =1.

Так как простые корни x 1 ,…,x k попарно различные, то D¹0. Значит, система (5) имеет (единственное) решение.

Задача 1. Найти общий член геометрической прогрессии по формуле (4).

Решение b n =qb n - 1 имеет вид . Поэтому .

Задача 2. Найти общее решение соотношения Фибоначчи a n + 2 =a n +a n + 1 .

Решение . Характеристический многочлен рекуррентного соотношения a n + 2 =a n +a n + 1 имеет вид . Поэтому .

Приведем без доказательства следующее обобщение теоремы 1.

Теорема 2 . Пусть характеристический многочлен однородного линейного рекуррентного соотношения (3) имеет k корней: a 1 кратности , …, a k кратности , , . Тогда общее решение рекуррентного соотношения (3) имеет следующий вид:

Задача 3. Найти общее решение соотношения .

Решение. Характеристический многочлен имеет корень 2 кратности 3. Поэтому .

Замечание . Общее решение неоднородного линейного соотношения (2) можно найти как сумму общего решения однородного линейного соотношения (3) и частного решения неоднородного линейного соотношения (2).

4. Производящие функции. Формальный ряд a 0 +a 1 x +a 2 x 2 +…+a k x k +… называется производящей функцией последовательности a 0 ,a 1 ,a 2 ,…,a k ,…

Производящая функция является или сходящимся рядом, или расходящимся рядом. Два расходящихся ряда могут быть равны как функции, но быть производящимися функциями различных последовательностей. Например, ряды 1+2x +2 2 x 2 +…+2 k x k +… и 1+3x +3 2 x 2 +…+3 k x k +… определяют одну и ту же функцию (равную 1 в точке x =1, неопределенную в точках x >1), но являются производящими функциями различных последовательностей.

Свойства производящих функций последовательностей:

сумма (разность) производящих функций последовательностей a n и b n равна производящей функции сумме (разности) последовательностей a n +b n ;

произведение производящих функций последовательностей a n и b n является производящей функцией свёртки последовательностей a n и b n :

c n =a 0 b n +a 1 b n - 1 +…+a n - 1 b 1 +a n b 0 .

Пример 1. Функция является производящей для последовательности

Пример 2. Функция является производящей для последовательности 1, 1, 1, …

Транскрипт

1 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Костромской государственный университет имени Н. А. Некрасова Т. Н. Матыцина ДИСКРЕТНАЯ МАТЕМАТИКА РЕШЕНИЕ РЕКУРРЕНТНЫХ СООТНОШЕНИЙ Практикум Кострома 2010

2 ББК я73-5 М348 Печатается по решению редакционно-издательского совета КГУ им. Н. А. Некрасова Рецензент А. В. Чередникова, кандидат физико-математических наук, доцент М348 Матыцина Т. Н. Дискретная математика. Решение рекуррентных соотношений: практикум [Текст] / Т. Н. Матыцина. Кострома: КГУ им. Н. А. Некрасова, с. Практикум содержит индивидуальные задания для студентов и предназначен для обеспечения самостоятельной работы по освоению первой части курса «Дискретная математика». Для студентов 2 3 курсов физико-математического факультета, обучающихся по специальностям «Математика» с дополнительной специальностью «Информатика», «Информатика» с дополнительной специальностью «Математика». ББК я73-5 Т. Н. Матыцина, 2010 КГУ им. Н. А. Некрасова,

3 ОГЛАВЛЕНИЕ Введение Методические рекомендации по решению линейных рекуррентных соотношений Основные понятия и определения рекуррентных (возвратных) последовательностей Алгоритмы решения ЛОРС и ЛРС Примеры решения ЛОРС и ЛРС Задачи для самостоятельного решения Задачи для решения ЛОРС и ЛРС Ответы Заключение Библиографический список

4 ВВЕДЕНИЕ Первая часть курса «Дискретная математика», изучаемая студентами 2 3 курсов физико-математического факультета, обучающихся по специальностям «Информатика» с дополнительной специальностью «Математика» (IV семестр) и «Математика» с дополнительной специальностью «Информатика» (V семестр), предполагает решение рекуррентных соотношений. В настоящее издание включены задачи на вычисление однородных и неоднородных линейных рекуррентных соотношений. Поводом для написания практикума послужило то обстоятельство, что у студентов практически нет навыков решения задач по данному курсу. Одной из причин является отсутствие доступного учебника или сборника задач. Задачи из предлагаемого практикума помогут каждому из студентов (индивидуально) разобраться с основными методами и приемами решения задач. С целью более легкого освоения материала в начале пособия рассмотрены все типы задач, предлагаемых для самостоятельного решения. В конце помещен список рекомендуемой литературы, которая поможет глубже изучить данный предмет. Тема «Рекуррентные соотношения» близка к школьному курсу (арифметические и геометрические прогрессии, последовательность квадратов и кубов натуральных чисел, и т. п.), поэтому не требует от студентов предварительного изучения каких-либо других дисциплин. Основы теории рекуррентных соотношений (возвратных последовательностей) были разработаны и опубликованы в 20-х гг. XVIII в. французским математиком А. Муавром и одним из первых по времени членов Петербургской Академии наук швейцарским математиком Д. Бернулли. Развёрнутую теорию дал крупнейший математик XVIII в. 4

5 петербургский академик Л. Эйлер. Из более поздних работ следует выделить изложение теории возвратных последовательностей в курсах исчисления конечных разностей, читанных знаменитыми русскими математиками академиками П. Л. Чебышевым и А. А. Марковым. Рекуррентные соотношения (от латинского слова recurrere возвращаться) играют большую роль в дискретной математике, являясь по существу в некотором смысле дискретным аналогом дифференциальных уравнений. Кроме того, они позволяют сводить данную задачу от параметров к задаче от 1 параметров, потом к задаче от 2 параметров и т. д. Последовательно уменьшая число параметров, можно дойти до задачи, которую уже легко решить. Понятие рекуррентного соотношения (возвратной последовательности) является широким обобщением понятия арифметической или геометрической прогрессии. Как частные случаи оно охватывает также последовательности квадратов или кубов натуральных чисел, последовательности цифр десятичного разложения рационального числа (и вообще любые периодические последовательности), последовательности коэффициентов частного от деления двух многочленов, расположенных по возрастающим степеням х, и т. д. 5

6 1. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ЛИНЕЙНЫХ РЕКУРРЕНТНЫХ СООТНОШЕНИЙ 1.1. Основные понятия и определения рекуррентных (возвратных) последовательностей Будем записывать последовательности в виде a 1, a 2, a 3, a, (1) или, коротко, {a }. Если существует натуральное число k и числа α 1, α 2, α k (действительные или мнимые), такие, что, начиная с некоторого номера и для всех следующих номеров, a +k = α 1 a +k 1 + α 2 a +k α k a, (k 1), (2) то последовательность (1) называется рекуррентной (возвратной) последовательностью порядка k, а соотношение (2) рекуррентным (возвратным) уравнением порядка k. Таким образом, рекуррентная последовательность характеризуется тем, что каждый её член (начиная с некоторого из них) выражается через одно и то же количество k непосредственно предшествующих ему членов по формуле (2). Само название «рекуррентная» (а также возвратная) употребляется именно потому, что здесь для вычисления последующего члена возвращаются к предшествующим членам. Приведём несколько примеров рекуррентных последовательностей. Пример 1. Геометрическая прогрессия. Пусть имеем геометрическую прогрессию: a 1 = α, a 2 = α q, a 3 = α q 2, a = α q 1, ; (3) для неё уравнение (2) принимает вид: a +1 = q a. (4) 6

7 Здесь k = 1 и α 1 = q. Таким образом, геометрическая прогрессия является рекуррентной последовательностью первого порядка. Пример 2. Арифметическая прогрессия. В случае арифметической прогрессии a 1 = α, a 2 = α + d, a 3 = α + 2d, a = α + (1)d, имеем a +1 = a + d соотношение, не имеющее вида уравнения (2). Однако если мы рассмотрим два соотношения, написанные для двух соседних значений: a +2 = a +1 + d и a +1 = a + d, то получим из них путём почленного вычитания a +2 a +1 = a +1 a, или a +2 = 2a +1 a уравнение вида (2). Здесь k = 2, α 1 = 2, α 2 = 1. Следовательно, арифметическая прогрессия является рекуррентной последовательностью второго порядка. Пример 3. Рассмотрим старинную задачу Фибоначчи 1 о числе кроликов. В ней требуется определить число пар зрелых кроликов, образовавшихся от одной пары в течение года, если известно, что каждая зрелая пара кроликов ежемесячно рождает новую пару, причём новорождённые достигают полной зрелости в течение месяца. В этой задаче интересен отнюдь не результат, получить который совсем нетрудно, но последовательность, члены которой выражают общее число зрелых пар кроликов в начальный момент (a 1) через месяц (a 2), через два месяца (a 3) и, вообще, через месяцев (a +1). Очевидно, что a 1 = 1. Через месяц прибавится пара новорождённых, но число зрелых пар будет прежнее: a 2 = 1. Через два месяца крольчата достигнут зрелости и общее число зрелых пар будет равно двум: a 3 = 2. Пусть мы вычислили уже количество 1 Фибоначчи, или Леонардо Пизанский, итальянский средневековый математик (около 1200 г.) оставил после себя книгу «Об абаке», содержащую обширные арифметические и алгебраические сведения, заимствованные у народов Средней Азии и византийцев и творчески им переработанные и развитые. 7

8 зрелых пар через 1 месяцев a и через месяцев a +1. Так как к этому времени a ранее имевшихся зрелых пар дадут ещё a пар приплода, то через + 1 месяцев общее число зрелых пар будет: a +2 = a +1 + a. (6) Отсюда a 4 = a 3 + a 2 = 3, a 5 = a 4 + a 3 = 5, a 6 = a 5 + a 4 = 8, a 7 = a 6 + a 5 = 13,. Мы получили, таким образом, последовательность a 1 = 1, a 2 = 1, a 3 = 2, a 4 = 3, a 5 = 5, a 6 = 8, a 7 = 13, a 13 = 233, (7) в которой каждый последующий член равен сумме двух предыдущих. Последовательность эта называется последовательностью Фибоначчи, а члены её числами Фибоначчи. Уравнение (6) показывает, что последовательность Фибоначчи есть рекуррентная последовательность второго порядка. Пример 4. В качестве следующего примера рассмотрим последовательность квадратов натуральных чисел: a 1 = 1 2, a 2 = 2 2, a 3 = 3 2, a = 2,. (8) Здесь a +1 = (+ 1) 2 = и, следовательно, a +1 = a (9) Увеличивая на единицу, получим: a +2 = a (10) И, следовательно (вычитая почленно (9) из (10)), a +2 a +1 = a +1 a + 2, или a +2 = 2a +1 a + 2. (11) Увеличивая в равенстве (11) на единицу, будем иметь: a +3 = 2a +2 a ; (12) откуда (вычитая почленно (11) из (12)) a +3 a +2 = 2a +2 3a +1 + a, 8

9 или a +3 = 3a +2 3a +1 + a. (13) Мы получили рекуррентное уравнение третьего порядка. Следовательно, последовательность (8) есть рекуррентная последовательность третьего порядка. Пример 5. Рассмотрим последовательность кубов натуральных чисел: a 1 = 1 3, a 2 = 2 3, a 3 = 3 3, a = 3,. (14) Подобным же образом, как в примере 4, можно убедиться в том, что последовательность кубов натуральных чисел есть рекуррентная последовательность четвёртого порядка. Члены её удовлетворяют уравнению a +4 = 4a +3 6a a +1 a. (15) В случае простейших рекуррентных последовательностей, например арифметической и геометрической прогрессий, последовательности квадратов или кубов натуральных чисел, мы можем находить любой член последовательности, не прибегая к вычислению предшествующих членов. В случае же последовательности чисел Фибоначчи мы, на первый взгляд, не имеем возможности для этого и, чтобы вычислить тринадцатое число Фибоначчи a 13, находим предварительно, один за другим, все предшествующие члены (пользуясь уравнением a +2 = a +1 + a (6)): a 1 = 1, a 2 = 1, a 3 = 2, a 4 = 3, a 5 = 5, a 6 = 8, a 7 = 13, a 8 = 21, a 9 = 34, a 10 = 55, a 11 = 89, a 12 = 144, a 13 = 233. В ходе детального исследования структуры членов рекуррентной последовательности можно получить формулы, позволяющие вычислить в самом общем случае любой член рекуррентной последовательности, не прибегая к вычислению предшествующих членов. Другими словами, следующая задача состоит в том, чтобы отыскать формулу -го члена последовательности, зависящую только от номера. 9

10 Рекуррентное соотношение в общем случае может быть записано в виде a +k = F(, a +k 1, a +k 2, a), где F функция от k + 1 переменной, а число k называют порядком соотношения. Решением рекуррентного соотношения называется числовая последовательность b 1, b 2, b 3, b, для которой выполняется равенство: b +k = F(, b +k 1, b +k 2, b) при любом = 0, 1, 2,. Вообще говоря, произвольное рекуррентное соотношение имеет бесконечно много решений. Например, если рассмотреть рекуррентное соотношение второго порядка a +2 = a +1 + a, то ему, кроме последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34,..., характеризующейся тем, что здесь a 1 = a 2 = 1, удовлетворяет ещё бесконечное множество других последовательностей, получающихся при различном выборе значений a 1 и a 2. Так, например, при a 1 = 3 и a 2 = 1 получаем последовательность: 3, 1, 2, 1, 3, 4, 7, 11, 18, 29,. Чтобы однозначно определить решение рекуррентного соотношения, необходимо задать начальные условия (начальных условий должно быть ровно столько, каков порядок рекуррентного соотношения). Решить рекуррентное соотношение значит найти формулу -го члена последовательности. К сожалению, не существует общего метода решения произвольных рекуррентных соотношений. Исключением является класс так называемых линейных рекуррентных соотношений с постоянными коэффициентами. Рекуррентное соотношение вида a +k = α 1 a +k 1 + α 2 a +k α k a, где a i некоторые числа, i = 1, 2, k, называется линейным однородным рекуррентным соотношением (ЛОРС) с постоянными коэффициентами порядка k. 10

11 Рекуррентное соотношение вида a +k = α 1 a +k 1 + α 2 a +k α k a + f(), где a i некоторые числа, i = 1, 2, k, f() 0 функция от, называется линейным рекуррентным соотношением (ЛРС) с постоянными коэффициентами порядка k Алгоритмы решения ЛОРС и ЛРС Алгоритм решения ЛОРС. Имеем ЛОРС: a +k = α 1 a +k 1 + α 2 a +k α k a. 1 шаг. Каждому ЛОРС порядка k соответствует алгебраическое уравнение степени k с теми же коэффициентами, и оно называется характеристическим уравнением ЛОРС. Составляем характеристическое уравнение x k = α 1 x k 1 + α 2 x k α k x 0 и находим его корни x i, где i = 1, k. 2 шаг. Если x i корни кратности 1 (т. е. все различны между собой), то общее решение ЛОРС имеет вид: a = c 1 (x 1) + c 2 (x 2) + c 3 (x 3) + + c k (x k) = c i x i Если x i корни кратности r i, то общее решение ЛОРС имеет вид k a = i= 1 (c 1 2 ri 1 i1 + ci2 + ci cir) (например, если корень x кратности 2, то a = (c 1 + c 2) x). i x i k i= 1 3 шаг. Коэффициенты c i находятся с помощью начальных условий. 11

12 Алгоритм решения ЛРС. Имеем ЛРС: a +k = α 1 a +k 1 + α 2 a +k α k a + f(). Функцию f() можно представить в виде R m () λ, где R m () многочлен степени m от переменной. В самом деле, например: f() = 10 3= (10 3)1 = R 1 () 1, или f() = = (2 + 3) 3 = R 2 () 3. Перепишем ЛРС в виде a +k α 1 a +k 1 α 2 a +k 2 α k a = R m () λ. 1 шаг. Выписываем соответствующий ЛОРС: a +k α 1 a +k 1 α 2 a +k 2 α k a = 0 и находим его общее решение. Для этого составляем характеристическое уравнение x k α 1 x k 1 α 2 x k 2 α k x 0 = 0 и находим его корни x i, где i = 1, k. Пусть, например, x i различные корни, тогда общее решение соответствующего ЛОРС имеет вид: a = c 1 (x 1) + c 2 (x 2) + c 3 (x 3) + + c k (x k). 2 шаг. Находим a частное решение ЛРС: а) если λ не корень характеристического уравнения x k α 1 x k 1 α 2 x k 2 α k = 0, то a = Q m () λ, где Q m () многочлен степени m от переменной; б) если λ корень характеристического уравнения x k α 1 x k 1 α 2 x k 2 α k = 0 кратности r, то a = r Q m () λ, где Q m () многочлен степени m от переменной. Далее, подставляем a в исходное ЛРС и находим коэффициенты в многочлене Q m (). 12

13 3 шаг. Находим общее решение ЛРС, оно представляет собой сумму общего решения соответствующего ЛОРС a и частного решения ЛРС a, то есть a = a + a. Коэффициенты c i находятся с помощью начальных условий Примеры решения ЛОРС и ЛРС Пользуясь приведенным алгоритмом нахождения решения ЛОРС и ЛРС, разберём несколько задач. Задача 1. Найти решение линейного однородного рекуррентного соотношения второго порядка: a +2 = 6 a +1 8 a, a 0 = 3, a 1 = Составляем характеристическое уравнение x 2 = 6 x 8 x 0 и находим его корни. x 2 6x + 8 = 0; x 1 = 2, x 2 = 4 корни различные, следовательно, их кратность равна Находим общее решение ЛОРС: a = c 1 (x 1) + c 2 (x 2) = c c Так как заданы начальные условия, то коэффициенты c 1 и c 2 определяются однозначно. a 0 = c c = c 1 + c 2 = 3; a 1 = c c = 2c 1 + 4c 2 = 4. Получили систему: c1 + c2 = 3, 2c1 + 4c2 = 4. Решая её, найдём коэффициенты: c 1 = 8, c 2 = 5. Таким образом, решение ЛОРС имеет вид a = Задача 2. Найти решение линейного однородного рекуррентного соотношения: 13

14 a +2 = 6 a +1 9 a, a 0 = 5, a 1 = Составляем характеристическое уравнение x 2 = 6x 9 и находим его корни. x 2 6x + 9 = 0; (x 3) 2 = 0; x 1 = x 2 = 3 два корня, при этом x 1 и x 2 совпали, следовательно, кратность корня равна Находим общее решение ЛОРС: a = (c 1 + c 2) (x 1) = (c 1 + c 2) С помощью начальных условий определяем коэффициенты c 1 и c 2: a 0 = (c 1 + c 2 0) 3 0 = c 1 = 5; a 1 = (c 1 + c 2 1) 3 1 = (c 1 + c 2) 3 = 6. Получили систему c1 = 5, c1 + c2 = 2. Решая её, найдём коэффициенты c 1 = 5, c 2 = 3. Таким образом, решение ЛОРС имеет вид: a = (5 3) 3. Замечание. Как известно, корнями квадратного уравнения могут служить рациональные, иррациональные, комплексные числа и т. п. Метод решения линейных рекуррентных соотношений с такими корнями решается аналогично. Задача 3. Найти решение линейного однородного рекуррентного соотношения третьего порядка: a +3 = 3 a a +1 8 a, a 0 = 9, a 1 = 9, a 2 = Составляем характеристическое уравнение x 3 = 3 x x 8 и находим его корни. x 3 3x 2 6x + 8 = 0; (x 1)(x + 2)(x 4) = 0; x 1 = 1, x 2 = 2, x 3 = 4 корни различные, следовательно, их кратность равна Находим общее решение ЛОРС: a = c 1 (x 1) + c 2 (x 2) + c 3 (x 3) = c c 2 (2) + c

15 3. С помощью начальных условий, находим коэффициенты c 1, c 2 и c 3. a 0 = c c 2 (2) 0 + c = c 1 + c 2 + c 3 = 9; a 1 = c c 2 (2) 1 + c = c 1 2c 2 + 4c 3 = 9; a 2 = c c 2 (2) 2 + c = c 1 + 4c c 3 = 9. c1 + c2 + ñ3 = 9, Решая систему c1 2c2 + 4c3 = 9, получим c 1 = 7, c 2 = 4, c 3 = 2. Таким c1 + 4c2 + 16c3 = 9, образом, решение ЛОРС имеет вид: a = (2) 2 4. Задача 4. Найти решение линейного однородного рекуррентного соотношения третьего порядка: a +3 = a a +1 3 a, a 0 = 6, a 1 = 15, a 2 = Составляем характеристическое уравнение x 3 = x 2 + 5x 3 и находим его корни. x 3 + x 2 5x + 3 = 0; (x 1) 2 (x + 3) = 0; x 1 = x 2 = 1 корень кратности 2; x 3 = 3 корень кратности Находим общее решение ЛОРС: a = (c 1 + c 2) (x 1) + c 3 (x 3) = (c 1 + c 2) 1 + c 3 (3). 3. С помощью начальных условий находим коэффициенты c 1, c 2 и c 3. a 0 = (c 1 + c 2 0) c 3 (3) 0 = c 1 + c 3 = 6; a 1 = (c 1 + c 2 1) c 3 (3) 1 = c 1 + c 2 3c 3 = 15; a 2 = (c 1 + c 2 2) c 3 (3) 2 = c 1 + 2c 2 + 9c 3 = 8. c1 + ñ3 = 6, Решая систему c1 + c2 3c3 = 15, получим c 1 = 8, c 2 = 1 и c 3 = 2. Таким c1 + 2c2 + 9c3 = 8, образом, решение ЛОРС имеет вид: a = (8 +) 1 2 (3). 15

16 Задача 5. Найти решение линейного рекуррентного соотношения второго порядка: Перепишем ЛРС в виде a +2 = 18 a a + 128, a 0 = 5, a 1 = 2. a a a = () 1. Выписываем соответствующий ЛОРС: a a a = 0. Составляем характеристическое уравнение и находим его корни. x 2 18x + 81 = 0; (x 9) 2 = 0; x 1 = x 2 = 9 корни характеристического уравнения совпали, следовательно, их кратность равна 2. Тогда общее решение a = (c 1 + c 2) (x 1) = (c 1 + c 2) Находим a частное решение ЛРС. По условию f() = R m () λ = = = R 0 () λ, где R 0 () = 128 многочлен нулевой степени от переменной, а λ = 1 не корень характеристического уравнения соответствующего ЛОРС. Следовательно, a = Q m () λ = Q 0 () 1, где Q 0 () многочлен нулевой степени от переменной, в общем виде Q 0 () = с. Таким образом, a = с 1. Далее, подставляем a в исходное ЛРС () и находим коэффициент с в многочлене Q 0 (): с с с 1 = ; с 18с + 81с = 128; 64с = 128; с = 2. Следовательно, получили a = с 1 = 2 1 = 2. 16

17 3. Находим общее решение ЛРС, оно представляет собой сумму общего решения соответствующего ЛОРС a и частного решения ЛРС a, то есть a = a + a = (c 1 + c 2) Осталось с помощью начальных условий найти коэффициенты c 1, и c 2. a 0 = (c 1 + c 2 0) = c = 5; a 1 = (c 1 + c 2 1) = 9c 1 + 9c = 2; Решая систему c1 + 2 = 5, 9c1 + 9c2 + 2 = 2, получим c 1 = 3, c 2 = 3. Таким образом, решение ЛРС имеет вид: a = (3 3) Задача 6. Найти решение линейного рекуррентного соотношения: a +2 = 10 a a , a 0 = 7, a 1 = 50. Перепишем ЛРС в виде a a a = Выписываем соответствующий ЛОРС: a a a = 0; составляем характеристическое уравнение и находим его корни. x 2 10 x + 25 = 0; (x 5) 2 = 0; x 1 = x 2 = 5 корень кратности 2. Тогда общее решение ЛОРС имеет вид: a = (c 1 + c 2) (x 1) = (c 1 + c 2) Находим a частное решение ЛРС. По условию f() = R m () λ = 50 5 = R 0 () λ, где R 0 () = 50 многочлен нулевой степени от переменной, а λ = 5 совпадает с корнем x 1 кратности 2 характеристического уравнения соответствующего ЛОРС. Следовательно, a = r Q m () λ = = 2 Q 0 () 5, где Q 0 () = с многочлен нулевой степени от переменной. Таким образом, a = 2 с 5. Далее, подставляем a в исходное ЛРС и находим коэффициент с: 17

18 с (+ 2) с (+ 1) с 2 5 = 50 5 (разделим на 5 0); 25с (+ 2) 2 50с (+ 1) с 2 = 50; с () 2с () + с 2 = 2; с = 1. Следовательно, a = 2 с 5 = Выписываем общее решение ЛРС: a = a + a = (c 1 + c 2) С помощью начальных условий находим коэффициенты c 1, и c 2: a 0 = (c 1 + c 2 0) = c 1 = 7; a 1 = (c 1 + c 2 1) = 5c 1 + 5c = 50; Решая систему c1 = 7, c1 + c2 + 1 = 10, получим c 1 = 7, c 2 = 2. Таким образом, решение ЛРС имеет вид: a = (7 + 2) = () 5. Задача 7. Найти решение линейного рекуррентного соотношения: a +2 = 6 a +1 8 a , a 0 = 0, a 1 = 11. Перепишем ЛРС в виде a +2 6 a a = Выписываем соответствующий ЛОРС: a +2 6 a a = 0; составляем характеристическое уравнение и находим его корни. x 2 6x + 8 = 0; x 1 = 2, x 2 = 4 корни кратности равной 1. Тогда общее решение ЛОРС имеет вид a = c 1 (x 1) + c 2 (x 2) = c c Находим a частное решение ЛРС. По условию f() = R m () λ = = (3 + 2) 1 = R 1 () λ, где R 1 () = многочлен первой степени от переменной, а λ = 1 не корень характеристического уравнения соответствующего ЛОРС. Следовательно, a = Q m () λ = Q 1 () 1, где Q 1 () многочлен первой степени от переменной, в общем виде Q 1 () = = a + b. Таким образом, a = (a + b) 1. 18

19 a и b: Далее, подставляем a в исходное ЛРС и находим коэффициенты (a (+ 2) + b) (a (+ 1) + b) (a + b) 1 = 3 + 2; 25с (+ 2) 2 50с (+ 1) с 2 = 3 + 2; 3a + (3b 4a) = Таким образом, получили, что два многочлена равны, а тогда равны соответствующие коэффициенты: 3a = 3, a = 1, 3b 4a = 2 b = 2. Следовательно, a = (a + b) 1 = Выписываем общее решение ЛРС: a = a + a = c c (+ 2). С помощью начальных условий находим коэффициенты c 1, и c 2: a 0 = c c (0 + 2) = 0; a 1 = c c (1 + 2) = 11; Решая систему c1 + c2 = 2, 2c1 + 4c2 = 14, получим c 1 = 3, c 2 = 5. Таким образом, решение ЛРС имеет вид: a = Задача 8. Найти решение линейного рекуррентного соотношения: a +2 = 5 a +1 6 a + (10 4) 2, a 0 = 5, a 1 = 12. Перепишем ЛРС в виде a +2 5 a a = (10 4) Выписываем соответствующий ЛОРС: a +2 5 a a = 0; составляем характеристическое уравнение и находим его корни. x 2 5x + 6 = 0; x 1 = 3, x 2 = 2 корни различные кратности 1. Тогда общее решение ЛОРС имеет вид: a = c 1 (x 1) + c 2 (x 2) = c c

20 2. Находим a частное решение ЛРС. По условию имеем, что f() = = R m () λ = (10 4) 2 = R 1 () λ, где R 1 () = (10 4) многочлен первой степени от переменной, а λ = 2, то есть совпадает с корнем характеристического уравнения соответствующего ЛОРС. Следовательно, a = r Q m () λ = 1 Q 1 () 2, где Q 1 () многочлен первой степени от переменной, в общем виде Q 1 () = a + b. Таким образом, получаем a = = (a + b) 2. Далее, подставляем a в исходное соотношение и находим коэффициенты a и b. (+ 2)(a (+ 2) + b) (+ 1) (a (+ 1) + b) (a + b) 2 = = (10 4) 2. Разделим это уравнение на 2 0: 4(+ 2)(a (+ 2) + b) 10(+ 1) (a (+ 1) + b) + 6(a + b) = 10 4; 4a + (6a 2b) = Таким образом, получили, что два многочлена равны, а тогда равны соответствующие коэффициенты: 4a = 4, a = 1, 6a 2b = 10 b = 2. Следовательно, a = (a + b) 2 = (2) Выписываем общее решение ЛРС, то есть a = a + a = c c (2) 2. С помощью начальных условий находим коэффициенты c 1, и c 2. a 0 = c c (0 2) 2 0 = 5; a 1 = c c (1 2) 2 1 = 12. Решая систему c1 + c2 = 5, 3c1 + 2c2 = 14, получим c 1 = 4, c 2 = 1. Таким образом, решение ЛРС имеет вид: a = (2) 2 = () 2. 20

21 Задача 9. Найти решение линейного рекуррентного соотношения: a +2 = 8 a a , a 0 = 1, a 1 = 7. Перепишем ЛРС в виде a +2 8 a a = () Выписываем соответствующий ЛОРС: a +2 8 a a = 0; составляем характеристическое уравнение и находим его корни. x 2 8 x + 16 = 0; x 1 = x 2 = 4 корни совпали, следовательно, кратность корня равна 2. Тогда общее решение ЛОРС имеет вид: a = (c 1 + c 2) (x 1) = (c 1 + c 2) Находим a частное решение ЛРС. По условию f() = R m () λ = = () 1 = R 2 () λ, где R 2 () = многочлен второй степени от переменной, а λ = 1 не совпадает с корнем характеристического уравнения соответствующего ЛОРС. Следовательно, a = Q m () λ = Q 2 () 1, где Q 2 () многочлен второй степени от переменной, в общем виде Q 2 () = a 2 + b + c. Таким образом, a = = (a 2 + b + c) 1. Далее, подставляем a в исходное соотношение и находим коэффициенты a, b и c. (a (+ 2) 2 + b (+ 2)+ c) (a (+ 1) 2 + b (+ 1) + c) (a b + c) 1 = () 1 ; a(+ 2) 2 + b(+ 2)+ c 8a(+ 1) 2 8b(+ 1) 8c + 16a b + 16c = = ; 9a 2 12a + 9b 4a 6b + 9c = Таким образом, получили, что два многочлена равны, а тогда равны соответствующие коэффициенты: 9a = 9, 12a + 9b = 6, 4a 6b + 9c = 2 a = 1, b = 2, c = 2. 21

22 Следовательно, a = (a 2 + b + c) 1 = Выписываем общее решение ЛРС, то есть a = a + a = (c 1 + c 2) (). С помощью начальных условий, находим коэффициенты c 1, и c 2. a 0 = (c 1 + c 2 0) () = 1; a 1 = (c 1 + c 2 1) () = 7. Решая систему c1 + 2 = 1, 4c1 + 4c2 + 5 = 7, получим c 1 = 1, c 2 = 2. Таким образом, решение ЛРС имеет вид: a = (1 2)

23 2. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 2.1. Задачи для решения ЛОРС и ЛРС Линейные однородные рекуррентные соотношения второго порядка 1. a +2 = 9 a a, a 0 = 2, a 1 = a +2 = 3,5 a +1 2,5 a, a 0 = 3,5, a 1 = a +2 = 8 a a, a 0 = 4, a 1 = a +2 = 2 a a, a 0 = 3, a 1 = i. 5. a +2 = 10 a a, a 0 = 3, a 1 = a +2 = 6 a a, a 0 = 0, a 1 = 2i a +2 = 8 a a, a 0 = 2, a 1 = a +2 = 4 a a, a 0 = 7, a 1 = a +2 = a +1 + a, a 0 = 2, a 1 = a +2 = 8 a a, a 0 = 8, a 1 = a +2 = () a a, a 0 = 7, a 1 = a +2 = 5 a +1 4 a, a 0 = 0, a 1 = a +2 = 2 a +1 5 a, a 0 = 5, a 1 = 6i a +2 = 3 a a, a 0 = 7, a 1 = a +2 = 6 a +1 9 a, a 0 = 8, a 1 = a +2 = 6 a a, a 0 = 3, a 1 = 9 2i. 17. a +2 = a a, a 0 = 4, a 1 = a +2 = 14 a a, a 0 = 5, a 1 = a +2 = 8 a a, a 0 = 2, a 1 = a +2 = 7 a a, a 0 = 5, a 1 = a +2 = 2 a +1 + a, a 0 = 2, a 1 =

24 1 22. a +2 = a +1 a, a 0 = 4, a 1 = a +2 = 4 a +1 a, a 0 = 12, a 1 = a +2 = a a, a 0 = 2, a 1 = a +2 = 2 a a, a 0 = 8, a 1 = a +2 = 6 a +1 9 a, a 0 = 12, a 1 = a +2 = 4 a +1 5 a, a 0 = 5, a 1 = 10 i a +2 = 3 a +1 a, a 0 = 8, a 1 = a +2 = 14 a a, a 0 = 5, a 1 = a +2 = 4 a a, a 0 = 2, a 1 = a +2 = 4 a +1 5 a, a 0 = 3, a 1 = 6 7i. 32. a +2 = a a, a 0 = 5, a 1 = a +2 = 16 a a, a 0 = 7, a 1 = a +2 = 5 a +1 6 a, a 0 = 2, a 1 = a +2 = 10 a a, a 0 = 2, a 1 = 10 4i a +2 = 6 a +1 5 a, a 0 = 11, a 1 = a +2 = 2 a a, a 0 = 11, a 1 = a +2 = 6 a a ; a 0 = 3, a 1 = 0. Линейные однородные рекуррентные соотношения третьего порядка 39. a +3 = 7 a a a, a 0 = 1, a 1 = 3, a 2 = a +3 = 4 a +2 a +1 6 a, a 0 = 4, a 1 = 5, a 2 = a +3 = 6 a a a, a 0 = 5, a 1 = 8, a 2 = a +3 = 8 a a a, a 0 = 4, a 1 = 31, a 2 = a +3 = 5 a +2 3 a +1 9 a, a 0 = 1, a 1 = 3, a 2 = a +3 = 15 a a a, a 0 = 8, a 1 = 40, a 2 =

25 45. a +3 = 27 a a, a 0 = 6, a 1 = 3, a 2 = a +3 = 6 a a a, a 0 = 15, a 1 = 32, a 2 = a +3 = 15 a a a, a 0 = 1, a 1 = 20, a 2 = a +3 = 9 a a a, a 0 = 0, a 1 = 4, a 2 = a +3 = 2 a a +1 6 a, a 0 = 4, a 1 = 5, a 2 = a +3 = 4 a +2 5 a a, a 0 = 2, a 1 = 6, a 2 = a +3 = 6 a +2 5 a a, a 0 = 4, a 1 = 2, a 2 = a +3 = 3 a a a, a 0 = 2, a 1 = 17, a 2 = a +3 = 9 a a a, a 0 = 1, a 1 = 3, a 2 = a +3 = 6 a a +1 6 a, a 0 = 13, a 1 = 31, a 2 = a +3 = 5 a +2 3 a +1 9 a, a 0 = 3, a 1 = 14, a 2 = a +3 = a a +1 4 a, a 0 = 2, a 1 = 1, a 2 = a +3 = 3 a a a, a 0 = 2, a 1 = 3, a 2 = a +3 = 12 a a a, a 0 = 2, a 1 = 16, a 2 = a +3 = 4 a a a, a 0 = 0,2, a 1 = 6, a 2 = a +3 = 8 a a a, a 0 = 3, a 1 = 13, a 2 = a +3 = 4 a a a, a 0 = 3, a 1 = 29, a 2 = a +3 = 5 a +2 7 a a, a 0 = 11, a 1 = 34, a 2 = a +3 = 11 a a a, a 0 = 27, a 1 = 17, a 2 = a +3 = 12 a a a, a 0 = 1, a 1 = 37, a 2 = a +3 = 3 a a a, a 0 = 11, a 1 = 23, a 2 = a +3 = 7 a a a, a 0 = 3, a 1 = 6, a 2 = a +3 = 4 a a a, a 0 = 4, a 1 = 1, a 2 = 4.; 68. a +3 = 7 a a a, a 0 = 1, a 1 = 0, a 2 = a +3 = 5 a a a, a 0 = 6, a 1 = 0, a 2 = a +3 = 5 a +2 3 a a, a 0 = 10, a 1 = 1, a 2 = a +3 = 3 a +2 3 a +1 + a, a 0 = 2, a 1 = 4, a 2 = a +3 = 3 a a a, a 0 = 6, a 1 = 5, a 2 =

26 73. a +3 = 10 a a a, a 0 = 0, a 1 = 1, a 2 = a +3 = 8 a a a, a 0 = 8, a 1 = 23, a 2 = a +3 = 5 a +2 8 a +1 4 a, a 0 = 11, a 1 = 15, a 2 = a +3 = a a a, a 0 = 6, a 1 = 5, a 2 = a +3 = 10 a a a, a 0 = 1, a 1 = 2, a 2 = a +3 = a a a, a 0 = 1, a 1 = 14, a 2 = a +3 = 2 a +2 + a a, a 0 = 10, a 1 = 1, a 2 = a +3 = 5 a +2 8 a a, a 0 = 9, a 1 = 9, a 2 = a +3 = 8i a a +1 10i a, a 0 = 8, a 1 = 14i, a 2 = 38. Линейные рекуррентные соотношения первого порядка 82. a +1 = 4 a + 6, a 0 = a +1 = a + + 1, a 0 = a +1 = 5 a , a 0 = a +1 = 3 a + 5 2, a 0 = a +1 = 3 a + (4) 5 1, a 0 = a +1 = 4 a + 8 4, a 0 = a +1 = 3 a , a 0 = 14. Линейные рекуррентные соотношения второго порядка 89. a +2 = 7 a a + 10, a 0 = 4, a 1 = a +2 = 10 a a + 32, a 0 = 1, a 1 = a +2 = 6 a +1 9 a 2 3, a 0 = 0, a 1 = a +2 = 7 a a , a 0 = 3, a 1 = a +2 = 9 a a + (18 20) 2, a 0 = 6, a 1 = a +2 = 8 a +1 7 a , a 0 = 9, a 1 = a +2 = 4 a +1 9 a , a 0 = 15, a 1 = 27 i a +2 = 12 a a , a 0 = 13, a 1 = 6. 26

Благовещенский государственный педагогический университет кафедра алгебры, геометрии и МПМ 16 апреля 2011 г. 1 Решение рекуррентных соотношений Определение Рекуррентным соотношением называется соотношение

Лекция 3. Последовательности, определяемые рекуррентными соотношениями. Однородные и неоднородные линейные рекуррентные уравнения (ЛОРУ и ЛНРУ). Общие решения ЛОРУ и ЛНРУ. Лектор - доцент Селезнева Светлана

Лекция: Последовательности. Однородные и неоднородные линейные рекуррентные уравнения. Общие решения линейных рекуррентных однородных и неоднородных уравнений. Лектор - доцент Селезнева Светлана Николаевна

Лекция. Функции натурального аргумента (последовательности). Однородные и неоднородные линейные рекуррентные уравнения (ЛОРУ и ЛНРУ). Общие решения ЛОРУ и ЛНРУ. Примеры Лектор - доцент Селезнева Светлана

РЕШЕНИЕ РЕКУРРЕНТНЫХ УРАВНЕНИЙ Обозначим через значение некоторого выражения при подстановке в него целого числа Тогда зависимость члена последовательности от членов последовательности F F со значениями

Пензенский государственный педагогический университет им В Г Белинского О А Монахова, Н А Осьминина Рекуррентные последовательности Алгебра формальных рядов Методические рекомендации для студентов специальностей

Лекция 3. Последовательности, определяемые рекуррентными соотношениями. Однородные и неоднородные линейные рекуррентные уравнения (ЛОРУ и ЛНРУ). Общие решения ЛОРУ и ЛНРУ. Примеры Лектор - доцент Селезнева

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»

Министерство транспорта Российской Федерации ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)» Кафедра «Математический анализ»

Лекции по Математике Вып ТММ- Ю В Чебраков ТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ Санкт-Петербург, 00 УДК 5+5 ББК Ч35 Р е ц е н з е н т ы: Доктор физико-математических наук, профессор С-Петерб техн ун-та М А Салль Кандидат

А А КИРСАНОВ КОМПЛЕКСНЫЕ ЧИСЛА ПСКОВ ББК 57 К45 Печатается по решению кафедры алгебры и геометрии, и редакционно-издательского совета ПГПИ им СМ Кирова Рецензент: Медведева ИН, кандидат физ мат наук, доцент

Михайлова Инна Анатольевна Институт математики и естественных наук. Кафедра алгебры и фундаментальной информатики. 30 сентября 2018 г. Примеры Числа Фибоначчи Числа Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21,...

Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Понятие многочлена Определения Многочленом от одной переменной называется выражение вида

Глава 0 ПОСЛЕДОВАТЕЛЬНОСТИ Алгоритмы А- Задание числовых последовательностей А- Арифметическая прогрессия А- Геометрическая прогрессия А- Суммирование А-5 Бесконечно убывающая геометрическая прогрессия

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 0 класс МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ И БЕСКОНЕЧНЫЕ ЧИСЛОВЫЕ

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Ухтинский государственный технический университет (УГТУ) ПРЕДЕЛ ФУНКЦИИ Методические

ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ Геометрической прогрессией называется числовая последовательность b, первый член которой отличен от нуля, а каждый последующий член, начиная со второго,

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное общеобразовательное учреждение высшего профессионального образования «Тверской государственный университет» Математический факультет Кафедра алгебры

Глава 0 ТЕСТОВЫЕ ЗАДАНИЯ И ДИКТАНТЫ Т-00 Вычисление членов последовательности по рекуррентной формуле Т-00 Составление рекуррентной формулы Т-00 Формула общего члена Т-004 Составление арифметической прогрессии

6-7 уч год 6, кл Математика Комплексные числа 4 Алгебраические уравнения Квадратные уравнения В школьном курсе алгебры рассматривались квадратные уравнения ax bx c =, a, () с действительными коэффициентами

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МАШИНОСТРОЕНИЯ ИИ Поспелов,

Лекция Глава Множества и операции над ними Понятие множества Понятие множество относится к наиболее первичным понятиям математики не определяемым через более простые Под множеством понимают совокупность

Лекции по Математике. Вып. ТММ-1 Ю. В. Чебраков ТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ Санкт-Петербург, 010 УДК 511+51 ББК Ч345 Р е ц е н з е н т ы: Доктор физико-математических наук, профессор С.-Петерб. техн. ун-та

Прогрессии Последовательность функция натурального аргумента.. Задание последовательности формулой общего члена: a n = f(n), n N, например, a n = n + n + 4, а = 43, а = 47, а 3 = 3,. Задание последовательности

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Общие понятия Дифференциальные уравнения имеют многочисленные и самые разнообразные приложения в механике физике астрономии технике и в других разделах высшей математики (например

Оглавление Введение. Основные понятия.... 4 1. Интегральные уравнения Вольтерры... 5 Варианты домашних заданий.... 8 2. Резольвента интегрального уравнения Вольтерры. 10 Варианты домашних заданий.... 11

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. Н. И. ЛОБАЧЕВСКОГО Факультет вычислительной математики и кибернетики Кафедра математической

Лекция. Задача о кроликах. Числа Фибоначчи, последовательность Фибоначчи, рекуррентная формула 3. Свойства чисел Фибоначчи (a) Линейность (b) Теоретико-числовые свойства (c) Суммы: F + F +... + F n, нечетных

ЛИНЕЙНАЯ АЛГЕБРА Издательство ТГТУ Министерство образования и науки Российской Федерации ГОУ ВПО "Тамбовский государственный технический университет" ЛИНЕЙНАЯ АЛГЕБРА Методические указания для студентов

Тишин В И Основные методы решения тригонометрических уравнений г Тишин В И Математика для учителей и учащихся Материал подготовлен учителем математики Тишиным Владимиром Ивановичем года Тишин В И Основные

Дифференциальные уравнения высшего порядка. Конев В.В. Наброски лекций. Содержание 1. Основные понятия 1 2. Уравнения, допускающие понижение порядка 2 3. Линейные дифференциальные уравнения высшего порядка

Лекция.7. Расширение понятия числа. Комплексные числа, действия над ними Аннотация: В лекции указывается на необходимость обобщения понятия числа от натурального до комплексного. Вводятся алгебраическая,

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Лекция 3 Ряды Тейлора и Маклорена Применение степенных рядов Разложение функций в степенные ряды Ряды Тейлора и Маклорена Для приложений важно уметь данную функцию разлагать в степенной ряд, те функцию

Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Вступительные замечания В этой лекции мы приступаем к изучению линейной алгебры как таковой,

Тема 2-11: Собственные векторы и собственные значения А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Заочная школа Математическое отделение МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ И БЕСКОНЕЧНЫЕ ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ 0-й класс, задание ПРАВИЛА ОФОРМЛЕНИЯ ЗАДАНИЯ Приступая

ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ По дисциплине: «Алгебра» Специальность: «Математика» заочная форма обучения 6 семестр Составитель: зав кафедрой Трофимук АА Многочлены от нескольких переменных результант алгебраические

Указания, решения, ответы УРАВНЕНИЯ В ЦЕЛЫХ ЧИСЛАХ. Уравнение с одной неизвестной.. Решение. Подставим в уравнение. Получим равенство (4a b 4) (a b 8) 0. Равенство A B 0, где А и В целые, выполняется,

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ Лекция. Понятие множества. Определение функции основные свойства. Основные элементарные функции СОДЕРЖАНИЕ: Элементы теории множеств Множество вещественных чисел Числовая

Рабочая программа по алгебре для учащихся 8-9 классов разработана на основе требований к результатам освоения основной образовательной программы основного общего образования. Рабочая программа рассчитана

Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Вступительные замечания При решении многих задач возникает необходимость иметь числовые

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕР- ВОГО ПОРЯДКА.. Основные понятия Дифференциальным уравнением называется уравнение, в которое неизвестная функция входит под знаком производной или дифференциала.

СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ Приведение к одному уравнению -го порядка С практической точки зрения очень важны линейные системы с постоянными коэффициентами

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Нижегородский государственный университет им НИ Лобачевского Национальный исследовательский университет АВ Леонтьева СБОРНИК ЗАДАЧ (МЕТОД МАТЕМАТИЧЕСКОЙ

АГЕНТСТВО ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ КРАСНОЯРСКОГО КРАЯ КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЗАОЧНАЯ ЕСТЕСТВЕННО-НАУЧНАЯ ШКОЛА при КрасГУ ДОПОЛНИТЕЛЬНЫЕ ГЛАВЫ МАТЕМАТИКИ 10 класс Модуль 4 МЕТОДЫ РЕШЕНИЯ

Министерство образования Российской Федерации Российский государственный университет нефти и газа имени ИМ Губкина ВИ Иванов Методические указания к изучению темы «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ» (для студентов

СТЕПЕНЬ С ДРОБНЫМ ПОКАЗАТЕЛЕМ Если показатель t степени числа является дробным, те t, N, то для неотрицательных значений (0) по определению полагают def Для отрицательных чисел (0) < операция возведения

Министерство сельского хозяйства Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермская государственная сельскохозяйственная академия имени

РАЦИОНАЛЬНЫЕ ЧИСЛА Обыкновенные дроби Определение Дроби вида, называются обыкновенными дробями Обыкновенные дроби, правильные и неправильные Определение Дробь, правильной, если < при, где Z, N Z, N Z,

Лекция. 5. ОПИСАНИЕ И АНАЛИЗ ДИСКРЕТНЫХ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ РАЗНОСТНЫХ УРАВНЕНИЙ 5.. ОДНОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ ВОЗДЕЙСТВИЯХ 5... Описание сигналов и систем. Описание сигналов. Сигналы

В заключение этого пункта заметим что говорят также о собственных векторах матрицы порядка имея при этом ввиду собственные векторы оператора -мерного пространства имеющего своей матрицей в некотором базисе

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ Интегрирование рациональных дробей Рациональной дробью называется дробь вида P Q, где P и Q многочлены Рациональная дробь называется правильной, если степень многочлена P ниже степени

Тема 14 «Алгебраические уравнения и системы нелинейных уравнений» Многочленом степени n называется многочлен вида P n () a 0 n + a 1 n-1 + + a n-1 + a n, где a 0, a 1, a n-1, a n заданные числа, a 0,

Тема: Общая теория систем линейных уравнений А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Московский государственный университет геодезии и картографии (МИИГАиК) Факультет дистанционных форм обучения Заочное отделение `` МЕТОДИЧЕСКИЕ УКАЗАНИЯ,

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОМЫШЛЕННЫХ

Решить дифференциальное уравнение Решение: составим и решим характеристическое уравнение:, Получены два различных действительных корня Всё, что осталось сделать записать ответ, руководствуясь формулой

ЛЕКЦИЯ КОМПЛЕКСНЫЕ ЧИСЛА РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ Числовые множества Множество комплексных чисел Многочлены с вещественными коэффициентами Разложение на множители ЧИСЛОВЫЕ МНОЖЕСТВА МНОЖЕСТВО

РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ

РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ

(от лат. recur-rens, род. падеж recurrentis - возвращающийся) - однотипные ф-лы, к-рые связывают между собой идущие друг за другом нек-рой последовательности (это может быть последовательность чисел, ф-ций и т. д.). В зависимости от природы объектов, связанных Р. с., эти соотношения могут быть алгебраическими, функциональными, дифференциальными, интегральными и т. п.

Наиб. известный класс Р. с.- это рекуррентные ф-лы для специальных функций. Так, для цилиндрических функций Z m (x )P. с. имеют вид

Они позволяют по ф-ции Z m0 (x )найти ф-ции Z m (x )п-ри т = т 0 b 1, т 0 b 2 и т. д. либо, напр., по значениям ф-ций в нек-рой точке х 0 . 0 найти (в численных расчётах) значение любой из ф-ций

В этой же точке (здесь m 0 - любое вещественное число).

Др. важный класс Р. с. дают многочисленные методы последовательных приближений (см. Итераций метод); сюда же примыкают и методы возмущений теории.

В квантовой механике есть ещё один вид Р. с., связывающих между собой векторы в гильбертовом пространстве состояний. Напр., стационарные гармония, осциллятора параметризуются целыми неотрицательными числами. Соответствующие векторы, обозначаемые , где n - целое, при разных n могут быть получены друг из друга действием операторов рождения а + и уничтожения а :

Эти соотношения можно разрешить, выразив любой вектор через (наинизшее энергетич. состояние, h = 0):

Обобщением этой конструкции является представление вторичного квантования в квантовой статистич. механике и квантовой теории поля (см. Фока пространство).

Типичный пример Р. с. в статистич. механике - ур-ния для частичных ф-ций распределения, образующие цепочку Боголюбова (см. Боголюбова уравнения); знание таких ф-ций позволяет найти все термодинамич. характеристики системы.

В квантовой теории поля динамич. содержится, напр., в Грина функциях. Для их вычисления используют разл. приближения, чаще всего - расчеты по теории возмущений. Альтернативный подход основан на интегродифференциальных Дайсона уравнениях, являющихся Р. с.: ур-ние для двухточечной ф-ции Грина содержит четырёхточечную и т. д. Как и ур-ния Боголюбова, эту систему удаётся решать, лишь "оборвав" цепочку (место "обрыва" выбирается обычно из физ. соображений и определяет получаемое ).

Ещё один вид Р. с. в квантовой теории поля - У орда тождества в теориях калибровочных полей. Эти тождества также представляют собой цепочку интегродифференциальных соотношений, связывающих между собой ф-ции Грина с разл. числом внешних линий, p являются следствием калибровочной инвариантности теории. Решающую роль они играют для проверки калибровочной симметрии при проведении процедуры перенормировки.

Наконец, сама - тоже рекуррентная процедура: на каждом шаге (в каждой следующей петле) используются контрчлены, полученные из вычисления диаграмм с меньшим числом петель (подробнее см. R-операция). А. М. Малокостов.

Физическая энциклопедия. В 5-ти томах. - М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Смотреть что такое "РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ" в других словарях:

рекуррентные соотношения - — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN recurrence relations … Справочник технического переводчика

- (функции Вебера) общее название для специальных функций, являющихся решениями дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнений математической физики, таких как уравнение Лапласа, уравнение… … Википедия

Или считалка Джозефуса известная математическая задача с историческим подтекстом. Задача основана на легенде, что отряд Иосифа Флавия, защищавший город Йодфат, не пожелал сдаваться в плен блокировавшим пещеру превосходящими силам римлян.… … Википедия

Пафнутий Львович Чебышёв В математике последовательностью ортогональных многочленов называют бесконечную последовательность действительных многочленов … Википедия

Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия

Последовательность Падована это целочисленная последовательность P(n) с начальными значениями и линейным рекуррентным соотношением Первые значения P(n) таковы 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 … Википедия

Многочлены Эрмита определённого вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1… … Википедия

- (функции Бесселя) решения Zv(z)ур ния Бесселя где параметр (индекс) v произвольное действительное или комплексное число. В приложениях чаще встречается ур ние, зависящее от четырёх параметров: решения к рого выражаются через Ц … Физическая энциклопедия

Метод решения системы линейных алгебраич. уравнений А х= b с эрмитовой невырожденной матрицей А. Среди прямых методов он наиболее эффективен при реализации на ЭВМ. Вычислительная схема метода в общем случае основана на факторизации эрмитовой… … Математическая энциклопедия

Модифицированные функции Бесселя это функции Бесселя от чисто мнимого аргумента. Если в дифференциальном уравненни Бесселя заменить на, оно примет вид Это уравнение называется модифицированным уравнением Бессел … Википедия