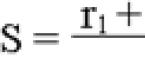Многогранник

• Многогранник - это такое тело, поверхность которого состоит из конечного числа плоских многоугольников.

Многогранник называется выпуклым

• Многогранник называется выпуклым ,если он расположен по одну сторону каждого плоского многоугольника на его поверхности.

• Евклид (предположительно 330- 277 до н.э.) – математик Александрийской школы Древней Греции,автор первого дошедшего до нас трактата по математике «Начала» (в 15 книгах)

боковыми гранями .

• Призма-многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники Ф и Ф1, лежащие в параллельных плоскостях, называют основаниями призмы, а остальные грани - боковыми гранями .

• Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания.

• Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют прямой ; если боковое ребро призмы не перпендикулярно плоскости ее основания, то такую призму называют наклонной . У прямой призмы боковые грани - прямоугольники.

Основания призмы равны.

• Основания призмы равны.

• У призмы основания лежат в параллельных плоскостях.

• У призмы боковые ребра параллельны и равны.

• Высотой призмы называется расстояние между плоскостями ее оснований.

• Оказывается,что призма может быть не только геометрическим телом,но и художественным шедевром.Именно призма стала основой картин Пикассо,Брака,Грисса и т.д.

• Оказывается,что снежинка может принять форму шестигранной призмы,но это будет зависеть от температуры воздуха.

• В III веке до н. э. был построен маяк, чтобы корабли могли благополучно миновать рифы на пути в александрийскую бухту. Ночью им помогало в этом отражение языков пламени, а днём- столб дыма. Это был первый в мире маяк, и простоял он 1500 лет.

• Маяк был построен на маленьком острове Фарос в Средиземном море, около берегов Александрии. На его строительство ушло 20 лет, а завершён он был около 280 года до н.э.

• В XIV веке маяк был уничтожен землетрясением. Его обломки использовали при строительстве военного форта. Форт не раз перестраивался и до сих пор стоит на месте первого в мире маяка.

Мавсол был правителем Карий. Столицей области был Галикарнас. Мавсол женился на своей сестре Артемизии. Он решил построить гробницу для себя и своей царицы. Мавсол мечтал о величественном памятнике, который бы напоминал миру о его богатстве и могуществе. Он умер до окончания работ над гробницей. Руководить строительством продолжила Артемизия. Гробница была построена в 350 году до н. э. Она была названа Мавзолеем по имени царя.

Пепел царственной четы хранился в золотых урнах в усыпальнице в основании здания. Ряд каменных львов сторожил это помещение. Само сооружение напоминало греческий храм, окружённый колоннами и статуями. На вершине здания находилась ступенчатая пирамида. На высоте 43 м над землёй её венчало скульптурное изображение колесницы, запряжённой лошадьми. На ней, вероятно, стояли статуи царя и царицы.

• Спустя восемнадцать столетий землетрясение разрушило Мавзолей до основания. Ещё триста лет прошло, прежде чем археологи приступили к раскопкам. В 1857 году все находки были перевезены в Британский музей в Лондоне. Теперь на месте, где когда-то был Мавзолей, осталась лишь горстка камней.

кристаллы .

Существуют не только геометрические формы,созданные руками человека.Их много и в самой природе.Воздействие на облик земной поверхности таких природных факторов,как ветер,вода,солнечный свет,весьма стихийно и носит беспорядочный характер.Однако песчаные дюны,галька на морском берегу,кратер потухшего вулкана имеют,как правило,геометрически правильные формы.В земле иногда находят камни такой формы,как будто их кто-то тщательно выпиливал,шлифовал,полировал.Это - кристаллы .

параллелепипедом .

• Если основание призмы есть параллелограмм,то он называется параллелепипедом .

• Моделями прямоугольного параллелепипеда служат:

• классная комната

• Оказывается,что кристаллы кальцита,сколько их не дроби на более мелкие части,всегда распадаются на осколки,имеющие форму параллелепипеда.

• Городские здания чаще всего имеют форму многогранников.Как правило,это обычные параллелепипеды.И лишь неожиданные архитектурные решения украшают города.

• 1.Является ли призма правильной, если её ребра равны?

• а)да; в) нет. Обоснуйте свой ответ.

• 2.Высота правильной треугольной призмы равна 6 см. Сторона основания равна 4 см. Найдите площадь полной поверхности этой призмы.

• 3. Площади двух боковых граней наклонной треугольной призмы равны 40 и 30 см2. Угол между этими гранями прямой. Найдите площадь боковой поверхности призмы.

• 4. В параллелепипеде ABCDA1B1C1D1 проведены сечения A1BC и CB1D1. В каком отношении эти плоскости делят диагональ AC1.

• 1) тетраэдр, имеющий 4 грани, 4 вершины, 6 ребер;

• 2) куб - 6 граней, 8 вершин, 12 ребер;

• 3) октаэдр - 8 граней, 6 вершин, 12 ребер;

• 4) додекаэдр - 12 граней, 20 вершин, 30 ребер;

• 5) икосаэдр - 20 граней, 12 вершин, 30 ребер.

Фалеса Милетского , основателя ионийской Пифагора Самосского

Ученые и философы Древней Греции восприняли и переработали достижения культуры и науки Древнего Востока. Фалес, Пифагор, Демокрит, Евдокс и др. ездили в Египет и Вавилон для изучения музыки, математики и астрономии. Не случайно зачатки греческой геометрической науки связаны с именем Фалеса Милетского , основателя ионийской школы. Ионийцы, населявшие территорию, которая граничила с восточными странами, первыми заимствовали знания Востока и стали их развивать. Ученые ионийской школы впервые подвергли логической обработке и систематизировали математические сведения, позаимствованные у древневосточных народов, в особенности у вавилонян. Фалесу, главе этой школы, Прокл и другие историки приписывают немало геометрических открытий. Об отношении Пифагора Самосского к геометрии Прокл пишет в своем комментарии к "Началам" Евклида следующее: "Он изучал эту науку (т. е. геометрию), исходя от первых ее оснований, и старался получать теоремы при помощи чисто логического мышления". Прокл приписывает Пифагору, кроме известной теоремы о квадрате гипотенузы, еще построение пяти правильных многогранников:

Тела Платона

Тела Платона -это выпуклые многогранники, все грани которых правильные многоугольники. Все многогранные углы правильного многогранника конгруэнтны. Как это следует уже из подсчета суммы плоских углов при вершине, выпуклых правильных многогранников не больше пяти. Указанным ниже путем можно доказать, что существует именно пять правильных многогранников (это доказал Евклид). Они - правильный тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.

Октаэдр (рис.3).

• Октаэдр -восьмигранник; тело, ограниченное восемью треугольниками; правильный октаэдр ограничен восемью равносторонними треугольниками; один из пяти правильных многогранников. (рис.3).

• Додекаэдр -двенадцатигранник, тело, ограниченное двенадцатью многоугольниками; правильный пятиугольник; один из пяти правильных многогранников. (рис.4).

• Икосаэдр -двадцатигранник, тело, ограниченное двадцатью многоугольниками; правильный икосаэдр ограничен двадцатью равносторонними треугольниками; один из пяти правильных многогранников. (рис.5).

Грани додекаэдра являются правильными пятиугольниками. Диагонали же правильного пятиугольника образуют так называемый звездчатый пятиугольник - фигуру, которая служила эмблемой, опознавательным знаком для учеников Пифагора. Известно, что пифагорейский союз был одновременно философской школой, политической партией и религиозным братством. Согласно легенде, один пифагореец заболел на чужбине и не мог перед смертью расплатиться с ухаживавшим за ним хозяином дома. Последний нарисовал на стене своего дома звездчатый пятиугольник. Увидав через несколько лет этот знак, другой странствующий пифагореец осведомился о случившемся у хозяина и щедро его вознаградил.

• Достоверных сведений о жизни и научной деятельности Пифагора не сохранилось. Ему приписывается создание учения о подобии фигур. Он, вероятно, был среди первых ученых, рассматривавших геометрию не как практическую и прикладную дисциплину, а как абстрактную логическую науку.

В школе Пифагора было открыто существование несоизмеримых величин, т. е. таких, отношение между которыми невозможно выразить никаким целым или дробным числом. Примером может служить отношение длины диагонали квадрата к длине его стороны, равное Ц2. Число это не является рациональным (т. е. целым или отношением двух целых чисел) и называется иррациональным, т.е. нерациональным (от латинского ratio - отношение).

Тетраэдр (рис.1).

• Тетраэдр -четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти правильных многоугольников. (рис.1).

• Куб или правильный гексаэдр (рис.2).

Тетраэдр -четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти правильных многоугольников. (рис.1).

• Тетраэдр -четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти правильных многоугольников. (рис.1).

• Куб или правильный гексаэдр - правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами. (рис.2).

Пирамида

• Пирамида -многогранник, который состоит из плоского многоугольника- основание пирамиды, точки, не лежащие в плоскости основания-вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания

На рисунке изображены пятиугольная пирамида SABCDE и ее развертка. Треугольники, имеющие общую вершину, называют боковыми гранями пирамиды; общую вершину боковых граней - вершиной пирамиды; многоугольник, которому не принадлежит эта вершина,- основанием пирамиды; ребра пирамиды, сходящиеся в ее вершине,- боковыми ребрами пирамиды. Высота пирамиды - это отрезок перпендикуляра, проведенного через ее вершину к плоскости основания, с концами в вершине и на плоскости основания пирамиды. На рисунке отрезок SO - высота пирамиды.

• Определение . Пирамида, основание которой - правильный многоугольник и вершина проектируется в его центр, называется правильной.

• На рисунке изображена правильная шестиугольная пирамида.

Объемы зерновых амбаров и других сооружений в виде кубов, призм и цилиндров египтяне и вавилоняне, китайцы и индийцы вычисляли путем умножения площади основания на высоту. Однако древнему Востоку были известны в основном только отдельные правила, найденные опытным путем, которыми пользовались для нахождения объемов для площадей фигур. В более позднее время, когда геометрия сформировалась как наука, был найден общий подход к вычислению объемов многогранников.

• Среди замечательных греческих ученых V - IV вв. до н.э., которые разрабатывали теорию объемов, были Демокрит из Абдеры и Евдокс Книдский.

• Евклид не применяет термина "объем". Для него термин "куб", например, означает и объем куба. В ХI книге "Начал" изложены среди других и теоремы следующего содержания.

• 1. Параллелепипеды с одинаковыми высотами и равновеликими основаниями равновелики .

• 2. Отношение объемов двух параллелепипедов с равными высотами равно отношению площадей их оснований .

• 3. В равновеликих параллелепипедах площади оснований обратно пропорциональны высотам .

• Теоремы Евклида относятся только к сравнению объемов, так как непосредственное вычисление объемов тел Евклид, вероятно, считал делом практических руководств по геометрии. В произведениях прикладного характера Герона Александрийского имеются правила для вычислений объема куба, призмы, параллелепипеда и других пространственных фигур.

• Призма, основание которой - параллелограмм, называется параллелепипедом.

• В соответствии с определением параллелепипед - это четырехугольная призма, все грани которой - параллелограммы . Параллелепипеды, как и призмы, могут быть прямыми и наклонными . На рисунке 1 изображен наклонный параллелепипед, а на рисунке 2- прямой параллелепипед.

• Прямой параллелепипед, основанием которого служит прямоугольник, называют прямоугольным параллелепипедом . У прямоугольного параллелепипеда все грани - прямоугольники. Моделями прямоугольного параллелепипеда служат классная комната, кирпич, спичечная коробка.

• Длины трех ребер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями . Например, имеются спичечные коробки с измерениями 15, 35, 50 мм. Куб - прямоугольный параллелепипед с равными измерениями. Все шесть граней куба - равные квадраты.

• Рассмотрим некоторые свойства параллелепипеда.

• Теорема. Параллелепипед симметричен относительно середины его диагонали.

• Из теоремы непосредственно следуют важные свойства параллелепипеда :

• 1. Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам. 2. Противолежащие грани параллелепипеда параллельны и равны

Введение

Поверхность, составленную из многоугольников и ограничивающую некоторые геометрическое тело, называют многогранной поверхностью или многогранником.

Многогранником называется ограниченное тело, поверхность которого состоит из конечного числа многоугольников. Многоугольники, которые ограничивают многогранник, называются гранями, линии пересечения граней называются ребрами.

Многогранники могут иметь разнообразное и очень сложное строение. Различные постройки, например строящиеся дома из кирпичей и бетонных блоков, представляют собой примеры многогранников. Другие примеры можно найти среди мебели, например стол. В химии форма молекул углеводорода представляет собой тетраэдр, правильного двадцатигранника, куб. В физики примером многогранников служат кристаллы.

С древнейших времен представления о красоте связывали с симметрией. Наверное, этим объясняется интерес человека к многогранникам - удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей, которых поражала красота, совершенство, гармония этих фигур.

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.

Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики - это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.

Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел:

§ Вселенная - додекаэдр

§ Земля - куб

§ Огонь - тетраэдр

§ Вода - икосаэдр

§ Воздух - октаэдр

Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ - идеалист Платон. С тех пор правильные многогранники стали называться Платоновыми телами.

Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и углы которых равны, причем грани - правильные многоугольники. К каждой вершине правильного многогранника сходится одно и то же число рёбер. Все двугранные углы при рёбрах и все многогранные углы при вершинах правильного многоугольника равны. Платоновы тела - трехмерный аналог плоских правильных многоугольников.

Теория многогранников является современным разделом математики. Она тесно связана с топологией, теорией графов, имеет большое значение как для теоретических исследований по геометрии, так и для практических приложений в других разделах математики, например, в алгебре, теории чисел, прикладной математики - линейном программировании, теории оптимального управления. Таким образом, данная тема является актуальной, а знания по данной проблематике – важными для современного общества.

Основная часть

Многогранникомназывается ограниченное тело, поверхность которого состоит из конечного числа многоугольников.

Приведем определение многогранника, равносильное первому определению многогранника.

Многогранник– это фигура, являющаяся объединением конечного числа тетраэдров, для которых выполнены следующие условия:

1) каждые два тетраэдра не имеют общих точек, либо имеют общую вершину, либо только общее ребро, либо целую общую грань;

2) от каждого тетраэдра к другому можно перейти по цепочке тетраэдра, в которой каждый последующий прилегает к предыдущему по целой грани.

Элементы многогранника

Грань многогранника – это некоторый многоугольник (многоугольником называется ограниченная замкнутая область, граница которой состоит из конечного числа отрезков).

Стороны граней называются ребрами многогранника, а вершины граней – вершинамимногогранника. К элементам многогранника, кроме его вершин, ребер и граней, относятся также плоские углы его граней и двугранные углы при его ребрах. Двугранный угол при ребре многогранника определяется его гранями, подходящими к этому ребру.

Классификация многогранников

Выпуклый многогранник - это многогранник, любые две точки которого соединимы в нем отрезком. Выпуклые многогранники обладают многими замечательными свойствами.

Теорема Эйлера. Для любого выпуклого многогранника В-Р+Г=2,

Где В – число его вершин, Р - число его ребер, Г - число его граней.

Теорема Коши. Два замкнутых выпуклых многогранника, одинаково составленные из соответственно равных граней равны.

Выпуклый многогранник считается правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходиться одно и то же число ребер.

Правильный многогранник

Многогранник называется правильным, если, во-первых, он выпуклый, во-вторых, все его грани - равные друг другу правильные многоугольники, в-третьих, в каждой его вершине сходятся одинаковое число граней, и, в-четвертых, все его двугранные углы равны.

Существует пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида (древнегреческий математик, автор первых дошедших до нас теоретических трактатов по математике). Почему правильные многогранники получили такие имена? Это связано с числом их граней. Тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" - грань. Гексаэдр (куб) имеет 6 граней, "гекса" - шесть; октаэдр - восьмигранник, "окто" - восемь; додекаэдр - двенадцатигранник, "додека" - двенадцать; икосаэдр имеет 20 граней, "икоси" - двадцать.

2.3. Типы правильных многогранников:

1) Правильный тетраэдр (составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольник. Следовательно, сумма плоских углов при каждой вершине равна 180 0);

2) Куб - параллелепипед, все грани которого – квадраты. Куб составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270 0 .

3) Правильный октаэдр или просто октаэдр – многогранник, у которого восемь правильных треугольных граней и в каждой вершине сходятся по четыре грани. Октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240 0 . Его можно построить, сложив основаниями две пирамиды, в основании которых квадраты, а боковые грани - правильные треугольники. Ребра октаэдра можно получить, соединяя центры соседних граней куба, если же соединить центры соседних граней правильного октаэдра, то получим ребра куба. Говорят, что куб и октаэдр двойственны друг другу.

4)Икосаэдр - составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300 0 .

5) Додекаэдр - многогранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324 0 .

Додекаэдр и икосаэдр тоже двойственны друг другу в том смысле, что, соединив отрезками центры соседних граней икосаэдра, мы получим додекаэдр, и наоборот.

Правильный тетраэдр двойственен сам себе.

При этом не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники при n ≥ 6.

Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны. Но есть и такие многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные правильные многоугольники. Многогранники такого типа называются равноугольно-полуправильными многогранниками. Впервые многогранники такое типа открыл Архимед. Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда. Это усеченный тетраэдр, усеченный оксаэдр, усеченный икосаэдр, усеченный куб, усеченный додекаэдр, кубооктаэдр, икосододекаэдр, усеченный кубооктаэдр усеченный икосододекаэдр, ромбокубооктаэдр, ромбоикосододекаэдр, "плосконосый" (курносый) куб, "плосконосый" (курносый) додекаэдр.

2.4. Полуправильные многогранники или Архимедовы тела - выпуклые многогранники, обладающие двумя свойствами:

1. Все грани являются правильными многоугольниками двух или более типов (если все грани - правильные многоугольники одного типа, это - правильный многогранник).

2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую. В частности все многогранные углы при вершинах конгруэнтны.

Кроме полуправильных многогранников из правильных многогранников - Платоновых тел, можно получить так называемые правильные звездчатые многогранники. Их всего четыре, они называются также телами Кеплера-Пуансо. Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.

Два тетраэдра, прошедших один сквозь другой, образуют восьмигранник. Иоганн Кеплерприсвоил этой фигуре имя «стелла октангула» - «восьмиугольная звезда». Она встречается и в природе: это так называемый двойной кристалл.

В определении правильного многогранника сознательно - в расчете на кажущуюся очевидность - не было подчеркнуто слово «выпуклый». А оно означает дополнительное требование: «и все грани, которого лежат по одну сторону от плоскости, проходящей через любую из них». Если же отказаться от такого ограничения, то к Платоновым телам, кроме «продолженного октаэдра», придется добавить еще четыре многогранника (их называют телами Кеплера - Пуансо), каждый из которых будет «почти правильным». Все они получаются «озвездыванием» Платонова тела, то есть продлением его граней до пересечения друг с другом, и потому называются звездчатыми. Куб и тетраэдр не порождают новых фигур - грани их, сколько ни продолжай, не пересекаются.

Если же продлить все грани октаэдра до пересечения их друг с другом, то получится фигура, что возникает при взаимопроникновении двух тетраэдров - «стелла октангула», которая называется «продолженным октаэдром».

Икосаэдр и додекаэдр дарят миру сразу четыре «почти правильных многогранника». Один из них - малый звездчатый додекаэдр, полученный впервые Иоганном Кеплером.

Столетиями математики не признавали за всякого рода звездами права называться многоугольниками из-за того, что стороны их пересекаются. Людвиг Шлефли не изгонял геометрическое тело из семейства многогранников только за то, что его грани самопересекаются, тем не менее, оставался непреклонным, как только речь заходила про малый звездчатый додекаэдр. Довод его был прост и весом: это кеплеровское животное не подчиняется формуле Эйлера! Его колючки образованы двенадцатью гранями, тридцатью ребрами и двенадцатью вершинами, и, следовательно, В+Г-Р вовсе не равняется двойке.

Шлефли был и прав, и не прав. Конечно же, геометрический ежик не настолько уж колюч, чтобы восстать против непогрешимой формулы. Надо только не считать, что он образован двенадцатью пересекающимися звездчатыми гранями, а взглянуть на него как на простое, честное геометрическое тело, составленное из 60 треугольников, имеющее 90 ребер и 32 вершины.

Тогда В+Г-Р=32+60-90 равно, как и положено, 2. Но зато тогда к этому многограннику неприменимо слово «правильный» - ведь грани его теперь не равносторонние, а всего лишь равнобедренные треугольники. Кеплер не додумался, что у полученной им фигуры есть двойник.

Многогранник, который называется «большой додекаэдр» - построил французский геометр Луи Пуансо спустя двести лет после кеплеровских звездчатых фигур.

Большой икосаэдрбыл впервые описан Луи Пуансо в 1809 году. И опять Кеплер, увидев большой звездчатый додекаэдр, честь открытия второй фигуры оставил Луи Пуансо. Эти фигуры также наполовину подчиняются формуле Эйлера.

Практическое применение

Многогранники в природе

Правильные многогранники – самые выгодные фигуры, поэтому они широко распространены в природе. Подтверждением тому служит форма некоторых кристаллов. Например, кристаллы поваренной соли имеют форму куба. При производстве алюминия пользуются алюминиево-калиевыми кварцами, монокристалл которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана. Кристаллы этого химического вещества имеют форму додекаэдра. В разных химических реакциях применяется сурьменистый сернокислый натрий – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра. Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора.

Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.

Правильные многогранники встречаются так же и в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Оно больше похоже на звёздчатый многогранник.

Также мы можем наблюдать многогранники в виде цветов. Ярким примером могут служить кактусы.

Похожая информация.

Изучая многоугольники, говорят о плоском многоугольнике, понимая под ним сам многоугольник и его внутреннюю область.

То же самое происходит и в стереометрии. По аналогии с понятием плоского многоугольника вводится понятие тела и его поверхности.

Точка геометрической фигуры называется внутренней, если существует шар с центром в этой точке, целиком принадлежащий этой фигуре. Фигура называется областью, если все

ее точки внутренние и если любые две ее точки можно соединить ломаной, целиком принадлежащей фигуре.

Точка пространства называется граничной точкой данной фигуры, если любой шар с центром в этой точке содержит как точки, принадлежащие фигуре, так и точки, не принадлежащие ей. Граничные точки области образуют границу области.

Телом называется конечная область вместе с ее границей. Граница тела называется поверхностью тела. Тело называется простым, если его можно разбить на конечное число треугольных пирамид.

Телом вращения в простейшем случае называется такое тело, которое плоскостями, перпендикулярными некоторой прямой (оси вращения), пересекается по кругам с центрами на этой прямой. Цилиндр, конус, шар являются примерами тел вращения.

48. Многогранные углы. Многогранники.

Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей прямой. Полуплоскости называются гранями, а ограничивающая их прямая - ребром двугранного угла.

На рисунке 142 изображен двугранный угол с ребром а и гранями

Плоскость, перпендикулярная ребру двугранного угла, пересекает его грани по двум полупрямым. Угол, образованный этими полупрямыми, называется линейным углом двугранного угла. За меру двугранного угла принимается мера соответствующего ему линейного угла. Если через точку А ребра а двугранного угла провести плоскость у, перпендикулярную этому ребру, то она пересечет плоскости а и 0 по полупрямым линейный угол данного двугранного угла. Градусная мера этого линейного угла является градусной мерой двугранного угла. Мера двугранного угла не зависит от выбора линейного угла.

Трехгранным углом называется фигура, составленная из трех плоских углов Эти углы называются гранями трехгранного угла, а их стороны - ребрами. Общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы, образуемые гранями и их продолжениями, называются двугранными углами трехгранного угла.

Аналогично определяется понятие многогранного угла как фигуры, составленной из плоских углов Для многогранного угла определяются понятия граней, ребер и двугранных углов так же, как и для трехгранного угла.

Многогранником называют тело, поверхность которого состоит из конечного числа плоских многоугольников (рис. 145).

Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого многоугольника на его поверхности (рис. 145, а, б). Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника - выпуклые многоугольники. Стороны граней называются ребрами многогранника, а вершины - вершинами многогранника.

49. Призма. Параллелепипед. Куб.

Призмой называется многогранник» который состоит из двух плоских многоугольников, совмещаемых параллельным переносом, и всех отрезков» соединяющих соответствующие точки этих многоугольников. Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины, - боковыми ребрами призмы (рис. 146).

Так как параллельный перенос есть движение, то основания призмы равны. Так как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то

у призмы основания лежат в параллельных плоскостях. Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у призмы боковые ребра параллельны и равны.

На рисунке 147, а изображена четырехугольная прнзма Плоские многоугольники ABCD и совмещаются соответствующим параллельным переносом и являются основаниями призмы, а отрезки АА являются боковыми ребрами призмы. Основания призмы равны (параллельный перенос есть движение и переводит фигуру в равную ей фигуру, п. 79). Боковые ребра параллельны и равны.

Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. У каждого из этих параллелограммов две стороны являются соответствующими сторонами оснований, а две другие - соседними боковыми ребрами призмы.

На рисунке 147, с боковая поверхность призмы состоит из параллелограммов Полная поверхность состоит из оснований и указанных выше параллелограммов.

Высотой призмы называется расстояние между плоскостями ее оснований. Отрезок, который соединяет две вершины, не принадлежащие одной грани, называется диагональю призмы. Диагональным сечением призмы называется сечение ее плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

На рисунке 147, а изображена призма ее высота, одна из ее диагоналей. Сечение является одним из диагональных сечений этой призмы.

Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае прнзма называется

наклонной. Прямая призма называется правильной, если ее основаниями являются правильные многоугольники.

На рисунке 147, а изображена наклонная призма, а на рисунке 147, б - прямая, здесь ребро перпендикулярно основаниям призмы. На рисунке 148 изображены правильные призмы, у них основаниями являются соответственно правильный треугольник, квадрат, правильный шестиугольник.

Бели основания призмы - параллелограммы, то она называется параллелепипедом. У параллелепипеда все грани - параллелограммы. На рисунке 147, а изображен наклонный параллелепипед, а на рисунке 147, б - прямой.

Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. На рисунке 147, а грани противолежащие.

Можно доказать некоторые свойства параллелепипеда.

У параллелепипеда противоположные грани параллельны и равны.

Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

Точка пересечения диагоналей параллелепипеда является его центром симметрии.

Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани - прямоугольники.

Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.

Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами или измерениями. У прямоугольного параллелепипеда три линейных размера.

Для прямоугольного параллелепипеда верна такая теорема:

В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его линейных размеров.

Например, в кубе с ребром а диагонали равны:

50. Пирамида.

Пирамидой называется многогранник, который состоит из плоского многоугольника - основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину с точками основания (рис. 150). Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. На рисунке 150, а изображена пирамида SABCD. Четырехугольник ABCD - основание пирамиды, точка S - вершина пирамиды, отрезки SA, SB, SC и SD - ребра пирамиды.

Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. На рисунке 150, a SO - высота пирамиды.

Пирамида называется -угольной, если ее основанием является

Угольник. Треугольная пирамида называется также тетраэдром.

На рисунке 151, а изображена треугольная пирамида, или тетраэдр, на рисунке 151, б - четырехугольная, на рисунке 151, в - шестиугольная.

Плоскость, параллельная основанию пирамиды и пересекающая ее, отсекает подобную пирамиду.

Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. На рисунке 151 изображены правильные пирамиды. У правильной пирамиды боковые ребра равны; следовательно, боковые грани - равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.

По Т.3.4 плоскость а, параллельная плоскости 0 основания пирамиды и пересекающая пирамиду, отсекает от нее подобную пирамиду. Другая часть пирамиды представляет собой многогранник, который называется усеченной пирамидой. Грани усеченной пирамиды, лежащие в параллельных плоскостях называются основаниями усеченной пирамиды, остальные грани называются боковыми гранями. Основания усеченной пирамиды представляют собой подобные (более того, гомотетичные) многоугольники, боковые грани - трапеции. На рисунке 152 изображена усеченная пирамида

51. Правильные многогранники.

Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.

Существует пять типов правильных выпуклых многогранников (рис. 154): правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Про правильный тетраэдр и куб сказано раньше (п. 49, 50). В каждой вершине правильного тетраэдра и куба сходятся три ребра.

Грани октаэдра - правильные треугольники. В каждой его вершине сходятся по четыре ребра.

Грани додекаэдра - правильные пятиугольники. В каждой вершине сходятся по три ребра.

Грани икосаэдра - правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.

«Виды многогранников» - Правильные звездчатые многогранники. Додекаэдр. Малый звездчатый додекаэдр. Многогранники. Гексаэдр. Тела Платона. Призматоид. Пирамида. Икосаэдр. Октаэдр. Тело, ограниченное конечным числом плоскостей. Звездчатый октаэдр. Две грани. Закон взаимности. Математик. Тетраэдр.

«Геометрическое тело многогранник» - Многогранники. Призмы. Существование несоизмеримых величин. Пуанкаре. Грань. Измерение объемов. Грани параллелепипеда. Прямоугольный параллелепипед. Мы часто встречаем пирамиду на улице. Многогранник. Интересные факты. Александрийский маяк. Геометрические формы. Расстояние между плоскостями. Мемфис.

«Каскады многогранников» - Ребро куба. Ребро октаэдра. Куб и додекаэдр. Единичный тетраэдр. Додекаэдр и икосаэдр. Додекаэдр и тетраэдр. Октаэдр и икосаэдр. Многогранник. Правильный многогранник. Октаэдр и додекаэдр. Икосаэдр и октаэдр. Единичный икосаэдр. Тетраэдр и икосаэдр. Единичный додекаэдр. Октаэдр и тетраэдр. Куб и тетраэдр.

««Многогранники» стереометрия» - Многогранники в архитектуре. Сечение многогранников. Дайте название многограннику. Великая пирамида в Гизе. Платоновы тела. Исправить логическую цепочку. Многогранник. Историческая справка. Звездный час многогранников. Решение задач. Цели урока. «Игра со зрителями». Соответствуют ли геометрические фигуры и их названия.

«Звёздчатые формы многогранников» - Большой звездчатый додекаэдр. Многогранник, изображенный на рисунке. Звездчатые многогранники. Боковые ребра. Звездчатые кубооктаэдры. Звездчатый усеченный икосаэдр. Многогранник, полученный усечением звездчатого усеченного икосаэдра. Вершины большого звездчатого додекаэдра. Звездчатые икосаэдры. Большой додекаэдр.

«Сечение многогранника плоскостью» - Сечение многогранников. Многоугольники. Разрезы образовали пятиугольник. След секущей плоскости. Сечение. Найдём точку пересечения прямых. Плоскость. Построй сечение куба. Постройте сечение призмы. Находим точку. Призма. Методы построения сечений. Полученный шестиугольник. Сечение куба. Аксиоматический метод.

Всего в теме 29 презентаций